பாய்மங்கள் Notes 9th Science Lesson 3 Notes in Tamil

பாய்மங்கள் Notes 9th Science Lesson 3 Notes in Tamil

அறிமுகம்

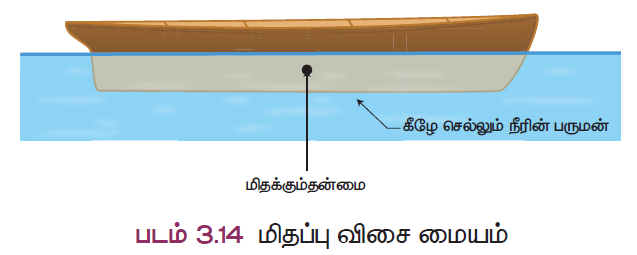
சிறிய இரும்பினாலான ஆணி ஒன்று நீரில் மூழ்குகின்றது. ஆனால் மிக அதிகமான நிறை கொண்ட கப்பல் ஒன்று நீரில் மிதக்கின்றது. விண்வெளி வீரர்கள் விண்வெளிப் பயணத்தின் போது சிறப்பு உடைகளை அணிகின்றனர். இவற்றிற்கெல்லாம் ஒரு பொதுவான காரணம் உண்டு. அதுதான் ‘அழுத்தம்’. திடப்பொருள்களின் மூலக்கூறுகளுக்கிடையே உள்ள விசையானது அதிகமாக உள்ளதால், அவற்றின் வடிவத்தையும் அளவையும் எளிதில் மாற்ற முடியாது. ஆனால், திரவத்திலும், வாயுக்களிலும் (கூட்டாக பாய்மரங்கள் என்று அழைக்கப்படுகின்றன) இவ்விசை கூறைவாக உள்ளதால் அவற்றின் வடிவத்தை எளிதில் மாற்றலாம். திடப்பொருள்களின் அழுத்தம் அதிகரிக்கும் போது, அவற்றின் சிறப்புப் பண்பினால் அவை இழுவிசைக்கு உட்பட்டு உருமாறுகின்றன அல்லது சிதைந்துவிடுகின்றன. ஆனால் பாய்மங்களில் அழுத்தம் அதிகரிக்கும் போது அவை சிதைவடையாமல் பாயும் தன்மையை அவ்வழுத்தம் அவற்றில் உண்டாக்குகிறது. திரவங்களுக்கும் வாயுக்களுக்கும் பொதுவான சில பண்புகள் இருந்தாலும், அவற்றிற்கென குறிப்பிட்ட சில சிறப்புப்பண்புகள் உள்ளன. வாயுக்களை எளிதாக அமுக்க இயலும்; ஆனால் திரவங்களை அமுக்க இயலாது. இவற்றைப்பற்றி கற்பதன் மூலம் அழுத்தத்தைப் பற்றி புரிந்து கொள்ளமுடியும். இப்பாடத்தில் பாய்மங்களின் அழுத்தம், அடர்த்தி மற்றும் அன்றாட வாழ்வில் அவற்றின் பயன்கள் ஆகியவற்றைப் பற்றி அறிந்து கொள்ள இருக்கிறீர்கள்.

அழுத்தம் மற்றும் உந்து விசை

குண்டூசி ஒன்றினை பலகையின் மீது அதன் தலைப்பகுதியின் மூலம் பொறுத்துவது கடினமாக இருக்கும். ஆனால், ஊசியின் கூர்மையான பகுதியினைக் கொண்டு பொறுத்துவது எளிது. ஏன்? பாலைவனத்தில் ஒட்டகம் எவ்வாறு விரைவாக ஓட முடிகிறது என்று வியந்ததுண்டா? பேருந்துகள் மற்றும் மோட்டார் வாகனங்களின் டயர்கள் ஏன் அகலமானதாக உள்ள? வெட்டுவதற்குப் பயன்படுத்தப்படும் கருவிகளின் முனைகள் ஏன் கூர்மையாக உள்ளன? இக்கேள்விகளுக்கு விடைதெரிந்து கொள்ள வேண்டுமெனில் ஒன்றோடு ஒன்று தொடர்புடைய இரு இயற்பியல் கருத்துக்களான அழுத்தம் மற்றும் உந்து விசையைப் பற்றி புரிந்து கொள்ள வேண்டும்.

மணற்பாங்கான பரப்பின் மீது நிற்கவும். உங்கள் கால்கள் மணலுக்குள் ஆழமாகச் செல்லும். அதே பரப்பின் மீது படுத்துப்பாருங்கள். என்ன நடக்கிறது? படுக்கும்போது, முன்புபோல் உடல் ஆழமாக மணலுக்குள் செல்லாது. ஏன்?

இந்த இரு நிகழ்வுகளிலும், மணல் மீது செயல்படும் விசையை ஏற்படுத்தும் உங்கள் உடலின் எடையானது மாறாமல் உள்ளது. பரப்பிற்குச் செங்குத்தாகச் செயல்படும் இந்த விசையானது உந்துவிசை எனப்படுகிறது. மணலில் நிற்கும்போது, செயல்படும் விசையானது கால்களின் பரப்பிற்குச் சமமான பரப்பளவில் செயல்படுகிறது. ஆனால் படுத்திருக்கும் நிலையில் அதே விசையானது உடலின் பரப்பளவிற்கு சமமான பரப்பில் செயல்படுகிறது. இப்பரப்பளவு கால்களின் பரப்பளவை விட அதிகமாகும். ஆகையால், உந்துவிசையின் விளைவாக தோன்றும் அழுத்தமானது, அது செயல்படும் பரப்பளவைச் சார்ந்ததாகும். எனவே, மணலில் நிற்கும்போது ஏற்படும் உந்துவிசையின் விளைவு படுக்கும்போது ஏற்படும் உந்து விசையின் விளைவை விட அதிகம்.

ஓரலகு பரப்பின் மீது செயல்படும் விசை அழுத்தம் எனப்படும். ஆகையால் ஓரலகு பரப்பின் மீது செயல்படும் உந்துவிசையே அழுத்தம் என்றும் கூறலாம்.

அழுத்தம் =

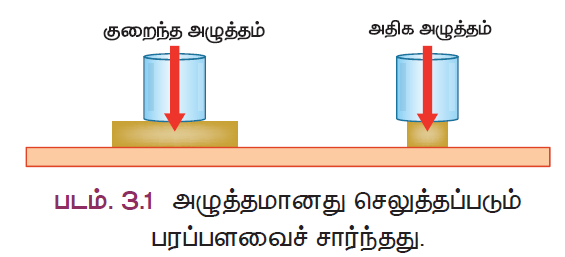
கொடுக்கப்பட்ட மாறா விசைக்கு, பரப்பளவு அதிகரிக்கும் போது அழுத்தம் கூறையும்; பரப்பளவு குறையும்போது அழுத்தம் அதிகரிக்கும். இதற்கான விளக்கத்தைப் படத்தில் பார்க்கலாம்.

S.I அலகுகளில், உந்துவிசையின் அலகு நியூட்டன் (N). அழுத்தத்தின் அலகு நியூட்டன் / சதுர மீட்டர் அல்லது நியூட்டன் மீட்டர்^-2 (Nm^-2). பிரான்ஸ் நாட்டு அறிவியல் அறிஞரான ப்ளைஸ் பாஸ்கல் என்பவரை சிறப்பிக்கும் வகையில் ஒரு நியூட்டன்/ சதுர மீட்டர் என்பது, ஒரு பாஸ்கல் (பிரான்ஸ் நாட்டு அறிவியல் அறிஞரான ப்ளைஸ் பாஸ்கல் என்பவரை சிறப்பிக்கும் வகையில் ஒரு நியூட்டன்/ சதுர மீட்டர் என்பது, ஒரு பாஸ்கல் (1Pa) என்று அழைக்கப்படுகிறது. 1 Pa = 1 Nm^-2.

ஒரு சிறிய ஆணி நமது உடலைத் துளைக்கும் போது வலியை உணர்கிறோம். ஆனால், சிலர் ஆணிப் படுக்கையில் படுத்தாலும், அவர்கள் உடலில் எந்தவித பாதிப்பும் ஏற்படாமல் இருக்கிறது. அது எப்படி? ஏனெனில், அவர்கள் உடல், ஆணியைத் தொடும் பரப்பானது அதிகமாக உள்ளது.

பாய்மங்களில் அழுத்தம்

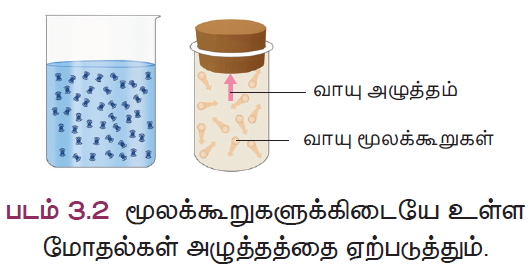
திரவங்கள் மற்றும் வாயுக்கள் இரண்டும் பொதுவாக பாய்மங்கள் என்று அழைக்கப்படுகின்றன. திடப்பொருள்களைப் போலவே பாய்மங்களுக்கும் எடை உண்டு. அதன் விளைவாக அவை அழுத்தத்தைக் கொண்டுள்ளன. ஒரு கொள்கலனில் நிரப்பப்படும் பாய்மமானது, அனைத்துத் திசைகளிலும், அனைத்துப் புள்ளிகளிலும் அழுத்தத்தை வெளிப்படுத்துகின்றது. பாய்மங்களில் உள்ள மூலக்கூறுகள் சீரற்ற மற்றும் வேகமான இயக்கத்தில் இருப்பதால், அனைத்துத் திசைகளிலும் சம அளவு நகரும் வாய்ப்பைப் பெற்றுள்ளன. இதனால், இரு பாய்மத்தினால் செலுத்தப்படும் அழுத்தமானது, ஒரு பொருளின் மீது அனைத்துத் திசைகளிலும் செயல்படுகிறது. இதனை படத்தில் காணலாம்.

பாய்மங்களின் அழுத்தத்தை கீழ்க்கண்டவாறு கணக்கிடலாம்.

பாய்ம அழுத்தம் =

நாம் முதலாவது திரவங்களால் ஏற்படும் அழுத்தத்தைப் பற்றிக் காண்போம். பின்னர், வாயுக்களினால் ஏற்படும் அழுத்தத்தைப் பற்றிக் காண்போம்.

திரவங்கள் ஏற்படுத்தும் அழுத்தம்

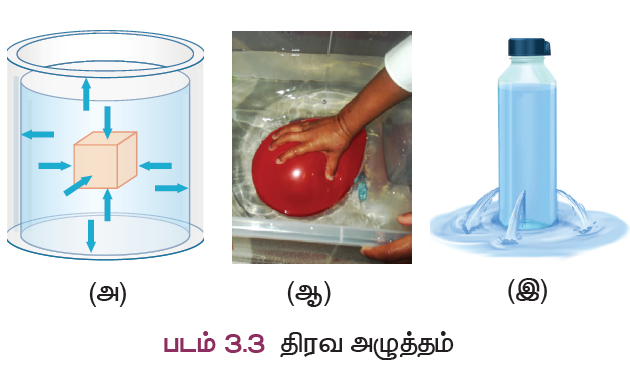
திரவங்களின் அழுத்தத்தினால், ஒரு திரவத்தில் மூழ்கியிருக்கும் பொருளின் மீதும், கொள்கலனின் சுவற்றின் மீதும் செயல்படும் விசையானது அவற்றின் மேற்பரப்பிற்குச் செங்குத்தாகவே செயல்படும். கொள்கலனின் அனைத்துத் திசைகளிலும் அழுத்தம் செயல்படுவதை படத்தில் காணலாம்.

காற்று நிரப்பப்பட்ட பலூன் ஒன்றினை நீரினுள் அழுத்தும் போது, அது உடனடியாக மேலெழும்பி, நீரின் மேல் மிதக்கும். இந்நிகழ்வு நீரில் (திரவங்களில்) மேல்நோக்கிய அழுத்தம் ஒன்று செயல்படுவதைக் குறிக்கிறது. இந்நிகழ்வை படத்தில் காணலாம்.

அதே போல், திரவங்களின் அழுத்தமானது பக்கவாட்டிலும் செயல்படுகிறது. பக்கவாட்டில் துளையிடப்பட்ட ஒரு பிளாஸ்டிக் பாட்டிலில் நீர் நிரப்பப்பட்டால், நீரானது துளைகளின் வழியே வெளியேறுவதை படத்தில் காணலாம். இதற்கு, திரவங்கள் கொள்கலனின் பக்கவாட்டுச் சுவர்களின் மீது ஏற்படுத்தும் அழுத்தம்தான் காரணமாகும்.

திரவ அழுத்தத்தினை நிர்ணயிக்கும் காரணிகள்

திரவங்களால் ஒரு புள்ளியில் செயல்படுத்தப்படும் அழுத்தமானது கீழ்க்கண்டவற்றால் நிர்ணயிக்கப்படுகிறது.

1. ஆழம் (h)
2. திரவத்தின் அடர்த்தி ()
3. புவியீர்ப்பு முடுக்கம் (g).

ஆழம் அதிகரிக்கும் போது அழுத்தம் அதிகரிக்கும். ஆனால், குறிப்பிட்ட ஆழத்தில் அழுத்தமானது திசையைப் பொறுத்து மாறாது.

திரவத்தம்பத்தினால் ஏற்படும் அழுத்தம்

ஒரு உயரமான கொள்கலனில் திரவம் நிரப்பப்படுகிறது எனக்கொள்வோம். அது ஒரு திரவத்தம்பத்தை அதனுள் ஏற்படுத்தும். அதன் குறுக்கு வெட்டுப்பரப்பளவு ‘A’ என்க. திரவத்தின் அடர்த்தி ‘’ மற்றும் திரவத்தம்பத்தின் உயரம் ‘h’ என்க. வேறுவிதமாகக் கூறினால், திரவத்தம்பத்தின் மேற்பரப்பில் இருந்து திரவத்தின் ஆழம் ‘h’ எனலாம். இதனை படத்தில் காணலாம்.

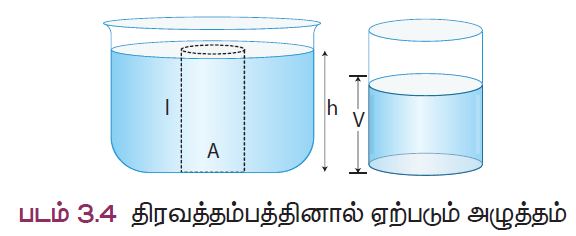
திரவத்தம்பத்தின் அடிப்பகுதியிலுள்ள உந்துவிசை (F) = திரவத்தின் எடை என்பதை அறிவோம். ஆகையால்.

F = mg (1)

திரவத்தின் நிறையானது திரவத்தின் பருமனை அதன் அடர்த்தியால் பெருக்கினால் கிடைக்கும்.

எனவே, நிறை m = V (2)

எனவே, திரவத்தின் பருமன்,

V = குறுக்குவெட்டுப் பரப்பளவு (A) x உயரம் (h) = Ah (3)

சமன்பாடு 3 ஐ, 2 ல் பிரதியிட,

நிறை, m = Ah (4)

சமன்பாடு 4 ஐ, 1 ல் பிரதியிட , F = Ahg

அழுத்தம் P =

எனவே, திரவத் தம்பத்தினால் ஏற்படும் அழுத்தம் P =

இதன்மூலம் ஒரு திரவத் தம்பத்திலுள்ள அழுத்தமானது, அத்திரவத் தம்பத்தின் ஆழம், அடர்த்தி மற்றும் புவியீர்ப்பு விசை ஆகியவற்றால் நிர்ணயிக்கப்படுகிறது என்பதை அறிய முடியும். ஆனால், இங்கு திரவத்தின் பரப்பளவு என்பது இடம் பெறவில்லை, எனவே, குறிப்பிட்ட ஆழத்தில் திரவத்தின் அழுத்தமானது, அந்தத் திரவத்தினைக் கொண்டுள்ள கொள்கலனின் வடிவத்தையோ அல்லது அதிலுள்ள திரவத்தின் அளவையோ பொறுத்ததல்ல. அது ஆழத்தை மட்டுமே பொறுத்தது.

வளிமண்டல அழுத்தம்

பூமியானது குறிப்பிட்ட உயரம் வரை (ஏறத்தாழ 300 கிமீ) காற்றால் சூழப்பட்டுள்ளது. இதனை புவியின் வளிமண்டலம் என்றழைக்கிறோம். காற்றானது இடத்தை அடைத்துக்கொள்ளும்; மேலும் அதற்கு எடை உள்ளது என்பதால் காற்றும் அழுத்தத்தை ஏற்படுத்தும். இந்த அழுத்தமானது வளிமண்டல அழுத்தம் எனப்படுகிறது. வளிமண்டல அழுத்தம் என்று குறிப்பிடும்போது கடல் மட்டத்தில் உள்ள அழுத்தத்தை நாம் குறிப்பிடுகிறோம்.

வளிமண்டலத்தின் அடர்த்தியானது, கடல் மட்டத்திலிருந்து உயரே செல்லும் போது குறைகிறது என்பதை படம் காட்டுகிறது. எனவே, மலைகளின் மேல் செல்லும்போது அழுத்தம் குறைகிறது. கடல் மட்டத்திற்கு கீழே, உதாரணமாக சுரங்கங்களுக்குள் செல்லும் போது அழுத்தம் அதிகரிக்கிறது.

• மனிதனின் நுரையீரல் கடல்மட்ட வளிமண்டல அழுத்தத்தில் (101.3kpa) சுவாசிப்பதற்கேற்ப தகுந்த தகவமைப்பைக் கொண்டுள்ளது. உயரமான மலைகளின் மேலே செல்லும்போது அழுத்தம் குறைவதால், மலையேறுபவர்களுக்கு உயிர்வாயு உருளை இணைந்த சிறப்பான சுவாசிக்கும் இயந்திரங்கள் தேவைப்படுகின்றன. அதுபோலவே, கடல் மட்டத்தைவிட அழுத்தம் அதிகமான சுரங்கங்களுக்குள் வேலை செய்பவர்களுக்கும் சிறப்பான சுவாசிக்கும் கருவிகள் தேவைப்படுகின்றன.

வளிமண்டல அழுத்தத்தை அளவிடுதல்

வளிமண்டல அழுத்தத்தை அளக்க காற்றழுத்தமானி என்னும் கருவி பயன்படுகிறது. இத்தாலிய இயற்பியலாளர், டாரிசெல்லி என்பவர் முதன்முதலாக ஒஆதரச காற்றழுத்தமானியை உருவாக்கினார். ஒரு முனை திறந்தும் ஒரு முனை மூடியும் உள்ள நீண்ட கண்ணாடிக் குழாயில் பாதரசம் நிரப்பப்பட்டு தலைகீழாக ஒரு கொள்கலனில் வைக்கபட்ட ஒரு அமைப்பை இது கொண்டுள்ளது. தலைகீழாகக் கவிழ்க்கும் போது , திறந்திருக்கும் முனையை கட்டை விரலால் மூடி, பாதரசம் உள்ள கொள்கலனில் கவிழ்க்க வேண்டும். (படம்). காற்றழுத்தமானி அதிலுள்ள பாதரத்தை வெளியில் உள்ள காற்றின் அழுத்தத்துடன் சமன்செய்து இயங்குகிறது. காற்றின் அழுத்தம் அதிகரிக்கும்போது, கொள்கலனில் உள்ள பாதரசம் கண்ணாடிக் குழாயினுள் தள்ளப்படுகிறது. காற்றின் அழுத்தம் குறையும் போது, குழாயினுள் உள்ள பாதரசம் வெளியேற்றப்படுகிறது. குழாயின் மூடிய முனைக்கும், உள்ளே உள்ள பாதரசத்திற்கும் இடையே காற்று இல்லாமல் வெற்றிடமாக உள்ளது. வெற்றிடம் எந்த அழுத்தத்தையும் ஏற்படுத்த இயலாது. ஆகையால் குழாயில் உள்ள பாதரசம் வளிமண்டலத்தின் அழுத்தத்தைத் துல்லியமாக வழங்குகிறது. இக்கருவியை ஆய்வகத்திலோ அல்லது வானிலை மையத்திலோ பயன்படுத்தலாம்.

ஒரு குறிப்பிட்ட நாளில், கடல் மட்ட அளவில் பாதரசத்தின் அழுத்தம் 760 மிமீ எனில், வளிமண்டல அழுத்தத்திற்குச் சமமான 760 மிமீ பாதரச தம்பத்தினால் ஏற்படும் அழுத்தத்தை இப்பொழுது கணக்கிடுவோம். (பாதரசத்தின் அடர்த்தி 13600 கிகிமீ^-3).

அழுத்தம் P = hg

= 760 x 10^-3 மீ x 13600 கிகிமீ^-3 x 9.8 கிகி வி^-2

= 1.013 x 10⁵ பாஸ்கல்

இதை வளிமண்டல அழுத்தம் (atm) என்கிறோம். இதற்கு பார் (bar) என்ற மற்றொரு அலகும் உள்ளது. இவ்வலகு அதிகமான அழுத்த மதிப்புகளைக் குறிப்பிடப் பயன்படுகிறது.

1 atm = 1.013 x 10⁵ பாஸ்கல்

1 பார் = 1 x 10⁵ பாஸ்கல்

ஆகையால் , 1 atm = 1.013 பார்

கிலோ பாஸ்கலின் அளவில் இதன் மதிப்பைக் கூறும் போது, வளிமண்டல அழுத்தமானது, 101.3 கிலோ பாஸ்கல் ஆகும்.

ஒவ்வொரு 1 மீ² பரப்பளவிலும் 1.013 கிலோ நியூட்டன் அளவுள்ள விசை செயல்படும் என்பதையே இது குறிக்கிறது.

அளவி மற்றும் தனிச்சுழி அழுத்தம்

நமது அன்றாட செயல்பாடுகள் அனைத்தும் வளிமண்டல அழுத்தத்தில் நடைபெறுகின்றன. இச்செயல்பாடுகள் அனைத்தும் இயல்பாக நடைபெறுவதால் நாம் அவற்றை உணர்வதுகூட கிடையாது. இரத்த அழுத்தம் மற்றும் வாகனங்களின் டயர் ட்யூப்களில் உள்ள அழுத்தம் ஆகியவை வளிமண்டல அழுத்தத்திற்கு அதிகமாக உள்ள அழுத்தத்தை குறிக்கின்றன. எனவே, தனிச்சுழி அழுத்தம் என்பது முழுமையான வெற்றிடத்தை பூஜ்யக் குறிப்பாகக் கொண்டு கணக்கிடப்படுவதாகும். அளவி அழுத்தம் என்பது வளிமண்டல அழுத்தத்தை பூஜ்யக் குறிப்பாகக் கொண்டு கணக்கிடப்படுவதாகும்.

வளிமண்டல அழுத்தத்தைவிட அதிகமான அழுத்தத்தைக் கணக்கிடும் போது,

தனிச்சுழி அழுத்தம் = வளிமண்டல அழுத்தம் + அளவி அழுத்தம்

வளிமண்டல அழுத்தத்தைவிட குறைவான அழுத்தத்தைக் கணக்கிடும் போது,

தனிச்சுழி அழுத்தன் = வளிமண்டல அழுத்தம் – அளவி அழுத்தம்

திரவத்தம்பம் அழுத்தத்தை ஏற்படுத்தும் என்பதை நாம் அறிவோம். எனவே, கடலின் உள்ளே அழுஹ்தம் அதிகமாக இருக்கும். அது வளிமண்டல அழுத்தத்தின் இருமடங்கைவிட அதிகமாக இருக்கும். இவ்வளவு அதிகமான அழுத்தத்தை நம்முடைய மென்மையான திசுக்களும், இரத்த நாளங்களும் தாங்கிக்கொள்ள இயலாது. எனவே, ஆழ்கடல் நீச்சல் வீரர்கள் சிறப்பான உடைகளை அணிந்தும், கருவிகள் கொண்டும் தங்களைப் பாதுகாத்துக் கொள்கின்றனர். (படம்)

• எரிபொருள் நிரப்பும் இடங்களில் வாகனங்களின் டயர் அழுத்தம் psi என்னும் அலகுகளில் குறிப்பிடப்படுகிறது. Psi என்னும் அலகு ஒரு அங்குலத்தில் (inch) செயல்படும் ஒரு பாஸ்கல் அழுத்தம் ஆகும். இது அழுத்தத்தை அளக்கும் ஒரு பழமையான முறையாகும்.

பாஸ்கல் விதி

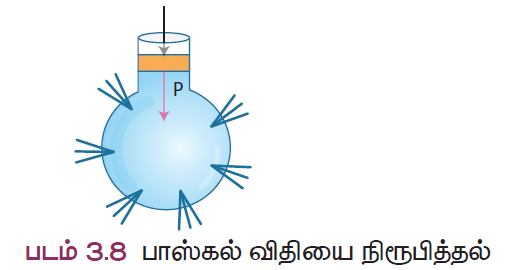
பாஸ்கல் தத்துவமானது பிரான்ஸ் நாட்டின் கணித மற்றும் இயற்பியல் மேதையான பிளைஸ் பாஸ்கலின் (Blaise Pascal, 1623 – 1662) நினைவாக பெயரிடப்பட்டுள்ளது. அழுத்தமுறா திரவங்களில் செயல்படும் புறவிசையானது, திரவங்களின் அனைத்துத் திசைகளிலும் சீராக கடத்தப்படும் என்பதை பாஸ்கல் விதி கூறுகிறது.

இவ்விதியை, பக்கவாட்டில் துளைகளைக் கொண்ட ஒரு கண்ணாடிக் குடுவையின் உதவியுடன் நிரூபித்துக் காட்டலாம். கண்ணாடிக் குடுவையை நீரினால் நிரப்பி, பிஸ்டனை அழுத்தவும். பிஸ்டனில் கொடுக்கப்படும் விசையானது செயல்படுவதன் மூலம், குடுவையில் உள்ள துளைகளின் வழியே நீர் பீறிட்டு வரு. பிஸ்டனில் கொடுக்கப்பட்ட விசையானது திரவத்தின் அனைத்துத் திசைகளிலும் சீராக கடத்தப்படுகிறது (படம்). இத்தத்துவமானது நாம் அன்றாட வாழ்வில் பயன்படுத்தும் பல்வேறு கருவிகளிலும் பயன்படுத்தப்படுகிறது.

நீரியல் அழுத்தி

இதுவரை உருவாக்கப்பட்ட முக்கியமான இயந்திரங்களுள் ஒன்றான நீரியல் அழுத்தியின் அடிப்படையாக பாஸ்கல் விதி அமைந்துள்ளது. படத்தில் காட்டப்பட்டுள்ள வெவ்வேறு குறுக்கு வெட்டுப் பரப்பைக் கொண்ட இரு உருளைகளை நீரியல் அழுத்தி கொண்டுள்ளது. இவ்விரு உருளைகளுடனும் ‘a’ மற்றும் ‘A’ என்ற குறுக்குவெட்டுப் பரப்பளவைக் கொண்ட பிஸ்டன்கள் இணைக்கப்பட்டுள்ளன. உயர்த்தப்பட வேண்டிய பொருளானது A என்ற பெரிய குறுக்கு வெட்டுப்பரப்பைக் கொண்ட பிஸ்டனின் மீது வைக்கப்பட்டுள்ளது. a என்ற குறுக்குவெட்டுப் பரப்பைக் கொண்ட பிஸ்டனின் மீது F₁ என்ற விசை அளிக்கப்படுகிறது. சிறிய பிஸ்டனின் மூலம் உருவாகும் அழுத்தமானது பெரிய பிஸ்டனுக்கு கடத்தப்படுகிறது. F₁ எனும் விசையை விட அதிகமான F₂ எனும் விசை பெரிய பிஸ்டன் மீது செயல்படுகிறது.

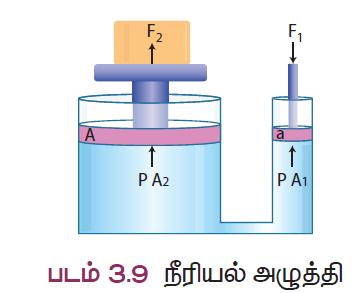
‘a’ எனும் பரப்பளவைக் கொண்ட சிறிய பிஸ்டனில் செயல்படும் அழுத்தம்

P = (1)

சிறிய பிஸ்டனில் செயல்படும் அழுத்தமும் பெரிய பிஸ்டனில் செயல்படும் அழுத்தமும் பாஸ்கல் விதியின்படி சமம். எனவே, பெரிய பிஸ்டனில் செயல்படும் அழுத்தமானது,

P = = (2)

கொடுக்கப்பட்ட இரு சமன்பாடுகளையும் ஒப்பிடும்போது,

= = அல்லது F₂ = F₁ x =

என்ற விகிதத்தின் மதிப்பு ஒன்றைவிட அதிகமாக உள்ளதால், பெரிய பிஸ்டனில் செயல்படும் விசையானது (F₂) சிறிய பிஸ்டனில் செயல்படும் விசையை (F₁) விட அதிகமாக உள்ளது. இவ்வாறு செயல்படும் நீரியல் அமைப்புகள் விசைப்பெருக்கிகள் (Force multipliers) எனப்படுகின்றன.

அடர்த்தி

ஒரு பொருளின் அடர்த்தியை அதன் ஓரலகு பருமனுக்கான நிறை என்று குறிப்பிடலாம்.

அடர்த்தியின் SI அலகு கிலோகிராம் / மீட்டர்³ அல்லது கிகி /மீ³. மேலும் கிராம் / சென்டிமீட்டர்³ (கி/மீ³) எனவும் இதனைக் குறிப்பிடலாம். அடர்த்திக்கான குறியீடு ரோ () எனப்படுகிறது.

ஒப்படர்த்தி

இரண்டு பொருள்களின் அடர்த்தியை ஒப்பிடுவதற்கு அவற்றின் நிறைகளைக் கண்டறிய வேண்டும். பெரும்பாலும் 4⁰C வெப்பநிலையில் நீரின் அடர்த்தியுடன் பொருள்களின் அடர்த்தியை ஒப்பிடுவதுதான் வழக்கமாக உள்ளது. ஏனெனில் , 4⁰C வெப்பநிலையில் நீரின் அடர்த்தி 1 கிசெமீ ³ ஆகும். ஒரு பொருளின் ஒப்படர்த்தி என்பது அப்பொருளின் அடர்த்தியை 4⁰C ல் நீரின் அடர்த்தியோடு ஒப்பிடுவதாகும். எனவே, ஒரு பொருளின் ஒப்படர்த்தி என்பது அப்பொருளின் அடர்த்திக்கும், 4⁰C வெப்பநிலையில் நீரின் அடர்த்திக்கும் உள்ள விகிதமென்று வரையறுக்கப்படுகிறது.

ஒப்படர்த்தி (R.D.) =

அடர்த்தி = என்பதால்,

ஒப்படர்த்தி =

ஆனால், பொருளின் பருமனும் நீரின் பருமனும் சமமாக உள்ளதால்,

ஒப்படர்த்தி =

எனவே, ஒரு பொருளின் ஒப்படர்த்தியானது குறிப்பிட்ட பருமன் அளவுள்ள அப்பொருளின் நிறைக்கும், 4⁰C வெப்பநிலையில் அதே பருமனைக் கொண்ட நீரின் நிறைக்கும் இடையே உள்ள விகிதத்தையும் குறிக்கிறது.

ஒப்படர்த்தியை அளவிடுதல்

பிக்நோமீட்டர் (Pycnometer) என்ற உபகரணத்தைக் கொண்டு ஒப்படர்த்தியை அளக்க முடியும். பிக்நோமீட்டர் என்பதற்கு அடர்த்திக் குடுவை (density bottle) என்ற மற்றொரு பெயரும் உண்டு. இக்குடுவையானது மெல்லிய துளையிடப்பட்ட அடைப்பானைக் கொண்டுள்ளது. இக்குடுவையை திரவத்தினால் நிரப்பி இந்த அடைப்பானால் மூடினால் குடுவையில் உள்ள உபரி திரவம் இதில் உள்ள துளையின் வழியே வெளியேறிவிடும். வெப்பநிலை சீராக இருக்குமானால், இக்குடுவை எப்போதும் ஒரே அளவு பருமனைக் கொண்ட திரவத்தை அதனுள் கொண்டிருக்கும் (அது எந்தத் திரவமாக இருந்தாலும்). எனவே, கொடுக்கப்பட்ட பொருளின் அடர்த்திக்கும் அதே பருமனுள்ள ஒப்பிடப்படும் பொருளின் அடர்த்திக்கும் இடையே உள்ள தகவு ஒப்படர்த்தியைக் குறிக்கிறது.

ஒப்பிடப்படும் பொருள் நீர் எனில் ஒப்படர்த்திக்குப் பதிலாக தன்னடர்த்தி (specific gravity) என்ற பதம் பயன்படுத்தப்படுகிறது.

மிதத்தல் மற்றும் மூழ்குதல்

ஒரு பொருளானது கொடுக்கப்பட்ட திரவத்தில் மூழ்குவதோ அல்லது மிதப்பதோ, குறிப்பிட்ட அந்த திரவத்தின் அடர்த்தியோடு அப்பொருளின் அடர்த்தியை ஒப்பிடுவதன் மூலம் நிர்ணயிக்கப்படுகிறது. திரவத்தின் அடர்த்தியை விட பொருளின் அடர்த்தி குறைவாக இருப்பின், அப்பொருளானது அத்திரவத்தில் மிதக்கும்.

எடுத்துக்காட்டாக, நீரைவிட அடர்த்தி குறைவான மரக்கட்டை நீரில் மிதக்கும். நீரை விட அதிக அடர்த்தி கொண்ட பொருள்கள், உதாரணமாக, கல்லானது நீரில் மூழ்கும்.

மிதத்தல் தத்துவத்தின் பயன்கள்

திரவமானி (Hydrometer)

ஒரு திரவத்தின் அடர்த்தியை அல்லது ஒப்படர்த்தியை நேரடியாக அளப்பதற்குப் பயன்படும் கருவி திரவமானி எனப்படும். மிதத்தல் தத்துவத்தின் அடிப்படையில் திரவமானிகள் வேலை செய்கின்றன. ஒரு திரவத்தில் மூழ்கியுள்ள திரவமானியின் பகுதியினால் வெளியேற்றப்பட்ட திரவத்தின் எடையானது திரவமானியின் எடைக்குச் சமமாக இருக்கும்.

திரவமானியானது அடிப்பகுதியில் கோள வடிவத்தினாலான குடுவையையும் மேற்பகுதியில் மெல்லிய குழாயையும் கொண்ட நீண்ட உருளை வடிவ தண்டைக் கொண்டுள்ளது. குழாயின் அடிப்பகுதியானது பாதரசம் அல்லது காரீயக் குண்டுகளால் நிரப்பப்பட்டுள்ளது. இது திரவமானியானது, மிதப்பதற்கும், திரவங்களில் செங்குத்தாக நிற்பதற்கும் உதவுகிறது. மேலே உள்ள மெல்லிய குழாயில் அளவீடுகள் உள்ளதால், திரவத்தின் ஒப்படர்த்தியை நேரடியாக அளக்கமுடிகிறது.

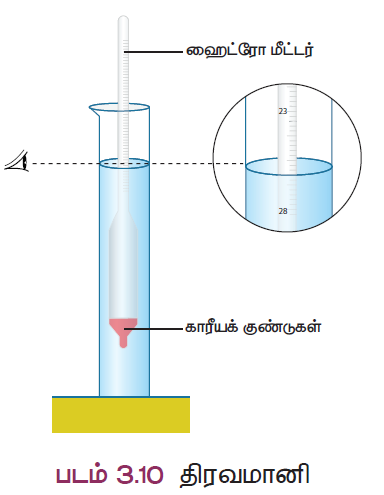
சோதிக்க வேண்டிய திரவத்தினை கண்ணாடிக் குடுவையில் நிரப்ப வேண்டும். திரவமானியை அத்திரவத்தில் மெதுவாக செலுத்தி, மிதக்கவிட வேண்டும். குழாயின் அளவீடுகள் திரவத்தின் மேற்பகுதியைத் தொடும் அளவு, திரவத்தின் ஒப்படர்த்தியாகும்.

திரவமானிகளைப் பல்வேறு பயன்பாட்டிற்கு ஏற்றபடி அளவுத்திருத்தம் (calibration) செய்து பாலின் அடர்த்தியைக் கண்டறியும் பால்மானி (Lactometer), சர்க்கரையின் அடர்த்தியைக் கண்டறியும் சர்க்கரைமானி (Saccharometer) மற்றும் சராயத்தின் அடர்த்தியைக் கணக்கிடும் சாராயமானி (Alcoholometer) போன்றவை உருவாக்கப்படுகின்றன.

பால்மானி

பால்மானி என்பது ஒருவகையான திரவமானியாகும். இது பாலின் தூய்மையைக் கண்டறியப் பயன்படும் ஒரு கருவியாகும். பாலின் தன்னடர்த்தி தத்துவத்தை அடிப்படையாகக் கொண்டு பால்மானி வேலை செய்கின்றது.

பால்மானியானது நீண்ட அளவிடப்பட்ட சோதனைக் குழாயுடன் உருளையான குமிழைக் கொண்டது. சோதனைக்குழாயின் மேல்பகுதியில் 15-ல் தொடங்கி அடிப்பகுதியில் 45 வரை அளவீடுகள் குறிக்கப்பட்டிருக்கும். இச்சோதனைக்குழாய் காற்றினால் நிரப்பப்பட்டிருக்கும். இக்காற்றைத்தான் பால்மானியை மிதக்கவைக்க உதவுகிறது. உருளையான குமிழினுள் நிரப்பப்பட்ட பாதரசமானது பால்மானியை பாலின் உள்ளே சரியான அளவு மூழ்கவும், செங்குத்தான நிலையில் மிதக்கவும் உதவுகிறது.

பால்மானியினுள்ளே வெப்பநிலைமானியும் இருக்கலாம். அது அடிப்பகுதியில் உள்ள குமிழ் முதல், அளவீடுகள் குறிக்கப்பட்ட மேற்பகுதி வரை அமைந்திருக்கும். 60⁰F வெப்பநிலையில்தான் பால்மானி மூலம் சரியான அளவீடுகளை அளக்கமுடியும். ஒரு பால்மானி பாலில் உள்ள அடர்த்தியான வெண்ணையின் அளவை அளவிடக்கூடியது. வெண்ணையின் அளவு அதிகமானால், பால்மானி பாலில் குறைவாக மிதக்கும். பால்மானி அளவிடும் சராசரியான பாலின் அளவீடு 32 ஆகும். பெரும்பாலும் பால் பதனிடும் இடங்களிலும், பால் பண்னைகளிலும் இவை பயன்படுத்தப்படுகின்றன.

மிதப்புத் தன்மை

ஒரு பொருள் , பாய்மங்களில் முழுமையாகவோ அல்லது ஓரளவிற்கோ மூழ்கியிருக்கும்போது, அப்பொருளானது சுற்றியுள்ள பாய்மத்தினால் மேல்நோக்கிய உந்துவிசையை உணர்கிறது என்று நாம் பார்த்தோம். மேலும் திரவங்களின் கீழ்பகுதிகளில் உள்ள அழுத்தம் மேல்பகுதியில் உள்ளதைவிட அதிகமாக உள்ளது என்பதையும் பார்த்தோம். இந்த அழுத்தவேறுபாடுதான் அப்பொருள் மீஹு ஒரு விசையைச் செலுத்தி அப்பொருளை மேல்நோக்கி உந்துகிறது. இந்த விசையை மிதப்பு விசை (buoyant force) என்றும் இந்நிகழ்வை மிதப்புத் தன்மை (buoyancy) என்றும் அழைக்கிறோம்.

பெரும்பாலான மிதக்கும் பொருள்கள் அதிக பருமனையும் குறைந்த அடர்த்தியையும் கொண்டிருக்கின்றன. ஒரு பொருளானது அது இடப்பெயர்ச்சி செய்த நீரின் எடையைவிட குறைவான எடையைக் கொண்டிருந்தால் (அடர்த்தி குறைவு) அத்தகைய பொருள்கள் நேர்மறையான மிதக்கும் தன்மையைக் கொண்டவை எனப்படுகின்றன. மாறாக ஒரு பொருளின் எடையானது அது இடப்பெயர்ச்சி செய்த நீரின் எடையை விட அதிகமாக இருந்தால் (அடர்த்தி அதிகம்) அப்பொருளின் மீது செயல்படும் மிதப்புவிடை குறைந்து அப்பொருள் மூழ்கிவிடும். இத்தகையை பொருள்கள் எதிர்மறையான மிதக்கும் தன்மையைக் கொண்டவை எனப்படும்.

• நன்னீரைவிட உப்புநீர் (கடல் நீர்) அதிகமான மிதப்பு விசையை ஏற்படுத்தும். ஏனெனில் மிதப்பு விசையானது பாய்மங்களின் பருமனைச் சார்ந்தது போல அதன் அடர்த்தியையும் சார்ந்துள்ளது.

கார்ட்டீடியன் மூழ்கி (Cartesian diver)

கார்ட்டீசியன் மூழ்கி சோதனையானது மிதப்புத் தன்மையின் தத்துவம் செயல்படும் விதத்தை விளக்குகிறது. இது களிமண்ணைக் கொண்டதொரு பேனா மூடியாகும். கார்டீசியன் மூழ்கியானது மிதப்பதற்குத் தேவையான போதிய அளவு திரவத்தினாலும், மீதிப்பகுதியில் காற்றினாலும் நிரப்பப்பட்டுள்ளது. கொள்கலனிலுள்ள நீரை அழுத்தும்போது அதிகமான உபரி நீர் அதனுள் சென்று, அடர்த்தி அதிகமாகி நீரினுள் மூழ்குகிறது.

ஆர்க்கிமிடிஸ் தத்துவம்

பாஸ்கல் விதியின் விளைவே ஆர்க்கிமிடிஸின் தத்துவமாகும். வரலாற்றுக் குறிப்புகளின் படி, குளியல் தொட்டியில் அமர்ந்திருக்கும் போது தனது எடையில் ஏற்பட்ட வெளிப்படையான இழப்பைக் கவனித்தபிறகு ‘நீர்நிலை சமநிலையின்’ (hydrostatic balance) தத்துவத்தை ஆர்க்கிமிடிஸ் உருவாக்கினார். அவர் இந்தத் தத்துவத்தைக் கண்டுபிடித்தவுடன் ‘யுரேகா’ என்று அலறிக்கொண்டே குளியல் தொட்டியிலிருந்து வெளியே ஓடினார் என்று கூறப்படுகிறது. “ஒரு பொருளானது பாய்மங்களில் மூழ்கும் போது, அப்பொருள் இடப்பெயர்ச்சி செய்த பாய்மத்தின் எடைக்குச் சமமான செங்குத்தான மிதப்பு விசையை அது உணரும்” என்று ஆர்க்கிமிடிஸ் தத்துவம் கூறுகிறது.

ஒருபொருள் முழுமையாகவோ பகுதியாகவோ ஓய்வுநிலையில் உள்ள பாய்மத்தில் மூழ்கும்போது, அப்பொருள் இடப்பெயர்ச்சி செய்த பாய்மத்தின் எடைக்குச் சமமான மேல்நோக்கு விசையை உணரும். இந்த மேல்நோக்கு விசையினால் பொருள் தன் எடையின் ஒரு பகுதியை இழக்கிறது. எடையில் ஏற்பட்ட இந்த இழப்பு மேல்நோக்கு விசைக்குச் சமமாக உள்ளது.

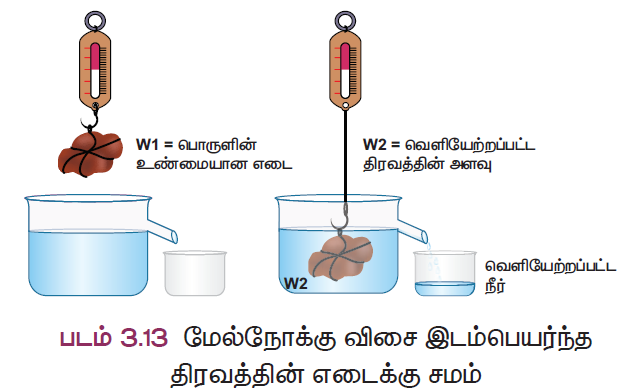
எனவே, பொருளொன்று முழுமையாகவோ அல்லது பகுதியாகவோ பாய்மங்களில் மூழ்கும் போது,

மேல் நோக்கு விசை = இடப்பெயர்ச்சி செய்யப்பட்ட பாய்மத்தின் எடை

= பொருளின் தோற்ற எடை இழப்பு

பொருளின் தோற்ற எடை இழப்பு = காற்றில் பொருளின் எடை – மேல் நோக்கு விசை (இடப்பெயர்ச்சி செய்யப்பட்ட நீரின் எடை)

மிதத்தல் விதிகள்

மிதத்தல் விதிகளாவன:

1. பாய்மம் ஒன்றின் மீது மிதக்கும் பொருளொன்றின் எடையானது, அப்பொருளினால் வெளியேற்றப்பட்ட பாய்மத்தின் எடைக்குச் சமமாகும்.
2. மிதக்கும் பொருளின் ஈர்ப்பு மையமும் மிதப்பு விசையின் மையமும் ஒரே நேர்கோட்டில் அமையும்.

மிதப்புவிசை செயல்படும் புள்ளியே மிதப்பு விசை மையம் எனப்படுகிறது. இது படத்தில் காட்டப்பட்டுள்ளது.