இயக்க விதிகள் Notes 10th Science Lesson 1 Notes in Tamil

இயக்க விதிகள் Notes 10th Science Lesson 1 Notes in Tamil

அறிமுகம்:

மனிதர் தம்மைச் சுற்றியுள்ளவைகளை கூர்ந்து நோக்குவதில் மிகுந்த ஆர்வம் உடையவராவர். நம்மை சுற்றியுள்ள பொருள்கள் அனைத்தும் ஒன்றையொன்று சார்ந்து உள்ளன. அவற்றில் சில ஓய்வு நிலையிலும், சில இயங்கும் நிலையிலும் உள்ளன. ஓய்வும் இயக்கமும் ஒன்றுடன் ஒன்று தொடர்புடையவை.

முந்தைய வகுப்புகளில் நாம் இயக்கத்தின் பல்வேறு வகைகளான நேர்க்கோட்டு இயக்கம், வட்ட இயக்கம், அலைவு இயக்கம் போன்றவற்றை கற்றறிந்தோம். இதுவரை இயக்கத்தின் கூறுகளான இடப்பெயர்ச்சி, திசைவேகம், மற்றும் முடுக்கம் இவற்றைப் பற்றி அறிந்தோம். இப்போது இந்த பாடத்தில் இயக்கத்திற்கான காரணத்தை ஆய்ந்தறிவோம்.

ஓய்வில் உள்ள ஒரு பொருளை இயக்கத்திற்கு மாற்ற உதவுவது எது? இயக்கத்தில் உள்ள ஒரு பொருள் ஓய்வுநிலைக்கு வருவதற்கு காரணம் என்ன? இயங்கும் பொருளை வேகமாக இயக்குவதற்கும், வேகத்தை குறைக்கவும் எது தேவைப்படுகிறது? நகரும் பொருளின் திசையினை மாற்ற உதவுவது எது?

மேற்கண்ட அனைத்து வினாக்களுக்கும் ஒரே விடை “விசை” என்பதாகும்.

பொதுவாக விசை என்பது “தள்ளுதல்” அல்லது “இழுத்தல்” என்ற பதத்திலேயே பொருள் கொள்ளப்படுகிறது.

ஓய்வு நிலையில் உள்ள பொருளை இயக்க அல்லது இயக்க நிலையில் உள்ள பொருளை ஓய்வுநிலைக்குக் கொண்டுவர விசை தேவைப்படுகிறது. மேலும் இயக்கத்தில் உள்ள பொருளின் திசைவேகத்தை அதிகரிக்கவோ அல்லது குறைக்கவோ, அதன் திசையினை மாற்றவோ விசை என்பது தேவைப்படுகிறது.

அறிவியல் பூர்வமாக விசை என்பதை சர்.ஐசக்.நியூட்டனின் மூன்று இயக்க விதிகள் மூலம் விளக்க இயலும். இவ்விதிகள் மூலம் பொருளின் இயக்கத்தினை தெளிவாகப் புரிந்து கொள்வதுடன், இயக்கத்தில் உள்ள பொருளின் மீது செயல்படும் விசை மதிப்பைக் கொண்டு, அப்பொருள் எவ்வாறு இயங்கப்போகின்றது? என்பதை முன்பே தெரிந்து கொள்ளவும் உதவியாக உள்ளது. நியூட்டனின் இயக்க விதிகளுக்கு முன் விசை மற்றும் இயக்கம் பற்றிய பல்வேறு விதமான கருத்துக்கள் இருந்தன. இப்பாடத்தில் அக்கருத்துக்கள் பற்றியும், விசை மற்றும் இயக்கம் பற்றிய நியூட்டனின் மூன்று இயக்க விதிகளையும் அறிந்து கொள்வோம்.

இயந்திரவியல்: விசையின் செயல்பாட்டால் பொருள் மீது ஏற்படும் விளைவுகளை பற்றி பயிலும் அறிவியல் பாடம் இயந்திரவியல் ஆகும். இது இரண்டு பிரிவுகளாகப் பிரிக்கப்பட்டுள்ளது. அவை நிலையியல் மற்றும் இயங்கியல் ஆகும்.

நிலையியல்: விசையின் செயல்பாட்டால் ஓய்வு நிலையிலுள்ள பொருள் மீது ஏற்படும் விளைவுகளைப் பற்றி அறியும் அறிவியல் நிலையியல் ஆகும்.

இயங்கியல்: விசையின் செயல்பாட்டால் இயக்க நிலையிலுள்ள பொருள் மீது ஏற்படும் விளைவுகளைப் பற்றி அறியும் அறிவியல் இயக்கவியல் ஆகும். இது மேலும் இரு பிரிவுகளாக கீழ்கண்டவாறு பிரிக்கப்பட்டுள்ளது.

இயக்கவியல்: இயக்கவியல் என்பது இயக்கத்தை ஏற்படுத்தும் விசையினைக் கருத்தில் கொள்ளாமல் இயக்கத்தினை மட்டுமே விளக்குவது இயக்கவியல் ஆகும்.

இயக்கவிசையியல்: பொருளின் இயக்கத்தையும், அதற்குக் காரணமான விசை பற்றியும் விளக்குவது இயக்க விசையியல் ஆகும்.

விசை மற்றும் இயக்கம்:

அரிஸ்டாட்டில் கிரேக்க நாட்டில் வாழ்ந்த ஒரு சிறந்த அறிவியல் மற்றும் தத்துவ அறிஞர் ஆவார். அவரது கூற்றுப்படி, இயங்குகின்ற பொருள்கள் யாவும் தாமாகவே இயற்கையான தத்துமது ஓய்வுநிலைக்கு வந்து சேரும். அவற்றினை ஓய்வு நிலைக்கு கொண்டு வரபுறவிசை எதுவும் தேவையில்லை எனக் கூறினார். இவ்வாறு இயங்கும் பொருட்களின் இயக்கத்தினை “இயற்கையான இயக்கம்” (விசை சார்பற்ற இயக்கம்) என வரையறுத்தார். அவ்வாறு இல்லாமல், இயங்கும் பொருட்களை ஓய்வுநிலைக்குக் கொண்டு வர புறவிசை தேவைப்படும் எனில், அவ்வகை இயக்கத்தினை “இயற்கைக்கு மாறான இயக்கம்” (விசை சார்பு இயக்கம்) என வரையறுத்தார். மேலும் இரு வேறு நிறை கொண்ட பொருள்கள் சம உயரத்தில் இருந்து விழும்போது, அதிக நிறை கொண்ட பொருள் வெகு வேகமாக விழும் என்றுரைத்தார்.

அறிவியலறிஞர் கலிலியோ விசை, நிலைமம் மற்றும் இயக்கம் பற்றி கீழ்கண்டவாறு விளக்கினார்.

1. இயற்கையில் உள்ள புவிசார் பொருள்கள் யாவும் தத்தமது இயல்பான ஓய்வு நிலையிலோ அல்லது சீரான இயக்க நிலையிலோ தொடர்ந்து இருக்கும்.
2. புறவிசை ஏதும் செயல்படாத வரை பொருள்கள் யாவும் தத்தமது முந்தைய நிலையிலேயே தொடர்ந்து இருக்கும்.
3. பொருளின் மீது விசையின் தாக்கம் இருக்கும்போது, தம் நிலை மாற்றத்தினை தவிர்க்க முயலும் தன்மை அதன் நிலைமம் எனப்படும்.
4. வெற்றிடத்தில் வெவ்வேறு நிறை கொண்ட பொருள்கள் யாவும் ஒரே உயரத்தில் இருந்து விழும்போது, அவை ஒரே நேரத்தில் தரையை வந்தடையும்.

நிலைமம்:

நாம் பேருந்திலோ மகிழுந்திலோ பயணம் செய்யும் போது, திடீரென அவை நிறுத்தப்படும் போது, நமது உடல் முன்னோக்கி சாய்கின்றது. ஓய்வு நிலையில் உள்ள பேருந்து, திடீரென நகரும் போது, உள்ளிருக்கும் நாம் பின்னே சாய்கின்றோம்.

தொடர்ந்து இயங்கி கொண்டுள்ள வாகனத்தில் திடீரென வேகத்தடை ஏற்படும்போது பேருந்து நின்றுவிட்டாலும், பயணியர் தொடர்ந்து இயக்க நிலையிலேயே இருக்க முயற்சிப்பதால் முன்னோக்கி விழுகின்றனர். அதேபோல் ஓய்வு நிலையில் உள்ள பேருந்து, திடீரென நகர ஆரம்பிக்கும் பொழுது, அவற்றுடன் இணைந்த பயணியர், தொடர்ந்து ஓய்வில் இருக்க முயல்கின்றனர். எனவே பேருந்து நகர்ந்தாலும், அவர்கள் தமது பழைய நிலையை தக்க வைக்க பின்னோக்கி சாய்கின்றனர்.

ஒவ்வொரு பொருளும் தன் மீது சமன் செய்யப்படாத புற விசை ஏதும் செயல்படாத வரையில், தமது ஓய்வு நிலையையோ, அல்லது சென்று கொண்டிருக்கும் நேர்க்கோட்டு இயக்க நிலையையோ மாற்றுவதை எதிர்க்கும் தன்மை “நிலைமம்” என்றழைக்கப்படுகிறது.

இச்செயல்பாட்டில் காகித அட்டை நகர்ந்தாலும், நாணயமானது தொடர்ந்து தமது ஓய்வின் நிலைப்புத் தன்மையை நீட்டிக்க முயற்சிக்கிறது. இந்த ஓய்விற்கான நிலைமப் பண்பினால், அட்டை நகர்ந்தவுடன் புவி ஈர்ப்பு விசையினால் நாணயம் குவளையில் விழுகிறது.

நிலைமத்தின் வகைகள்:

அ) ஓய்வில் நிலைமம்: நிலையாக உள்ள ஒவ்வொரு பொருளும் தமது ஓய்வு நிலை மாற்றத்தை எதிர்க்கும் பண்பு ஓய்வில் நிலைமம் எனப்படும்.

ஆ) இயக்கத்தில் நிலைமம்: இயக்க நிலையில் உள்ள பொருள், தமது இயக்க நிலை மாற்றத்தை எதிர்க்கும் பண்பு இயக்கத்தில் நிலைமம் எனப்படும்.

இ) திசையில் நிலைமம்: இயக்க நிலையில் உள்ள பொருள், இயங்கும் திசையில் இருந்து மாறாது, திசை மாற்றத்தினை எதிர்க்கும் பண்பு திசையில் நிலைமம் எனப்படும்.

நிலைமத்திற்கான எடுத்துக்காட்டுகள்:

• நீளம் தாண்டுதல் போட்டியில் உள்ள போட்டியாளர் நீண்ட தூரம் தாண்டுவதற்காக, தாம் தாண்டும் முன் சிறிது தூரம் ஓடுவதற்கு காரணம் இயக்கத்திற்கான நிலைமம் ஆகும்.
• ஓடும் மகிழுந்து வளைபாதையில் செல்லும் போது பயணியர், ஒரு பக்கமாக சாயக் காரணம் திசைக்கான நிலைமம் ஆகும்.
• கிளைகளை உலுக்கிய பின் மரத்திலிருந்து கீழே விழும் இலைகள், பழுத்தபின் விழும் பழங்கள் இவை யாவும் ஓய்விற்கான நிலைமத்திற்கு எடுத்துகாட்டாகும்.

இயக்கத்தில் நிலைமம்

நேர்கோட்டு உந்தம் (Linear Momentum):

திசைவேகமோ, நிறையோ அதிகமானால் விசையின் தாக்கம் அதிகமாகும். விசையின் விளைவானது திசைவேகத்தையும், நிறையினையும் சார்ந்து அமைகிறது. ஒரு பொருள் மீது செயல்படும் விசையின் தாக்கத்தை நேரகோட்டு உந்தத்தின் மூலம் அளவிடலாம்.

இயங்கும் பொருளின் நிறை மற்றும் திசைவேகத்தின் பெருக்கற்பலன் உந்தம் எனப்படும். இதன் திசையானது பொருளின் திசைவேக திசையிலேயே அமையும். இது ஒரு வெக்டார் அளவாகும்.

உந்தம் (p) = நிறை (m) x திசைவேகம் (v)

P = mv

விசையின் எண் மதிப்பானது உந்தத்தால் அளவிடப்படுகிறது. இதன் SI அலகு கிகி மீவி^-1, CGS அலகு கி செ.மீ வி^-1 ஆகும்.

நியூட்டனின் இயக்க விதிகள்:

நியூட்டனின் முதல் விதி:

ஒவ்வொரு பொருளும் புறவிசை ஏதும் செயல்படாத வரையில், தமது ஓய்வு நிலையிலோ அல்லது சீராக இயங்கிக் கொண்டிருக்கும் நேர்க்கோட்டு நிலையிலோ தொடர்ந்து இருக்கும். இவ்விதி விசையினை வரையறுக்கிறது. அது மட்டுமின்றி, பொருட்களின் நிலைமத்தையும் விளக்குகிறது.

விசை:

விசை என்பது “இழுத்தல்”அல்லது “தள்ளுதல்” என்ற புறச்செயல் வடிவம் ஆகும். இதை கீழ்கண்டவாறு விளக்கலாம்.

1. ஓய்வில் உள்ள பொருளை இயக்குவதற்கு அல்லது இயக்க முயற்சிப்பதற்கான செயல்.
2. இயங்கி கொண்டிருக்கும் பொருளை நிறுத்த அல்லது நிறுத்த முயற்சிப்பதற்கான செயல்.
3. இயங்கி கொண்டிருக்கும் பொருளின் திசையினை மாற்ற அல்லது மாற்ற முயற்சிக்கின்ற செயல் ஆகும்.

விசையானது எண்மதிப்பும் திசையும் கொண்ட ஒரு வெக்டார் அளவாகும்.

விசையின் வகைகள்:

விசைகளை, அவை செயல்படும் திசை சார்ந்து கீழ்கண்டவாறு வகைப்படுத்தலாம்.

அ) ஓத்த இணைவிசைகள்: இரண்டு அல்லது இரண்டிற்கு மேற்பட்ட சமமான அல்லது சமமற்ற விசைகள், ஒரே திசையில் ஒரு பொருள் மீது இணையாகச் செயல்பட்டால் அவை ஒத்த இணைவிசைகள் என்றழைக்கப்படுகின்றன.

ஆ) மாறுபட்ட இணைவிசைகள்: இரண்டு அல்லது இரண்டிற்கு மேற்பட்ட சமமான அல்லது சமமற்ற விசைகள், எதிர் எதிர் திசையில் ஒரு பொருள் மீது இணையாகச் செயல்பட்டால் அவை மாறுபட்ட இணைவிசைகள் என்றழைக்கப்படுகின்றன.

இவ்விசைகளின் செயல்பாடுகளை மேலும் அறியலாம்.

தொகுபயன் விசை (Resultant Force):

ஒரு பொருள் மீது பல்வேறு விசைகள் செயல்படும்போது, அவற்றின் மொத்த விளைவை ஏற்படுத்தும் ஒரு தனித்த விசை “தொகுபயன் விசை” என்றழைக்கப்படுகிறது. இதன் மதிப்பு, செயல்படும் அனைத்து விசைகளின் வெக்டார் கூடுதலுக்குச் (விசைகளின் எண்மதிப்பு மற்றும் திசை ஆகியவற்றின் கூடுதல்) சமமாகும்.

தொகுபயன் விசையின் மதிப்பு சுழி எனில் பொருள் சமநிலையில் உள்ளதென அறியலாம். இவ்விசைகள் சமன் செய்யப்பட்ட விசைகள் எனப்படும். தொகுபயன் விசை மதிப்பு சுழியில்லை எனில், அவை பொருட்களின் இயக்கத்திற்கு காரணமாக அமைகின்றன. இது சமன் செய்யப்படாத விசைகள் எனப்படும்.

எ.கா: கிணற்றில் இருந்து நீர் எடுக்க செயல்படும் விசை, நெம்புகோலின் மீது செயல்படும் விசை, தராசுத்தட்டுகளில் செயல்படும் விசை முதலியன சமன் செய்யப்படாத விசைகளுக்கு எடுத்துக்காட்டுகள் ஆகும்.

தொகுபயன் விசைக்கு சமமான, ஆனால் எதிர் திசையில் செயல்படும் ஒரு விசையானது, பொருட்களை சம நிலைக்கு கொண்டுவர உதவுகிறது. இவ்விசையை “எதிர்சமனி”(Equilibrant) என்று அழைக்கப்படுகிறது.

விசையின் சுழல் விளைவு:

கதவுகளில் கைப்பிடி எந்த இடத்தில் பொருந்தியுள்ளது? மற்ற இடத்தில் வைக்காமல் ஏன் எப்போதும் கதவுவின் விளிம்பருகில் அவை பொருத்தப்பட்டுள்ளன? கதவினை, விளிம்புகளில் பிடித்து இழுப்பது அல்லது தள்ளுவது எளிதானதா? அல்லது சுவரின் இணைப்பு கீல் (Hinges) பகுதியின் அருகில் பிடித்து இழுப்பது அல்லது தள்ளுவது எளிதானதா?

கதவினை திறக்க அல்லது மூட, விசையினை விளிம்புகளில் செலுத்துவது எளிதானதாகும். கதவின் இணைப்பு அச்சிலிருந்து விளிம்பானது தொலை தூரத்தில் உள்ளது. எனவே அங்கு செயல்படும் விசை அதிக சுழல் விளைவினை ஏற்படுத்துகிறது. கதவில் உள்ள நிலையான இணைப்பு அச்சு, “சுழல் அச்சு” (Axis of rotation) என்றழைக்கப்படும்.

விசையின் செயல்பாடுகள்

விசை செயல்பாடு	படம்	தொகுபயன் விசை (Fதொகு) மதிப்பு
ஒத்த இணை விசைகள் ஒரே திசையில் செயல்பட்டால்		Fதொகு = F1 + F2
சமமற்ற மதிப்புகள் கொண்ட இணை விசைகள் எதிரெதிர் திசையில் செயல்பட்டால்		Fதொகு = F1 – F2 (F1 > F2 எனில்) Fதொகு = F2 – F2 (F2 > F1 (எனில்) Fதொகு விசையானது அதிக எண் மதிப்புடைய விசையின் திசையில் நகரும்
சமமான விசைகள் எதிர்எதிர் திசையில் ஒரே நேரத்தில் நேர்க்கோட்டில் செயல்பட்டால்		Fதொகு = F1 – F2 Fதொகு = ஏனெனில் (F1 = F2)

விசைகளின் தொகுபயன் விளைவு

தண்டொன்றின் ஒரு முனையை தரையிலோ அல்லது சுவரிலோ நிலையாக பொருத்தி, மறுமுனையில் தண்டின் தொடுகோட்டின் வழியே விசை செயல்படுத்தப்பட்டால், தண்டானது நிலைப்புள்ளியை மையமாக வைத்து சுழலும், இப்புள்ளி “சுழற்புள்ளி” (Point of rotation) எனப்படும்.

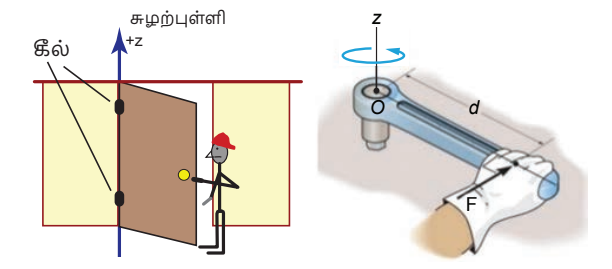
விசையின் சுழல் விளைவு

விசையின் திருப்புத்திறன்:

விசையானது ஒரு புள்ளியில் அல்லது ஒரு அச்சில் ஏற்படுத்தும் சுழற் விளைவினை அதன் திருப்புத்திறன் மதிப்பின் மூலம் அளவிடலாம்.

ஒரு புள்ளியில் மீது செயல்படும் விசையின் திருப்புத்திறன் τ ஆனது, விசையின் எண் மதிப்பு F-ற்கும், நிலையான புள்ளி மற்றும் விசை செயல்படும் அச்சிற்கும் இடையே உள்ள செங்குத்து தொலைவு d க்கும், உள்ள பெருக்கற் பலனைக் கொண்டு அளவிடப்படுகிறது.

Τ = F x d

இது ஒரு வெக்டார் அளவாகும். இதன் திசையானது விசை செயல்படும் அச்சின் திசை மற்றும் தொலைவின் தளத்திற்கு, செங்குத்து திசையில் இருக்கும். இதன் SI அலகு நியூட்டன் மீட்டர் (N m) ஆகும்.

இரட்டை (Couple): இரு சமமான இணை விசைகள் ஒரே நேரத்தில் ஒரு பொருளின் இரு வேறு புள்ளிகளின் மீது எதிர் எதிர் திசையில் செயல்பட்டால், அவை “இரட்டை விசைகள்” அல்லது “இரட்டை” என்றழைக்கப்படும். அவை ஒரே நேர்க்கோட்டில் செயல்படாது.

இரட்டைகளின் தொகுபயன்விசை மதிப்பு சுழியாதலால் இவை நேர்க்கோட்டு இயக்கதினை ஏற்படுத்தாது. ஆனால் சுழல் விளைவினை ஏற்படுத்தும். இதை இரட்டைகளின் திருப்புத்திறன் என்றழைக்கிறோம்.

எ.கா.நீர் குழாய் திறத்தல் மற்றும் மூடுதல், திருகின் சுழற்சி, பம்பரத்தின் சுழற்சி முதலானவை.

இரட்டையின் சுழற்விளைவு, அதன் திருப்புத் திறன் மதிப்பு கொண்டு அளவிடப்படுகிறது. இம்மதிப்பு எதெனும் ஒரு விசையின் எண்மதிப்பு மற்றும் இணை விசைகளுக்கு இடையே உள்ள செங்குத்து தொலைவு, இவைகளின் பெருகற்பலனுக்கு சமமாகும்.

இரட்டையின் திருப்புத்திறன் (M) = விசையின் எண் மதிப்பு (F) x இணை விசைகளுக்கு இடையே உள்ள செங்குத்து தொலைவு (S)

M = F x S

இதன் SI அலகு நியூட்டன் மீ, CGS அலகு முறையில் டைன் செ.மீ ஆகும். விசையின் திருப்புத்திறன் ஒரு வெக்டார் அளவாகும். திருப்புத்திறனின் திசை, பொருட்களின் சுழற்சி வலஞ்சுழியாக இருப்பின் எதிர்க்குறியாகவும், இடஞ்சுழியாக இருப்பின் நேர்க்குறியாகவும் கொள்ளப்படுவது மரபாகும். இது (a) மற்றும் (b) ல் காட்டப்பட்டுள்ளது.

(a) மற்றும் (b)

விசையின் திருப்புத்திறன் செயல்படும் சில எடுத்துக்காட்டுகள்:

1. பற்சக்கரங்கள் (Gears):

பற்சக்கரங்கள் வட்டப்பரப்பின் விளிம்புகளில் பல் போன்று மாற்றம் செய்யப்பட்ட அமைப்புகள் ஆகும். பற்சக்கரங்கள் மூலம் திருப்புவிசையினை மாற்றி இயங்குகின்ற வாகனசக்கரங்களின் சுழற்சி வேகத்தை மாற்றலாம். மேலும் திறனை கடத்துவதற்கும் பற்சக்கரங்கள் உதவுகின்றன.

1. ஏற்றப்பலகை (Seesaw Play):

நீங்கள் ஏற்றப்பலகை விளையாட்டினை விளையாடி இருப்பீர்கள். அதில் அமர்ந்துள்ள எடை அதிகமான ஒருவர், மற்றொருவரை எளிதில் தூக்குகிறார். ஏடை அதிகமான நபர் பலகையின் ஆதாரப்புள்ளியினை நோக்கி நகரும் போது, விசை செயல்படும் தூரம் குறைந்து, திருப்புவிசையின் செயல்பாடு குறைகிறது. இது எடை குறைவான நபரானவர், எடை அதிகமான நபரை தூக்க வழி வகை செய்கிறது.

1. திருப்புச்சக்கரம் (Steering Wheel) :

மிக வலுவான மகிழுந்து மற்றும் பார உந்துகளின் சக்கரங்களின் திசையினை, குறைவான திருப்பு விசை கொண்டு எளிதில் மாற்ற திருப்புச்சக்கரம் உதவுகிறது.

திருப்புத்திறன்களின் தத்துவம் (Principle of moments):

சமநிலையில் உள்ள பொருள் ஒன்றின் மீது சம மதிப்புள்ள அல்லது சம மதிப்பற்ற விசைகள் இணையாகவோ அல்லது எதிர் இணையாகவோ செயல்பட்டால், அப்பொருளின் மீது செயல்படும் மொத்த வலஞ்சுழி திருப்புத்திறனும், மொத்த இடஞ்சுழி திருப்புத்திறனும் சமமாக இருக்கும்.

அல்லது சமநிலையில் உள்ள போது ஒரு புள்ளியின் மீது செயல்படும் அனைத்து விசைகளின் திருப்புத்திறன்களின் கூடுதல் சுழிக்கு சமமாகும்.

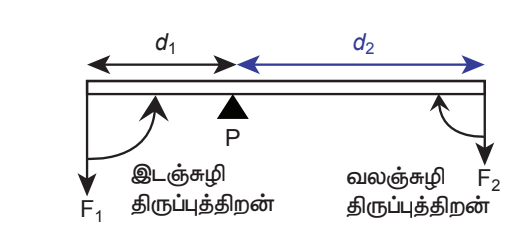
திருப்புத்திறன்களின் தத்துவம்.

சமநிலையில் உள்ள பொருள் ஒன்றில், ஆதார மையம் Pல் இருந்து d₁ தொலைவில் இயங்கும் விசையான F₁ இடப்பக்கச்சுழற்சியினையும், ஆதார மையம் Pல் இருந்து d₂ தொலைவில் இயங்கும் விசையான F₂ வலப்பக்கச் சுழற்சியினையும் ஏற்படுத்துகிறது.

திருப்புத்திறன்களின் தத்துவத்தின்படி

வலஞ்சுழி திருப்புத்திறன் = இடஞ்சுழி திருப்புத்திறன்

F₁ x d₁ = F₂ x d₂

நியூட்டனின் இரண்டாம் இயக்க விதி:

பொருள் ஒன்றின் மீது செயல்படும் விசையானது அப்பொருளின் உந்த மாறுபாட்டு வீதத்திற்கு நேர்தகவில் அமையும். மேலும் இந்த உந்த மாறுபாடு விசையின் திசையிலேயே அமையும். இவ்விதி விசையின் எண்மதிப்பை அளவிட உதவுகிறது. எனவே இதை “விசையின் விதி” என்றும் அழைக்கலாம்.

விசைக்கான சமன்பாட்டை கீழ்க் கண்டவாறு தருவிக்கலாம்.

m நிறை மதிப்புடைய பொருள் ஒன்று u என்ற ஆரம்ப திசைவேகத்தில் நேர்க்கோட்டு இயக்கத்தில் உள்ளதென கொள்வோம். t என்ற கால இடைவெளியில் F என்ற சமன் செயல்படாத புற விசையின் தாக்கத்தால், அதன் வேகம் v என்று மாற்றமடைகிறது.

பொருளின் ஆரம்ப உந்தம் P_i = mu

இறுதி உந்தம் P_t = mv

உந்தமாறுபாடு ∆p = P_t – P_i = mv – m u

நியூட்டனின் இரண்டாம் இயக்க விதிப்படி விசை F α உந்த மாற்றம் / காலம்

F α (mv – mu) / t

F = K m (v – u) / t

K என்பது விகித மாறிலி; K = 1 (அனைத்து அலகு முறைகளிலும்) எனவே

F = (mv – mu) / t

முடுக்கம் = திசை வேகமாற்றம் / காலம்;

A = (v – u) / t எனவே

F = m x a

விசை = நிறை x முடுக்கம்

சீரான திசைவேகத்தில் நகரும் பொருளினை, தொடர்ந்து நகர்ந்த புறவிசை ஏதும் தேவையில்லை. புறவிசைகளின் தொகுபயன் மதிப்பு சுழியாக இல்லை எனில் திசைவேக மதிப்பில் உறுதியாக மாற்றம் இருக்கும். உந்த மாற்றமானது விசையின் திசையிலேயே அமையும். இம்மாற்றமானது அதன் எண் மதிப்பிலோ, திசையிலோ அல்லது இவை இரண்டிலுமோ ஏற்படலாம்.

விசை முடுக்கத்தினை ஏற்படுத்துகிறது. சீரான வட்ட இயக்கத்தில் உள்ள பொருளின் திசைவேகத்தின் எண்மதிப்பு மாறிலியாகும். இருப்பினும் பொருளானது வட்டப்பாதையின் ஒவ்வோர் புள்ளியிலும் தனது திசையினை தொடர்ந்து மாற்றி கொள்வதால், திசைவேக மாறுபாடு ஏற்படுகிறது. இது முடுக்கத்தினை சுழற்சி ஆரத்தில் ஏற்படுத்துகிறது. இம்முடுக்கம் மைய விலக்கு முடுக்கம் எனப்படும். இம்முடுக்கம் உருவாக காரணமான விசை மைய விலக்கு விசை என்றழைக்கப்படுகிறது. இதைப்பற்றி ஒன்பதாம் வகுப்பில் நீங்கள் கற்றறிந்திருப்பீர்கள்.

விசையின் அலகு: விசையின் SI அலகு நியூட்டன் (N) ஆகும். அதன் CGS அலகு டைன் (Dyne) ஆகும்.

1 நியூட்டன் என்பதன் வரையறை: 1 கிலோகிராம் நிறையுடைய பொருளொன்றை 1 மீவி^-2 அளவிற்கு முடுக்குவிக்க தேவைப்படும் விசையின் அளவு 1 நியூட்டன் (1N) ஆகும். 1 நியூட்டன் = 1 கிகி மீவி^-2

1 டைன் என்பதன் வரையறை: 1 கிராம் நிறையுடைய பொருளொன்றை 1 செமீவி^-2 அளவிற்கு முடுக்குவிக்க தேவைப்படும் விசையின் அளவு 1 டைன் ஆகும். 1 டைன் = 1 கிசெமீவி^-2

1 நியூட்டன் = 10⁵ டைன்

ஓரலகு விசை:

1 கிலோகிராம் நிறையுள்ள பொருளொன்றை 1 மீவி^-2 அளவிற்கு முடுக்கவிக்க தேவைப்படும் விசையின் அளவு ஒரு நியூட்டன் (1N) ஆகும். இது ஓரலகு விசை என்றழைக்கப்படுகிறது.

ஈர்ப்பியல் அலகு விசை (Gravitational Unit of Force):

ஓரலகு நிறையுள்ள (1 கிகி) பொருளொன்றை புவியின் ஈர்ப்பு முடுக்கத்திற்கு (9.8 மீவி^-2) இணையாக முடுக்கவிக்க தேவைப்படும் விசையின் அளவு ஈர்ப்பியல் அலகுவிசை எனப்படும்.

ஈர்ப்பியல் அலகுவிசையின் SI அலகு, கிலோகிராம் விசை (kgf) ஆகும். CGS அலகு முறையில் கிராம் விசை (gf) ஆகும்.

1 kg f = f kg x 9.8 ms^-2 = 9.8 நியூட்டன்;

1 g f = 1 g x 980 cms^-2 = 980 டைன்

கணத்தாக்கு (Impulse):

மிகக்குறைந்த கால அளவில் மிக அதிக அளவு செயல்படும் விசை, கணத்தாக்கு விசை எனப்படும்.

F என்ற விசை t கால அளவில் ஒரு பொருள் மீது செயல்பட்டால், ஏற்படும் கணத்தாக்கு (J)ன் மதிப்பு, விசை மற்றும் கால அளவின் பெருக்கற் பலனுக்கு சமமாக இருக்கும்.

கணத்தாக்கு J = F x t

நியூட்டனின் இரண்டாவது இயக்க விதிப்படி

F = ∆p/t (∆p என்பது t கால இடைவெளியில் ஏற்படும் உந்தமாற்றம் என்பதை குறிக்கிறது)

∆p = F x t

சமன்பாடு 1.7 மற்றும் 1.8 ஐ சமன் செய்ய கணத்தாக்கு J = ∆p

கணத்தாக்கு என்பது உந்த மாறுபாட்டிற்கு சமமான அளவாகும். இதன் அலகு கிகி மீவி^-1 அல்லது நியூட்டன் விநாடி ஆகும்.

உந்த மாற்றம் அல்லது கணத்தாக்கு கீழ்க்கண்ட இரு வழிகளில் செயல்படலாம்.

1. பொருளின் மோதல் காலம் குறையும் போது அப்பொருளின் மீது செயல்படும் கணத்தாக்கு விசையின் மதிப்பு அதிகமாகும்.
2. பொருளின் மோதல் கால மதிப்பு அதிகமாகும் போது அப்பொருளின் மீது செயல்படும் கணத்தாக்க விசையின் மதிப்பு குறையும்.

சில எடுத்துக்காட்டுகள்:

• சீரற்ற பரப்பில் இருச்சக்கர வாகன பயணத்தின் போது கணத்தாக்கு விசை அதிர்வுகளை குறைப்பதற்கு சுருள்வில் அமைப்புகளும் அதிர்வுறிஞ்சிகளும் வைக்கப்பட்டுள்ளன.
• கிரிக்கெட் விளையாட்டில், வேகமாக வரும் பந்தினை பிடிக்க, விளையாட்டு வீரர் கையினை பின்னோக்கி இழுத்து மோதல் காலத்தை அதிகரிக்கிறார். இது அவரது கையில், பந்து ஏற்படுத்தும் கணத்தாக்கு விசையின் அளவை குறைக்கிறது.

`

கணத்தாக்கு விசைக்கு ஒரு எடுத்துக்காட்டு

நியூட்டனின் மூன்றாம் இயக்க விதி:

ஒவ்வொரு விசைக்கும் சமமான எதிர் விசை உண்டு. விசையும் எதிர்விசையும் எப்போதும் இரு வேறு பொருள்கள் மீது செயல்படும்.

A என்ற பொருள் ஒன்று B என்ற பொருளின் மீது F_A விசையினை செலுத்துகிறது எனில், “B” ஆனது தன் எதிர்விசை F_Bயினை “A” மீது செலுத்தும். இவற்றின் எண்மதிப்பு சமம். ஆனால் அவை ஒன்றுக்கொன்று எதிர்திசையில் செயல்படும்.

F_A = F_B

சில எடுத்துக்காட்டுகள்:

• பறவைகள் தமது சிறகுகளின் விசை(விசை) மூலம் காற்றினை கீழே தள்ளுகின்றன. காற்றானது அவ்விசைக்கு சமமான விசையினை (எதிர் விசை) உருவாக்கி பறவையை மேலே பறக்க வைக்கிறது.
• நீச்சல் வீரர் ஒருவர் நீரினை கையால் பின்நோக்கி தள்ளுதலின் மூலம் விசையினை ஏற்படுத்துகிறார். நீரானது அந்நபரை விசைக்கு சமமான எதிர்விசை கொண்டு முன்னே தள்ளுகிறது.
• துப்பாக்கி சுடுதலில் குண்டு, விசையுடன் முன்னோக்கி செல்ல அதற்கு சமமான எதிர்விசையினால் குண்டு வெடித்தபின் துப்பாக்கி பின்னோக்கி நகர்கிறது.

நேர்க்கோட்டு உந்த அழிவின்மை விதி:

புற விசை ஏதும் தாக்காத வரையில் ஒரு பொருள் அல்லது ஓர் அமைப்பின் மீது செயல்படும் மொத்த நேர்க்கோட்டு உந்தம் மாறாமல் இருக்கும்.

நேர்க்கோட்டு உந்த அழிவின்மை விதியினை கீழ் கண்ட ஒரு எடுத்துக்காட்டின் மூலம் நிரூபிக்கலாம்.

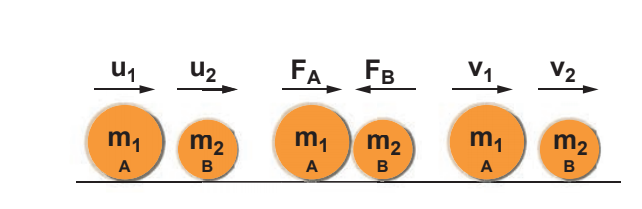
நேர்க்கோட்டு உந்த அழிவின்மை விதியினை நிரூபித்தல்

A மற்றும் B என்ற இருபொருட்களின் நிறைகள் முறையே m₁ மற்றும் m₂ என்க. அவை நேர்க்கோட்டில் பயணிப்பதாக கொள்வோம். u₁ மற்றும் U₂ என்பவை அவற்றின் ஆரம்ப திசை வேகங்களாக கொள்வோம். பொருள் Aனது Bஐ விட அதிக திசைவேகத்தில் செல்வதாக கருதுவோம் (U₁> U₂) “t” என்ற கால இடைவெளியில் பொருள் Aனது, B மீது மோதலை ஏற்படுத்துகிறது.

மோதலுக்குப் பிறகு அப்பொருள்கள் அதே நேர்க்கோட்டில் V₁ மற்றும் V₂ திசைவேகத்தில் பயணிப்பதாக கொள்வோம்.

நியூட்டனின் இரண்டாம் விதிப்படி

B யின் மீது A செயல்படுத்தும் விசை F_A = m₂ (V₂ – u₂)/t

அதேபோல் Aயின் மீது B செயல்படுத்தும் விசை F₈ = m₁ (V₁ – U₁)/t

நியூட்டனின் மூன்றாம் விதிப்படி Aன் மீது செயல்படும் விசையானது Bன் மீது செயல்படும் எதிர்விசைக்கு சமம்.

விசை எதிர்விசை

F₈ = -F_A

M1 (V – U)/t = – m (V – U)/t

M₁V₁ + M₂V₂ = m₁ u₁ + m₂ u₂

மேற்காண் சமன்பாடு, இந்நிகழ்வில் வெளிவிசையின் தாக்கம் எதும் இல்லாத போது, மோதலுக்கு பின் உள்ள மொத்த உந்த மதிப்பு, மோதலுக்கு முன் உள்ள மொத்த உந்த மதிப்பிற்கு சமம் என்பதை காட்டுகிறது. இது பொருளின் மீது செயல்படும் மொத்த உந்தம் ஒரு மாறிலி என்ற நேர்க்கோட்டு உந்த அழிவின்மை விதியினை நிரூபிக்கிறது.

ராக்கெட் ஏவுதல் நிகழ்வு:

ராக்கெட் ஏவுதலின் நியூட்டனின் மூன்றாம் விதி மற்றும் நேர்க்கோட்டு உந்த அழிவின்மை விதி, இவை இரண்டும் பயன்படுகின்றன. ராக்கெட்டுகளில் உந்து கலனில் (Propellant tank) எரிபொருள்கள் (திரவ அல்லது திட) நிரப்பப்படுகின்றன. அவை எரியூட்டப்பட்டதும், வெப்ப வாயுக்கள் ராக்கெட்டின் வால் பகுதியில் இருந்து அதிக திசைவேகத்தில் வெளியேறுகின்றன. அவை மிக அதிக உந்தத்தை உருவாக்குகின்றன. இந்த உந்தத்தை சமன் செய்ய, அதற்கு சமமான எதிர் உந்துவிசை எரிகூடத்தில் (Combustion Chamber) உருவாகி, ராக்கெட் மிகுந்த வேகத்துடன் முன்னோக்கி பாய்கிறது.

ராக்கெட் உயர பயணிக்கும் போது அதில் உள்ள எரிபொருள் முழுவதும் எரியும்வரை அதன் நிறை படிப்படியாக குறைகிறது. உந்த அழிவின்மை விதியின் படி நிறை குறைய குறைய, அதன் திசைவேகம் படிப்படியாக அதிகரிக்கிறது. ஒரு குறிப்பிட்ட உயரத்தில் ராக்கெட்டானது புவியின் ஈர்ப்பு விசையினை தவிர்த்து விட்டு செல்லும் வகையில், அதன் திசைவேக மதிப்பு உச்சத்தை அடைகிறது. இது விடுபடு வேம் (Escape Speed) எனப்படுகிறது.

ஈர்ப்பியல்:

நியூட்டனின் பொது ஈர்ப்பியல் விதி:

அண்டத்தில் உள்ள பொருட்களின் ஒவ்வோர் துகளும் பிற துகளை ஒரு குறிப்பிட்ட விசை மதிப்பில் ஈர்க்கிறது. அவ்விசையானது அவைகளின் நிறைகளின் பெருக்கற்பலனுக்கு நேர்விகிதத்திலும், அவைகளின் மையங்களுக்கிடையே உள்ள தொலைவின் இருமடிக்கு எதிர்விகிதத்திலும் இருக்கும். மேலும் இவ்விசை நிறைகளின் இணைப்புக் கோட்டின் வழியே செயல்படும்.

இவ்விசை எப்போதும் ஈர்ப்பு விசையாகும். இவ்விசை, நிறைகள் அமைந்துள்ள ஊடகத்தை சார்ந்தது அல்ல.

m₁ மற்றும் m₂ என்ற நிறையுடைய இரு பொருள்கள் r என்ற தொலைவில் வைக்கப்பட்டுள்ளதாக கருதுவோம். இவற்றிற்கிடையே உள்ள ஈர்ப்பு விசை F ஆனது, பொது ஈர்ப்பியல் விதிப்படி.

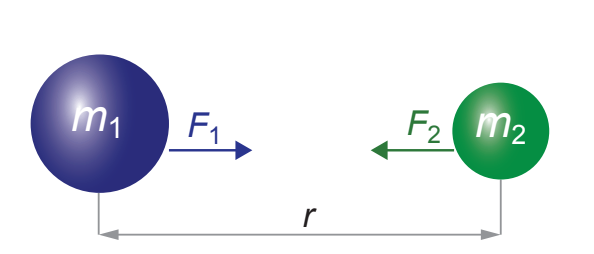
இரு நிறைகளுக்கு இடையே உள்ள ஈர்ப்பு விசை

F α m₁ x m₂

F α 1/r₂

இவை இரண்டையும் இணைத்து

F α m₁ x m₂ / r²

F = G m₁ m₂ / r²

G என்பது ஈர்ப்பியல் மாறிலி. இதன் மதிப்பு (SI அலகுகளில்) 6.674 x 10^-11 N m² kg^-2

புவிஈர்ப்பு முடுக்கம் (g):

பொருளொன்றை மேல்நோக்கி வீசினால் புவி ஈர்ப்பு விசையின் தாக்கத்தால், அதன் திசைவேகம் படிப்படியாக குறையும். ஒரு குறிப்பிட்ட உயரத்தில் அம்மதிப்பு முழுமையாக சுழி ஆகிறது. ஈர்ப்பு விசையினால் கீழே விழும் போது அதன் திசைவேகம் தொடர்ந்து மாற்றம் பெறுகிறது. இது அப்பொருளுக்கு முடுக்கத்தினை ஏற்படுத்தும். இம்முடுக்கம் புவி ஈர்ப்பு விசையினால் ஏற்படுவதால் புவிஈர்ப்பு முடுக்கம் என்றழைக்கப்படுகிறது.

புவி ஈர்ப்பு முடுக்கத்தின் சராசரி மதிப்பு (கடல் மட்டத்தில்) 9.8 மீ.வி^-2 ஆகும். இதன் பொருளானது, தடையின்றி கீழே விழும் பொருளின் திசைவேகம், ஒரு வினாடிக்கு 9.8 மீ வி^-1 என்ற அளவில் மாற்றம் பெறும் என்பதாகும். ‘g’ இன் மதிப்பு புவியில் அனைத்து இடங்களிலும் ஒரே மதிப்பாய் இருக்காது.

g மற்றும் G இவற்றிற்கிடையே உள்ள தொடர்பு:

m என்ற நிறையுள்ள பொருள் ஒன்று ஓய்வு நிலையில் புவி பரப்பின் மீது உள்ளது. பொருளின் மீது செயல்படும் இரு விசைகளை கீழ் கண்டவாறு கணக்கிடலாம். M என்பது புவியின் நிறையாக கொள்வோம். புவியின் நிறை புவி மையத்தில் குவிந்திருப்பதாக எடுத்துக்கொள்வோம். புவியின் ஆரம் R = 6378 கி.மீ (தோராயமாக = 6400 கி.மீ) ஆகும்.

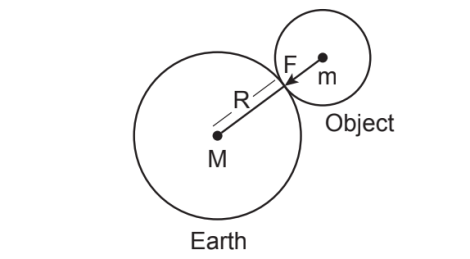
‘g’ மற்றும் ‘G’ இவற்றிற்கிடையே உள்ள தொடர்பு

நியூட்டனின் பொது ஈர்ப்பியல் விதிப்படி, புவிக்கும் பொருளுக்கும் உள்ள ஈர்ப்பு விசை

F = G M m / R² (1.11)

இதே போல் பொருள் மீது செயல்படும் விசை மதிப்பை நியூட்டனின் இரண்டாம் விதிப்படி கணக்கிடலாம். இவ்விதிப்படி விசையானது பொருளின் நிறைக்கும், முடுக்கத்திற்கும் உள்ள பெருக்கற்பலனாகும். இங்கு பொருளின் முடுக்கம், புவியின் ஈர்ப்பு முடுக்கத்திற்கு சமமாக இருப்பதால் ( a = g )

F = ma = mg (எடை) (1.12)

சமன்பாடுகள் (1.11) மற்றும் (1.12)னை சமன் செய்ய

இவற்றை சமன் செய்ய mg = GMm / R² (1.13)

எனவே புவி ஈர்ப்பு முடுக்கம் g = GM / R² (1.14)

இச்சமன்பாடு ‘g’ மற்றும் ‘G’ இவற்றிற்கிடையே உள்ள தொடர்பினை அளிக்கிறது.

புவியின் நிறை (M):

சமன்பாடு (1.14) ல் இருந்து புவியின் நிறை

M = g R² / G

G, R மற்றும் G ன் மதிப்புகளை பிரதியிட

புவியின் நிறை மதிப்பு M = 5.972 x 10²⁴ கிகி எனக் கணக்கிடப்படுகிறது.

புவி ஈர்ப்பு முடுக்க மாற்றம்:

புவிஈர்ப்பு முடுக்கம் g ன் மதிப்பு பூமியின் ஆரத்தை சார்ந்து அமையும். (g α 1/R²)புவியின் ஆரம் நிலநடுக்கோட்டுப் பகுதியில் அதிகமாக உள்ளதால், ஈர்ப்பு முடுக்கத்தின் மதிப்பு குறைவாக இருக்கும். துருவப் பகுதியில் ஆர மதிப்பு குறைவாக உள்ளதால், ஈர்ப்பு முடுக்கம் அதிகமாக இருக்கும்.

நாம் புவியின் தரைப்பகுதியில் இருந்து உயரச் செல்லச் செல்ல புவி ஈர்ப்பு முடுக்கம் படிப்படியாக குறையும். அதேபோல் புவியின் அடி ஆழத்திற்கு செல்லச் செல்ல புவிஈர்ப்பு முடுக்கத்தின் மதிப்பு குறைகிறது. புவியின் மையத்தில் ‘g’ ன் மதிப்பு சுழியாகும்.

நிறை மற்றும் எடை:

நிறை: நிறை என்பது பொருட்களின் அடிப்படை பண்பாகும். பொருட்களின் நிறை என்பது அதில் அடங்கியுள்ள பருப்பொருளின் அளவாகும். இதன் அலகு கிலோகிராம் ஆகும்.

எடை: ஒரு பொருளின் மீது செயல்படும் ஈர்ப்பு விசையின் மதிப்பு அப்பொருளின் எடை என்றழைக்கப்படுகிறது.

எடை W = நிறை (m) x புவி ஈர்ப்பு முடுக்கம் (g)

எடை ஓர் வெக்டார் அளவாகும். அது எப்போதும் புவியின் மையத்தை நோக்கி செயல்படும். அதன் அலகு நியூட்டன் (N). எடையானது புவிஈர்ப்பு முடுக்கத்தைச்

மின்தூக்கியின் நகர்விற்கேற்ப தோற்ற எடை மதிப்பு மாறுதல்

நிலை: 1 மின்தூக்கி a என்ற முடுக்க மதிப்பில் மேலே நகர்கிறது	நிலை: 2 மின்தூக்கி a என்ற முடுக்க மதிப்பில் கீழே நகர்கிறது	நிலை: 3 மின்தூக்கி ஓய்வில் உள்ளது (a=O) முடுக்கம் சுழியாகும்	நிலை : 4 மின்தூக்கி புவிஈர்ப்பு முடுக்க மதிப்பில் கீழே தடையின்றி விழுகிறது. (a=g)
R-W = F தொ = ma R = W + ma R = mg + ma R = m (g+a)	W – R = Fதொ = ma R = W – ma R = mg – ma R = m (g-a)	முடுக்கம் சுழியாகும் A = 0 W – R = Fதொ = O R = W R = mg	R = W – ma R = mg – ma A = g R = m (g-G) R = 0
R > W	R < W	R = W	R = 0
தோற்ற எடை, நிலையாக உள்ள போதுள்ள எடையை விட அதிகம்	தோற்ற எடை, நிலையாக உள்ள போதுள்ள எடையை விட குறைவு.	தோற்ற எடை, நிலையாக உள்ள போதுள்ள எடைக்கு சமம்.	தோற்ற எடையின் மதிப்பு சுழியாகும்.

சார்ந்தது. புவிஈர்ப்பு முடுக்கமதிப்பு புவியில் இடத்திற்கு இடம் மாறுபடுவதால், எடையின் மதிப்பும் இடத்திற்கு இடம் மாறுபடும். பொருட்களின் எடை துருவப்பகுதியில் அதிகமாகவும், நிலநடுக்கோட்டுப் பகுதியில் குறைவாக இருக்கும்.

நிலவில் ஈர்ப்பு முடுக்கத்தின் மதிப்பு 1.625 மீவி^-2 ஆகும். இது புவியின், ஈர்ப்பு முடுக்கத்தில் 0.1654 மடங்கிற்கு சமமான அளவாகும். 60 கிகி நிறையுள்ள ஒருவர் பூமியில் 588 N எடையுடன் (W = mg = 60 x 9.8 = 588 N) நிலவில் 97.5N (W= 60 x 1.625 = 97.5N) எடையுடன் இருப்பார். ஆனால் அவரது நிறை மதிப்பு (60 kg) புவியிலும் நிலவிலும் மாறாது இருக்கும்.

தோற்ற எடை (Apparent Weight):

ஓய்வு நிலையில் உள்ள போது உள்ள நமது உண்மை எடை (Actual Weight), மேலே அல்லது கீழே நாம் நகரும் போது அதே மதிப்பில் இருக்காது. புவிஈர்ப்பு விசை மட்டுமின்றி, இன்ன பிற விசைகளால் ஒரு பொருளின் எடையில் மாற்றம் ஏற்படும். இந்த எடை தோற்ற எடை என்றழைக்கப்படுகிறது.

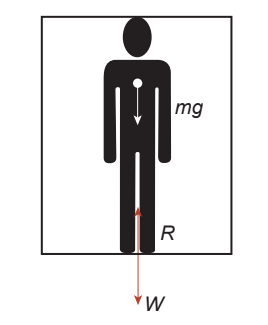
மின்தூக்கியில் ஒருவர் மேலும் கீழுமாக நகர்தல்

m நிறை கொண்ட ஒருவர் மின்தூக்கியில் மேலும் கீழுமாக நகர்வதாக கொள்வோம். ஓய்வு நிலையில் அவர் மீது செயல்படும் புவிஈர்ப்பு விசை, அவரது எடையாகும் (W). இது மின் தூக்கியின் தரைப்பரப்பின் கீழ் நோக்கி செங்குத்தாக செயல்படும். அவரது எடைக்கு சமமான எதிர்விசை மின் தூக்கியின் தரைப்பரப்பில் இருந்து செங்குத்தாக மேல்நோக்கி செயல்படுகிறது. இது தோற்ற எடை மதிப்பிற்கு (R) சமமாக எடுத்துக்கொள்ளப்படுகிறது.

மின்தூக்கியின் நகர்விற்கேற்ப, அவரது தோற்ற எடை மதிப்பு எவ்வாறு மாறுபடுகிறது என்பதை அறியலாம்.

எடை இழப்பு:

நீங்கள் கேளிக்கை பூங்கா சென்றபோது அங்கு சுழலும் பெரிய ராட்டினத்தில் விளையாடியதுண்டா? உருண்டோடும் தொடர் வண்டியில் (roller coaster) பயணித்ததுண்டா? இதில் மேலும் கீழும் பயணிக்கும் போது எவ்விதம் உணர்கிறீர்கள்?

மேலிருந்து கீழே ஒரு குறிப்பிட்ட முடுக்கத்தில் வரும் போது நமது எடை இழப்பது போன்ற தோற்றம் ஏற்படுகிறது அல்லவா? இது சில சமயங்களில் மின்தூக்கியில் நாம் நகரும் போதும் ஏற்படலாம்.

மேலிருந்து கீழே வரும் பொருளின் முடுக்கம், புவியின் ஈர்ப்பு முடுக்கத்திற்கு சமமாக உள்ள போது (a = g) “தடையில்லாமல் தானே விழும்

உருண்டோடும் தொடர் வண்டியில் எடை இழப்பு

நிலை”(free fall) ஏற்படுகிறது. இந்நிலையில் பொருளின் எடை முற்றிலும் குறைந்து சுழி நிலைக்கு வருகிறது. (R = m(g-g)=0) இது “எடையில்லா நிலை” (Weightlessness) என அழைக்கப்படுகிறது.

நாம், தோற்ற எடை இழப்பு மற்றும் தோற்ற எடை அதிகரிப்பை, வேகமாக சுழலும் பெரிய ராட்டினத்திலும், ஊஞ்சல் ஆட்டத்திலும், உருண்டோடும் தொடர் வண்டியிலும் உணரலாம்.

விண்வெளி வீரரின் எடையிழப்பு:

புவியினைச் சுற்றிவரும் விண்கலனில் வேலை செய்யும் விண்வெளிவீரர், அங்கு புவி ஈர்ப்பு விசை இல்லாததாலேயே மிதக்கிறார் என நாம் நினைக்கிறோம். இது தவறான கூற்றாகும்.

விண்வெளி வீரர் உண்மையில் மிதப்பதில்லை. விண்கலம் மிக அதிக சுற்றியக்க திசைவேகத்தில் நகர்ந்து கொண்டிருக்கிறது. அவர் அக்கலத்துடன் இணைந்து சம வேகத்தில் நகர்கிறார். அவரது முடுக்கம், விண்கல முடுக்கத்திற்கு சமமாக இருப்பதால், அவர் “தடையின்றி விழும் நிலை”யில் (free fall) உள்ளார். அப்போது அவரது தோற்ற எடை மதிப்பு சுழியாகும். (R = O) எனவே அவர் அக்கலத்துடன் எடையற்ற நிலையில் காணப்படுகிறார்.

நியூட்டனின் ஈர்ப்பியல் விதியின் பயன்பாடுகள்:

1. அண்டத்தில் உள்ள விண்பொருட்களின் பரிமாணங்களை அளவிட பொது ஈர்ப்பியல் வதி பயன்படுகிறது. புவியின் நிறை, ஆரம், புவி ஈர்ப்பு முடுக்கம் முதலியனவற்றை துல்லியமாக கணக்கிட இவ்விதி உதவுகிறது.
2. புதிய விண்மீன்கள் மற்றும் கோள்களை கண்டுபிடிக்க இவ்விதி உதவுகிறது.
3. சில நேரங்களில் விண்மீன்களின் சீரற்ற நகர்வு (Wobble) அருகில் உள்ள கோள்களின் இயக்கத்தை பாதிக்கும். அந்நேரங்கள் அவ்விண்மீன்களின் நிறையினை அளவிட இவ்விதி பயன்படுகிறது.

விண்வெளி வீரரின் எடையிழப்பு

1. தாவரங்களின் வேர் முளைத்தல் மற்றும் வளர்ச்சி புவியின் ஈர்ப்புவிசை சார்ந்து அமைவது “புவிதிசை சார்பியக்கம்” என்றழைக்கப்படுகிறது. இந்நிகழ்வை விளக்க இவ்விதி பயன்படுகிறது.
2. விண்பொருட்களின் பாதையினை வரையறை செய்வதற்கு இவ்விதி பயன்படுகிறது.

நினைவில் கொள்க:

• இயந்திரவியல்: விசையின் செயல்பாட்டால் பொருள் மீது ஏற்படும் விளைவுகளை பற்றி பயிலும் பாடம் இயந்திரவியல் ஆகும். இது இரண்டு பிரிவுகளாக பிரிக்கப்பட்டுள்ளது. அவை நிலையியல் மற்றும் இயங்கியல் ஆகும்.
• இயங்கியல் இரண்டு பிரிவுகளாக பிரிக்கப்பட்டுள்ளது. அவை இயக்கவியல் மற்றும் இயக்க விசையியல் ஆகும்.
• தன் மீது சமமற்ற புற விசை ஏதும் செயல்படாத வரை பொருளானது தமது ஓய்வு நிலையிலோ அல்லது சென்று கொண்டிருக்கும் நேர்க்கோட்டு இயக்க நிலையிலோ, தொடர்ந்து இருக்கும். இப்பண்பினை நிலைமம் என்றழைக்கிறோம். இது ஓய்வில் நிலைமம், இயக்கத்தில் நிலைமம், திசையில் நிலைமம் என மூன்று வகைகளாக பிரிக்கப்பட்டுள்ளது.
• நகரும் பொருளின் நிறை மற்றும் திசைவேகத்தின் பெருக்கற்பலனுக்கு சமமான அளவு உந்தம் எனப்படும். இது விசையின் திசையிலேயே செயல்படும்.
• ஒரு பொருள் மீது பல்வேறு விசைகள் செயல்படும்போது, அவைகளின் மொத்த விளைவை ஒரு தனித்த விசை மூலம் அளவிடலாம். இது “தொகுபயன் விசை” என்றழைக்கப்படுகிறது.
• இரட்டையின் திருப்புத் திறன் மதிப்பு ஏதெனும் ஒரு விசையின் எண்மதிப்பு மற்றும் இணை விசைகளுக்கு இடையே உள்ள செங்குத்து தொலைவு, இவைகளின் பெருகற்பலன் மதிப்பிற்கு சமமாகும்.
• திருப்புத்திறனின் திசை, பொருட்களின் வலஞ்சுழியாக இருப்பின் எதிர்குறியாகவும், இடஞ்சுழியாக இருப்பின் நேர்குறியாகவும் கொள்ளப்படுவது மரபாகும்.
• விசையின் அலகு SI முறையில் நியூட்டன் (N) மற்றும் CGS அலகு முறையில் டைன் (dyne) ஆகும்.
• கணத்தாக்கு மதிப்பானது (J) விசை (F) மற்றும் கால அளவின் (t) பெருக்கற் பலனுக்கு சமமாக இருக்கும்.
• புவிஈர்ப்பு முடுக்கம் g ன் மதிப்பு நிலநடுக்கோட்டுப் பகுதியில் குறைவாகவும் துருவப் பகுதியில் அதிகமாகவும் இருக்கும்.
• ஒரு பொருள் மீது செயல்படும் புவிஈர்ப்பு விசையின் மதிப்பு அப்பொருளின் எடை என்றழைக்கப்படுகிறது. இதன் அலகு நியூட்டன் அல்லது கிகி விசை (kg f)
• புவிஈர்ப்பு விசை மட்டுமின்றி, இன்ன பிற விசைகளால் ஒரு பொருளின் எடையில் மாற்றம் ஏற்படும். இந்த எடை தோற்ற எடை என்றழைக்கப்படுகிறது.
• மேலிருந்து கீழே வரும் பொருளின் முடுக்கம், புவியின் ஈர்ப்பு முடுக்கத்திற்கு சமமாக உள்ள போது எடை முற்றிலும் குறைந்து சுழி நிலைக்கு வருகிறது. இது “எடையில்லா நிலை” என அழைக்கப்படுகிறது.

மாதிரிக் கணக்குகள்:

1. 5 கிகி நிறையுள்ள பொருளொன்றின் நேர்க்கோட்டு உந்தம் 2.5 கிகி மீவி^-1 எனில் அதன் திசைவேகத்தை கணக்கிடுக.

தீர்வு:

தரவுகள்:

நிறை (m) = 5 கிகி

நேர்க்கோட்டு உந்தம் (p) = கிகி மீவி^-1

சூத்திரம்:

நேர்க்கோட்டு உந்தம் (p) = நிறை(m) x திசைவேகம்(v)

திசைவேகம் = நேர்க்கோட்டு உந்தம் / நிறை = 2.5/5

= 0.5 மீவி^-1

2. கீல் (keel) முனையில் இருந்து 90 செ.மீ தூரத்தில் கைப்பிடி கொண்ட கதவொன்று 40 N விசை கொண்டு திறக்கப்படுகிறது. கதவின் கீல் முனைப் பகுதியில் ஏற்படும் திருப்புத்திறன் மதிப்பினை கணக்கிடு.

தரவுகள்: விசையின் மதிப்பு F = 40 நியூட்டன்

விசை செயல்படும் தூரம் = கீல்முனை அமைந்துள்ள தொலைவு = d = 90 செ.மீ = 0.9 மீ

சூத்திரம்: திருப்புத்திறன் M = விசையின் மதிப்பு F x விசை செயல்படும் தொலைவு d

ஃ திருப்புத்தினை = 40 x 0.9 = 36 நியூட்டன் – மீட்டர்

3. புவியின் மேற்பரப்பின் மையத்தில் இருந்து எந்த உயரத்தில் புவியின் ஈர்ப்பு முடுக்கமானது, புவிமேற்பரப்பு ஈர்ப்பு முடுக்கத்தின் 1/4 மடங்காக அமையும்?

புவிமேற்பரப்பில் ஈர்ப்பு முடுக்கம் = g

புவிமையத்தில் இருந்து கணக்கீடு செய்ய வேண்டிய உயரம் R` = R + h

அவ்உயரத்தில் புவி ஈர்ப்பு முடுக்கம் g` = g/4

R` உயரத்தில் ஈர்ப்பு முடுக்கம் = g` = GMm/ (R`)²

புவிப்பரப்பில் ஈர்ப்பு முடுக்கம் = g = GMm/ (R)²

4 =

2 =

h = R

கணக்கீடு செய்ய வேண்டிய உயரம் R` = R + h

h = R ஆதலால்

R` = 2R

புவியின் மையத்தில் இருந்து, புவி ஆரத்தை போல் இருமடங்கு தொலைவில், ஈர்ப்பு முடுக்க மதிப்பு புவிப்பரப்பின் முடுக்கத்தைப்போல் 1/4 மடங்காக அமையும்.