அளவீடு Notes 9th Science Lesson 1 Notes in Tamil

அளவீடு Notes 9th Science Lesson 1 Notes in Tamil

அறிமுகம்

அறிவியல் சார்ந்த பிரிவுகள் அனைத்திற்கும் அளவீடுகளே அடிப்படை ஆகும். இது, நம்முடைய அன்றாட வாழ்க்கையிலும் முக்கியப்பங்கு வகிக்கிறது. உன் உயரத்தைக் காண்பது, உன் வீட்டிற்குப் பால் வாங்குவது, உனது நண்பன் ஓட்டப்பந்தயத்தில் ஓடிய நேரத்தைக் கணக்கிடுவது போன்ற செயல்களில் அளவீடுகள் தேவைப்படுகின்றன. அளவீடு என்பது எவ்வளவு நீளம், எவ்வளவு கனம், எவ்வளவு வேகம் போன்ற கேள்விகளுக்குப் பதிலளிக்கின்றது. அளவீடு என்பது, ஒரு பொருளின் பண்பையோ அல்லது நிகழ்வையோ மற்றொரு பொருளின் பண்பு அல்லது நிகழ்வுடன் ஒப்பிட்டு அப்பொருளுக்கு அல்லது நிகழ்வுக்கு ஒரு எண்மதிப்பை வழங்குவதாகும். ஒரு பொருளின் அளவு மற்றும் எண் மதிப்பைத் தீர்மானிப்பதே அளவீடு என்று வரையறுகப்படுகிறது. இந்தப் பாடப்பகுதியில் அளவீட்டின் அலகுகள் மற்றும் அளவிடும் கருவிகளின் பண்புகள் பற்றி நீங்கள் கற்றுக்கொள்ள இருக்கிறீர்கள்.

இயற்பியல் அளவுகள் மற்றும் அலகுகள்

இயற்பியல் அளவுகள்

• அளவிடக்கூடிய அளவுகளை இயற்பியல் அளவுகள் என்கிறோம். இயற்பியல் அளவுகளை இரண்டாக வகைப்படுத்தலாம். அவை: அடிப்படை அளவுகள் மற்றும் வழி அளவுகள் ஆகும்.
• வேறு எந்தவொரு அளவினாலும் அளவிட முடியாத அளவுகளை அடிப்படை அளவுகள் என்கிறோம். எடுத்துக்காட்டு: நீளம், நிறை, காலம் மற்றும் வெப்பநிலை. வேறு அளவுகளினால் அளவிடக்கூடிய அளவுகள் வழி அளவுகள் எனப்படும். எடுத்துக்காட்டு: பரப்பளவு, கன அளவு மற்றும் அடர்த்தி.
• இயற்பியல் அளவுகளுக்கு எண்மதிப்பும் (ஒரு எண்), அளவிடும் அலகும் உண்டு எடுத்துக்காட்டு: 3 கிலோகிராம். நீ கடை ஒன்றில் 3 கிலோகிராம் காய்கறிகள் வாங்குவதாக வைத்துக் கொள்வோம். இதில் 3 என்பது எண்மதிப்பு, கிலோகிராம் என்பது அலகு ஆகும். அலகுகளைப் பற்றி இப்பகுதியில் மேலும் காண்போம்.

அலகு

• அலகு என்பது தெரியாத அளவு ஒன்றுடன் ஒப்பிடக்கூடிய படித்தரமான அளவு ஆகும். விதி அல்லது மரபின்படி ஏற்றுக்கொள்ளப்பட்ட குறிப்பிட்ட எண்மதிப்பை உடைய இயற்பியல் அளவே அலகு என்று வரையறுக்கப்படுகிறது. உதாரணமாக, அடி என்பது நீளத்தை அளவிடக்கூடிய அலகு ஆகும். 10 அடி என்பது ‘1 அடி’ என்ற வரையறுக்கப்பட்ட நீளத்தை போன்று 10 மடங்கு என்பதைக் குறிக்கிறது.

முந்தைய காலங்களில், வெவ்வேறு அலகு மூறைகள் வெவ்வேறு நாட்டு மக்களால் பயன்படுத்தப்பட்டு வந்தன. அவ்வாறு பயன்படுத்தப்பட்ட அலகு முறைகள் அட்டவணையில் 1ல் தரப்பட்டுள்ளன.

அட்டவணை 1 பன்னாட்டு அலகு முறைகள்

அலகு முறை	நீளம்	நிறை	காலம்
CGS	சென்டிமீட்டர்	கிராம்	வினாடி
FPS	அடி	பவுண்ட்	வினாடி
MKS	மீட்டர்	கிலோகிராம்	வினாடி

ஆனால், இரண்டாம் உலகப்போரின் முடிவில், உலக அளவிலான அலகு முறைக்கான அவசியம் ஏற்பட்டது. எனவே, 1960 ஆம் ஆண்டு, பாரிஸ் நகரில், எடைகள் மற்றும் அலவுகளுக்கான பொது மாநாட்டில் SI அலகு முறையானது (பன்னாட்டு அலகுமுறை) உலக நாடுகளின் பயன்பாட்டிற்காக உருவாக்கப்பட்டு , பரிந்துரைக்கப்பட்டது.

SI அலகு முறை

• SI அலகு முறை என்பது பண்டைய அலகு முறைகளைவிட நவீனமயமான மற்றும் மேம்படுத்தப்பட்ட அலகு முறையாகும். ஏறக்குறைய உலகிலுள்ள அனைத்து நாடுகளாலும் இம்முறையானது ஏற்றுக்கொள்ளப்பட்டுள்ளது.
• இது, சில அடிப்படையான அலகுகளைக் கொண்டது. அந்த அடிப்படை அலகுகளிலிருந்து முறையான இணைப்பின் மூலம் பிற வழி அலகுகளைப் பெற முடியும். SI அலகு மூறையில் ஏழு அடிப்படை அலகுகள் (fundamental units) உள்ளன. அவை அடிமான அலகுகள் (base units) என்றும் வழங்கப்படுகின்றன. அவை அட்டவணையில் கொடுக்கப்பட்டுள்ளன.
• அடிப்படை அளவுகளை அளவிடப் பயன்படும் அலகுகள் அடிப்படை அலகுகள் என்றும் வழி அளவுகளை அளவிடப் பயன்படும் அலகுகள் வழி அலகுகள் என்றும் அழைக்கப்படுகின்றன.

அடிப்படை அளவுகளும் அவற்றின் அலகுகளும்

அடிப்படை அளவு	அலகு	குறியீடு
நீளம்	மீட்டர்	m
நிறை	கிலோகிராம்	kg
காலம்	வினாடி	s
வெப்பநிலை	கெல்வின்	K
மின்னோட்டம்	ஆம்பியர்	A
ஒளிச்செறிவு	கேண்டிலா	cd
பொருளின் அளவு	மோல்	mol

இந்த ஏழு அடிப்படை அலகுகளின் துணைகொண்டு, பிற வழி அளவுகளின் அலகுகள் வருவிக்கப்படுகின்றன. அவை அட்டவணையில் கொடுக்கப்பட்டுள்ளன.

அடிப்படை அலகுகள்

நீளம்

இரு புள்ளிகளுக்கு இடைப்பட்ட தொலைவு நீளம் என வரையறுக்கப்படுகிறது. நீளத்தின் SI அலகு மீட்டர் ஆகும். ஒளியானது 1/29,97,92,458 விநாடியில் வெற்றிடத்தில் கடக்கும் தூரமே ஒரு மீட்டர் எனப்படும்.

வழி அளவுகளும் அவற்றின் அலகுகளும்

வ.எண்	இயற்பியல் அளவு	வாய்ப்பாடு	அலகு
1	பரப்பு	நீளம் x அகலம்	மீ2 (m2)
2	பருமன்	நீளம் x அகலம் x உயரம்	மீ3 (m3)
3	அடர்த்தி	நிறை / பருமன்	கி கி/மீ3(kg/m3)
4	திசைவேகம்	இடப்பெயர்ச்சி / காலம்	மீ/வி (m/s)
5	உந்தம்	நிறை X திசைவேகம்	கி கிமீ/வி (kgms-1)
6	முடுக்கம்	திசைவேகம் / காலம்	மீ/வி2 (m/s2)
7	விசை	நிறை x முடுக்கம்	கி கிமீ/வி2 (kgms-2) அல்லது நியூட்டன் (N)
8	அழுத்தம்	விசை / பரப்பளவு	நியூட்டன்/மீ2 (N/m2) அல்லது பாஸ்கல் (Pa)
9	ஆற்றல் (வேலை)	விசை x தொலைவு	நியூட்டன் x மீ (Nm) அல்லது ஜுல் (J)
10	பரப்பு இழுவிசை	விசை / நீளம்	நியூட்டன் / மீ (N/m)

மிகப்பெரிய தூரங்களை (எ.கா: வானியல் பொருள்களுக்கிடையேயான தூரங்கள்) அளவிட நாம் கீழ்க்கண்ட அலகுகளைப் பயன்படுத்துகிறோம்.

• வானியல் அலகு
• ஒளி ஆண்டு
• விண்ணியல் ஆரம்

வானியல் அலகு (AU): வானியல் அலகு என்பது புவி மையத்திற்கும் சூரியனின் மையத்திற்கும் இடையேயான சராசரித் தொலைவு ஆகும்.

ஒரு வானியல் அலகு (1AU) = 1.496 x 10¹¹ மீ

ஒளி ஆண்டு: ஒளி ஆண்டு என்பது ஒளியானது வெற்றிடத்தில் ஓராண்டு காலம் பயணம் செய்யும் தொலைவு ஆகும்.

ஒரு ஒளி ஆண்டு = 9.46 x 10¹⁵மீ

விண்ணியல் ஆரம் (Parsec): விண்ணியல் ஆரம் என்பது சூரிய குடும்பத்திற்கு வெளியே உள்ள வானியல் பொருட்களின் தூரத்தை அளவிடப் பயன்படுகிறது.

ஒரு விண்ணியல் ஆரம் = 3.26 ஒளி ஆண்டு

பெரிய அலகுகள்

பெரிய அலகுகள்	மதிப்பு (மீட்டரில்)
கிலோமீட்டர் (km)	103மீ
வானியல் அலகு (AU)	1.496 x 1011மீ
ஒளி ஆண்டு	9.46 x 1015மீ
விண்ணியல் ஆரம்	3.08 x 1016மீ

• நமக்கு மிக அருகில் உள்ள நட்சத்திரம் ஆல்ஃபா சென்டாரொ (alpha centauri). சூரியனிலிருந்து 134 விண்ணியல் ஆரத்தொலைவில் இது உள்ளது. இரவு நேரங்களில் நமது வெறும் கண்ணிற்குத் தெரியும் நட்சத்திரங்கள் சூரியனிலிருந்து 500 விண்ணியல் ஆரத் தொலைவிற்குள் உள்ளன.

ஒரு மூலக்கூறில் உள்ள இரு அணுக்களுக்கு இடையேயான தொலைவு, உட்கருவின் அளவு, ஒளியின் அலைநீளம் போன்றவற்றை அளவிட பத்தின் துணைப் பன்மடங்குகள் பயன்படுகின்றன. இவை ஆங்ஸ்ட்ரம் என்ற அலகால் அளவிடப்படுகின்றன.

சிறிய அலகுகள்

சிறிய அலகுகள்	மதிப்பு (மீட்டரில்)
ஃபெர்மி (f)*	10-15மீ
ஆங்ஸ்ட்ரம் (A0)**	10-10மீ
நேனோமீட்டர் (nm)	10-9மீ
மைக்ரான் (மைக்ரோமீட்டர் m)	10-6மீ
மில்லி மீட்டர் (mm)	10-3மீ
சென்டி மீட்டர் (cm)	10-2மீ

SI அல்லாத பிற அலகு SI அலகுடன் பயன்படுத்துவது இல்லை

நிறை

• நிறை என்பது ஒரு பொருளில் உள்ள பருப்பொருட்களின் அளவாகும். நிறையின் SI அலகு கிலோகிராம். ஒரு கிலோகிராம் என்பது பிரான்ஸ் நாட்டில் செவ்ரஸ் எனும் இடத்திலுள்ள எடை மற்றும் அளவீடுகளுக்கான பன்னாட்டு அமைப்பில் வைக்கப்பட்டுள்ள பிளாட்டினம் – இரிடியம் உலோகக்கலவையால் செய்யப்பட்ட முன் மாதிரி உருளையின் நிறை ஆகும்.
• கிராம் மற்றும் மில்லிகிராம் ஆகிய அலகுகள், கிலோகிராம் என்ற அலகின் துணைப் பன்மடங்குகள் ஆகும். அதைப்போலவே, குவிண்டால் மற்றும் மெட்ரிக் டன் ஆகியவை கிலோகிராம் என்ற அலகின் பன்மடங்குகள் ஆகும்.

1 கிராம் = 1 / 1000 கி.கி. = 0.001 கிகி.

1 மில்லிகிராம் = 1 / 1000000 கி.கி. = 0.000001 கி.கி.

1 குவிண்டால் = 100 x 1கி.கி. = 100 கி.கி.

1 மெட்ரிக் டன் = 1000 க்ஷ் 1 கி.கி. = 10 குவிண்டால்

அணு நிறை அலகு

புரோட்டான், நியூட்ரான் மற்றும் எலக்ட்ரான் போன்ற துகள்களின் நிறையை அணுநிறை அலகால் அளவிடலாம்.

அணுநிறை அலகு (1 amu) = C¹² அணுவின் நிறையில் 1/12 மடங்கு ஆகும்.

• 1ml நீரின் நிறை = 1g
• 1l நீரின் நிறை = 1kg

(மற்ற திரவங்களின் நிறை அவற்றின் அடர்த்தியைப் பொறுத்து மாறுபடுகின்றன)

காலம்

• காலம் என்பது நிகழ்வுகளையும் அவற்றிற்கிடையேயான இடைவெளியையும் அளவிடக் கூடியதாகும். காலத்தின் SI அலகு வினாடி ஆகும். ஒளியானது 29,97,92,458 மீட்டர் தொலைவு வெற்றிடத்தில் பரவுவதற்குத் தேவையான காலம் ஒரு வினாடி ஆகும்.
• ஒரு வினாடி என்பது சராசரி சூரிய நாளின் 1/86,400 மடங்கு என்றும் வழங்கப்படுகின்றது. காலத்தின் மிகப் பெரிய அலகுகள் நாள், வருடம் மற்றும் மில்லினியம் ஆகும். 1 மில்லினியம் = 3.16 x 10⁹ வினாடி.

வெப்பநிலை

வெப்பநிலை

• வெப்பநிலை என்பது வெப்பம் மற்றும் குளிர்ச்சி ஆகியவற்றின் அளவைக் குறிக்கிறது. வெப்பநிலையின் SI அலகு கெல்வின் (K) ஆகும்.
• கெல்வின் என்பது வெப்ப இயக்கவியலின் வெப்பநிலையில் நீரின் முப்புள்ளியின் (Triple point of water) 1/ 273.16 பின்ன மதிப்பு ஆகும்.
• நீரின் முப்புள்ளி என்பது நிறைவுற்ற நீராவு, தூயநீர் மற்றும் உருகும் பனிக்கட்டி ஆகியவை சமநிலையில் இருக்கும் வெப்பநிலை ஆகும்.
• OK வெப்பநிலை என்பது பொதுவாக தனிச்சுழி வெப்பநிலை எனப்படும். வெப்பநிலையின் மற்ற அலகுகள் டிகிரி செல்சியஸ் (⁰C) மற்றும் ஃபாரன்ஹீட் (F) ஆகும்.

அலகுகளுக்கான முன்னீடுகள்

• அலகுகளுக்கான முன்னீடுகள் என்பவை, ஒரு அளவீட்டின் எண்ணளவைக் குறிப்பதாக ஒரு அலகின் குறியீட்டிற்கு முன்பாக எழுதப்படும் குறியீடுகள் ஆகும். அவை மிகப்பெரிய அல்லது மிகச்சிறிய அளவுகளைக் குறிப்பதற்கு பயன்படுகின்றன.
• கிலோமீட்டர் என்பதில் கிலோ (k) என்பது முன்னீடு ஆகும். முன்னீடு என்பது பத்தின் அடுக்கிலுள்ள நேர்க்குறி அல்லது எதிர்க்குறி எண்ணைக் குறிக்கின்றது. ஒரு சில அலகுகளுக்கான முன்னீடுகள் அட்டவணையில் கொடுக்கப்பட்டுள்ளன.
• இயற்பியல் அளவீடுகளின் மதிப்புகள் மிகப்பெரிய அளவில் மாறுபடக்கூடியவை. நாம் அணுவின் உட்கருவின் ஆரத்தினை 10^-15மீ எனவும், இரு விண்மீன்களுக்கு இடையேயான தொலைவை 10²⁶மீ எனவும் குறிக்கிறோம். எலக்ட்ரானின் நிறையை 9.11 x 10^-31 கி.கி எனவும், நமது பால்வழித்திரள் அண்டத்தின் நிறையை 2.2 x 10⁴¹kg எனவும் குறிக்கிறோம்.

அலகுகளுக்கான முன்னீடுகள்

பத்தின் மடங்கு	முன்னீடு	குறியீடு
1015	பீட்டா	P
1012	டெரா	T
109	ஜிகா	G
106	மெகா	M
103	கிலோ	k
102	ஹெக்டா	h
101	டெக்கா	da
10-1	டெசி	d
10-2	சென்டி	c
10-3	மில்லி	m
10-6	மைக்ரோ
10-9	நனோ	n
10-12	பிக்கோ	p
1015	ஃபெம்டோ	f

SI அலகுகளை எழுத பின்பற்ற வேண்டிய விதிகளும், மரபுகளும்

1. அறிவியல் அறிஞர்களின் பெயர்களால் குறிக்கப்படும் அலகுகளை எழுதும்போது, முதல் எழுத்து பெரிய எழுத்தாக (Capital Letter) இருக்கக் கூடாது. எ.கா. newton, henry, ampere, watt.
2. அறிவியல் அறிஞர்களின் பெயர்களால் குறிக்கப்படும் அலகுகளின் குறியீடுகளை எழுதும்போது பெரிய எழுத்தால் எழுத வேண்டும். எ.கா. newton என்பது N, henry என்பது H, ampere என்பது A, watt என்பது W.
3. குறிப்பிட்ட பெயரால் வழங்கப்படாத அலகுகளின் குறியீடுகளை சிறிய எழுத்தால் (Small Letter) எழுத வேண்டும். எ.கா. metre என்பது m மற்றும் kilogram என்பது kg.
4. அலகுகளின் குறியீடுகளுக்கு இறுதியிலோ அல்லது இடையிலோ நிறுத்தல் குறிகள் போன்ற எந்தக் குறியீடுகளும் பயன்படுத்தக் கூடாது. எ.கா: 50m என்பதை 50m. என்று குறிப்பிடக் கூடாது.
5. அலகுகளின் குறியீடுகளை பன்மையில் எழுதக் கூடாது. எ.கா. 10kg என்பதை 10kgs என எழுதக்கூடாது.
6. வெப்பநிலையை கெல்வின் (Kelvin) அலகால் குறிப்பிடும் போது டிகிரி குறி இடக் கூடாது. எ.கா: 283K என்பதை 283⁰K என எழுதக் கூடாது. (செல்சியஸ் மற்றும் பாரன்ஹீட் அலகுகளைக் குறிப்பிடும்போது டிகிரி குறி இட வேண்டும். எ.கா: 100⁰C மற்றும் 108⁰F என எழுத வேண்டுமே தவிர 100 C மற்றும் 108 F என எழுதக்கூடாது.)
7. அலகுகளின் குறியீடுகளை வகுக்கும்போது சரிவுக் (/) கோட்டினைப் பயன்படுத்தலாம். ஆனால் ஒன்றுக்கும் மேற்பட்ட சரிவுக் கோடுகளைப் பயன்படுத்தக் கூடாது. எ.கா: ms^-1 அல்லது m/s என எழுதலாம். J/ K/ mol என எழுதாமல் JK^-1mol^-1 என எழுத வேண்டும்.
8. எண் மதிப்பிற்கும், அலகுகளுக்கும் இடையில் இடைவெளி இடவேண்டும். எ.கா: 15 kgms^-1 என்று எழுத வேண்டுமே தவிர 15kgms^-1 என இடைவெளியின்றி எழுதக்கூடாது.
9. ஏற்றுக்கொள்ளப்பட்ட குறியீடுகளை மட்டுமே பயன்படுத்த வேண்டும். எ.கா: Ampere என்பதை amp என்றோ second என்பதை sec என்றோ எழுதக் கூடாது.
10. எந்தவொரு இயற்பியல் அளவின் எண் மதிப்பையும் அறிவியல் முறைப்படியே எழுத வேண்டும். எ.கா: பாதரசத்தின் அடர்த்தியை 13600 kgm^-3 என்று எழுதாமல் 1.36 x 10⁴ kgm^-3 என எழுத வேண்டும்.

வெர்னியர் அளவி

நமது அன்றாட வாழ்வில் பொருட்களின் நீளங்களை அளக்க நாம் மீட்டர் அளவுகோலைப் பயன்படுத்துகிறோம். அவை செமீ அளவிலும் மிமீ அள்விலும் குறிக்கப்பட்டிருக்கும். ஒரு மீட்டர் அளவுகோலினால் அளக்க முடிந்த மிகச் சிறிய அளவு அதன் மீச்சிற்றளவு எனப்படும். ஒரு மீட்டர் அளவியின் மீச்சிற்றளவானது 1 மிமீ ஆகும். இதனைப் பயன்படுத்தி பொருட்களின் நீளத்தினை மிமீ அளவுக்கு துல்லியமாக நாம் கணக்கிடலாம். வெர்னியர் அளவியைக் கொண்டு 0.1 மிமீ துல்லியமாகவும், திருகு அளவியைக் கொண்டு 0.01 மிமீ துல்லியமாகவும் நம்மால் அளவிட முடியும்.

வெர்னியர் அளவியின் அமைப்பு

• செமீ மற்றும் மிமீ அளவீடுகள் குறிக்கப்பட்ட ஒரு மெல்லிய உலோகப் பட்டையை வெர்னியர் அளவி கொண்டுள்ளது. இது முதன்மை அளவுகோல் எனப்படுகிறது.
• உலோகப் பட்டையின் இடப்பக்க முனையில் மேல்நோக்கிய மற்றும் கீழ் நோக்கிய தாடைகள் முதன்மைக் கோலுக்குச் செங்குத்தாகப் பொருத்தப்பட்டுள்ளன. இவை நிலையான தாடைகள் எனப்படும்.
• மேல் மற்றும் கீழ் நோக்கிய இயங்கும் தாடைகளை உடைய நழுவி நிலையான தாடையில் வலது புறத்தில் பொருத்தப்பட்டுள்ளது. திருகினைப் பயன்படுத்தி, நழுவியை நகர்த்தவும், நிலையாக ஓரிடத்தில் பொருத்தவும் முடியும்.
• வெர்னியர் அளவுகோலின் அளவீடுகள் நழுவியில் குறிக்கப்பட்டு, அது நழுவியுடனும் இயங்கும் தாடையுடனும் நகர்கிறது. கீழ்நோக்கிய தாடைகள் ஒரு பொருளின் வெளிப்புற அளவுகளை அளவிடவும், மேல்நோக்கிய தாடைகள் உட்புற அளவுகளை அளவிடவும் பயன்படுகின்றன. வெர்னியர் அளவுகோலின் வலது புறத்தில் இணைக்கப்பட்ட மெல்லிய பட்டை உள்ளீட்டற்ற பொருள்களின் ஆழத்தை அளவிடப் பயன்படுகிறது.

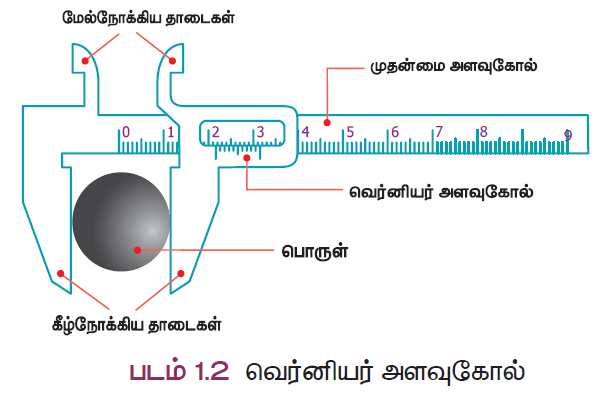
வெர்னியர் அளவியைப் பயன்படுத்துதல்

வெர்னியர் அளவியினைப் பயன்படுத்தும் போது மீச்சிற்றளவு, அளவிடும் எல்லை மற்றும் சுழிப்பிழையைக் கண்டறிவதே முதல்படி ஆகும்.

அ. மீச்சிற்றளவு

கருவியின் மீச்சிற்றளவு =

பெரும்பாலும் முதன்மைக்கோல் பிரிவு சென்டிமீட்டரிலும், அதன் உட்பிரிவுகள் மில்லி மீட்டரிலும் குறிக்கப்பட்டிருக்கும். எனவே, முதன்மைக்கோலின் மிகச்சிறிய அளவு ஒரு மில்லி மீட்டர் ஆகும். வெர்னியர் அளவுகோலில் மொத்தம் 10 பிரிவுகள் உள்ளன.

எனவே, மீச்சிற்றளவு = = 0.1 மிமீ = 0.01 செ.மீ

ஆ. சுழிப்பிழை

• திருகினை நெகிழ்த்தி நழுவியை இடப்பக்கம் நகர்த்தி, வெர்னியர் அளவியின் தாடைகள் ஒன்றோடு ஒன்று பொருந்துமாறு வைக்கவேண்டும். வெர்னியர் அளவுகோலின் சுழிப்பிரிவுடன் பொருந்தியுள்ளதா என்று சோதிக்கவும். அவை ஒன்றுடன் ஒன்று பொருந்தினால் சுழிப்பிழை இல்லையென்று பொருள்படும். அவ்வாறு பொருந்தவில்லையென்றால் அளவியில் சுழிப்பிழை உள்ளது என்று பொருள்படும்.
• சுழிப்பிழையானது நேர் சுழிப்பிழையாகவோ அல்லது எதிர் சுழிப்பிழையாகவோ இருக்கும். வெர்னியர் அளவுகோலின் சுழிப்பிரிவு முதன்மை அளவுகோலின் சுழிப்பிரிவிற்கு வலப்புறமாக அமைந்தால் அது நேர்சுழிப்பிழை எனப்படும். மாறாக, இடப்புறமாக அமைந்தால் அது எதிர்சுழிப்பிழை எனப்படும்.

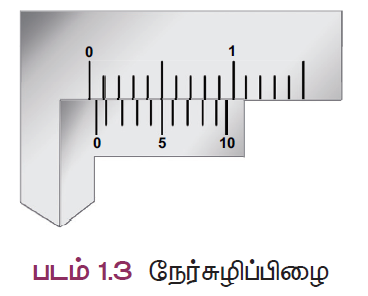
நேர் சுழிப்பிழை

• படம் நேர்சுழிப்பிழையைக் குறிக்கிறது. இப்படத்தில் வெர்னியர் அளவுகோலின் சுழிப்பிரிவு , முதன்மை அளவுகோலின் சுழிப்பிரிவிற்கு வலப்புறமாக நகர்ந்துள்ளது. அப்படியென்றால், நாம் அளக்கும் அளவானது உண்மையான அளவை விட அதிகமாக இருகும். எனவே இப்பிழையானது திருத்தப்படவேண்டும்.
• இப்பிழையைத் திருத்துவதற்கு, முதலாவதாக, வெர்னியர் அளவுகோலின் எந்தப்பிரிவு முதன்மை அளவுகோலின் ஏதாவது ஒரு பிரிவுடன் ஒன்றியிருக்கிறது எனப் பார்க்க வேண்டும்.
• இங்கு, ஐந்தாவது வெர்னியர் பிரிவு முதன்மைக் கோலின் பிரிவு ஒன்றுடன் ஒன்றியிருக்கிறது. எனவே, நேர்சுழிப்பிழை = +5 X LC = +5 x 0.01 = 0.05 செ.மீ.
• அப்படியெனில் சுழித்திருத்தம் எதிர்குறி ஆகும். எனவே, சுழித்திருத்தம் = – 0.05 செ.மீ.

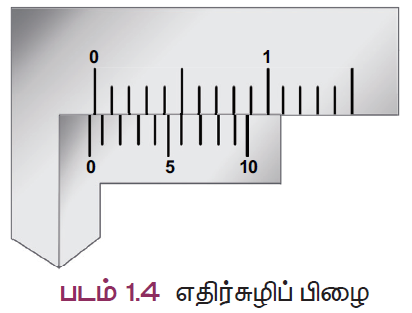
எதிர் சுழிப்பிழை

• இப்பொழுது படத்தைப் பார்க்கவும். வெர்னியர் அளவுகோலின் சுழிப்பிரிவு, முதன்மை அளவுகோலின் சுழிப்பிரிவிற்கு இடது புறமாக நகர்ந்துள்ளதை நாம் காணலாம். எனவே, நாம் பெறும் அளவானது உண்மையான அளவை விட கூறைவாக இருக்கும். இப்பிழையை சரி செய்ய வேண்டுமெனில், நாம் ஏர்கனவே செய்தது போல வெர்னியர் அளவுகோலின் எந்தப் பிரிவு, முதன்மை அளவுகோலின் ஏதாவது ஒரு பொரிவுடன் ஒன்றியுள்ளது என்பதைக் காண வேண்டும்.
• இப்பாடத்தில், ஆறாவது பிரிவு ஒன்றியிருக்கிறது. ஆனால் எதிர்சுழிப்பிழையைக் கணக்கிடும்போது பின்புறத்திலிருந்து கணக்கிட வேண்டும் (10 வது பிரிவிலிருந்து). அப்படியெனில், நான்காவது கோடு ஒன்றியிருக்கிறது. எனவே, எதிர்சுழிப்பிழை = -4 x LC = -4 x 0.01 = 0.04 செ.மீ.

அப்படியெனில் சுழித்திருத்தம் நேர்குறி ஆகும். எனவே, சுழித்திருத்தம் = +0.04 செ.மீ.

பொதுவாக, வெர்னியர் அளவியைப் பயன்படுத்தி பல்வேறு பொருள்களின் பரிமாணங்களைக் கணக்கிடலாம். பொருள்களின் நீளம், அகலம், உயரம் ஆகியவற்றைக் கணக்கிட்டுவிட்டால் அவற்றின் கனஅளவைக் கணக்கிடலாம். எடுத்துக்காட்டாக, ஒரு முகவையின் உள்விட்டத்தையும் (சரியான தாடைகளைப் பயன்படுத்தி) அதனுடைய ஆழத்தையும் (ஆழம் கணிப்பானைப் பயன்படுத்தி) கணக்கிட்டு, அதன் மூலம் முகவையின் உட்புற கன அளவையும் கணக்கிடலாம்.

எண்ணிலக்க (Digital) வெர்னியர் அளவி

இன்று நாம் எண்ணிலக்க உலகில் (Digital world) வாழ்ந்து கொண்டிருக்கிறோம். எனவே, வெர்னியர் அளவியும் எண்ணிலக்க வெர்னியர் அளவி என்ற புதிய பரிணாமத்தைப் பெற்றுள்ளது.

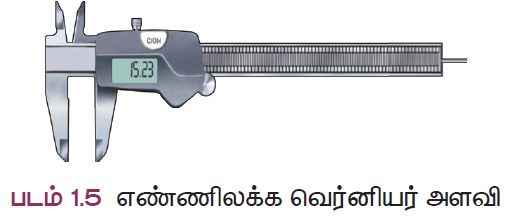
எண்ணிலக்க வெர்னியர் அளவியின் நழுவியின் மீது ஒரு எண்காட்டி அமைப்பும் மின்னணு கணகீட்டுக் கருவியும் அமைக்கப்பட்டுள்ளன. இது அளவீட்டினைக் கணக்கிட்டு எண்காட்டி மூலம் காட்சிப்படுத்தும். இதனால் பயன்படுத்தப்படும் கருவியின் மீச்சிற்றளவு, சுழிப்பிழைத் திருத்தம் போன்றவற்றைக் கணக்கிட வேண்டிய தேவை இல்லை.

திருகு அளவி

திருகு அளவி ஒரு மில்லி மீட்டரில் நூறில் ஒரு பங்கு (0.01 மிமீ) அளவிற்குத் துல்லியமாக அளவிடும் கருவியாகும். இக்கருவியைக் கொண்டு மெல்லிய கம்பியின் விட்டம், மெல்லிய உலோகத் தகட்டின் தடிமன் போன்றவற்றை அளவிட முடியும்.

திருகு அளவியின் அமைப்பு

திருகு அளவியில் ‘U’ வடிவ உலோகச் சட்டம் உள்ளது. இச்சட்டத்தின் ஒரு புறம் உள்ளீடற்ற ஒரு உலோக உருளை பொருத்தப்பட்டுள்ளது. உருளையின் உட்புறம் புரிகள் செதுக்கப்பட்டிருக்கும். புரியினுள் திருகு ஒன்று இயங்குகிறது (படம்). உருளையின் மேல்புறத்தில் திருகின் அச்சுக்கு இணையாக மில்லி மீட்டர் அளவுகள் குறிக்கப்பட்ட அளவுகோல் உள்ளது. இது புரிக்கோல் (PS) எனப்படும். திருகின் தலைப்பகுதியோடு உள்ளீடற்ற உருளையொன்று இணைக்கப்பட்டுள்ளது. அதன் குவிந்த முனை 100 பிரிவுகளைக் கொண்டது. இது தலைக்கோல் (HS) எனப்படும். ‘U’ வடிவ சட்டத்தின் ஒரு முனையில் நிலையான முனை ஒன்றும் அதற்கெதிரே நகரக்கூடிய முனை ஒன்றும் உள்ளன. திருகின் தலைப்பகுதியில் உள்ள பற்சட்ட அமைப்பு (பாதுகாப்பு அமைப்பு) திருகானது அளவுக்கு அதிகமாகத் திருகப்படுவதைத் தடுக்கும் வகையில் அமைந்துள்ளது.

திருகு அளவியைப் பயன்படுத்துதல்

நிலையான உலோக உருளைக்கு மேல் உள்ள திருகைச் சுற்றும் பொழுது, அதன் முனை முன்னோக்கி நகரும் தொலைவு, சுற்றப்பட்ட சுற்றுக்களின் எண்ணிக்கை நேர் தகவில் அமையும் என்ற திருகுத் தத்துவத்தின் அடிப்படையில் திருகு அளவி இயங்கிறது.

அ. புரியிடைத் தூரம்

ஒரு முழுச் சுற்றுக்கு திருகின் முனை நகரும் தொலைவு புரியிடைத் தூரம் எனப்படும். திருகு அளவியில் இதன் அளவு 1 மிமீ ஆக உள்ளது.

புரியிடைத் தூரம் =

ஆ. திருகு அளவியின் மீச்சிற்றளவு

திருகின் தலைப்பகுதி, தலைக்கோலின் ஒரு பிரிவு அளவிற்குச் சுற்றும்பொழுது திருகின் முனை நகரும் தூரம், திருகு அளவியின் மீச்சிற்றளவு ஆகும்.

மீச்சீற்றளவு (LC) =

= 1 மிமீ / 100= 0.01 மி.மீ

இ. திருகு அளவியின் சுழிப்பிழை

நகரும் முனையின் சமதளப் பரப்பும் எதிரேயுள்ள நிலையான முனையின் சமதளப்பரப்பும் இணையும்பொழுது, தலைக்கோலின் சுழிப்பிரிவு, புரிக்கோலின் வரைகோட்டுடன் இணைந்தால் சுழிப்பிழை ஏதும் இல்லை.

நேர் சுழிப்பிழை

திருகு முனையின் சமதளப் பரப்பும், எதிரேயுள்ள குமிழின் சமதளப்பரப்பும் இணையும்போது தலைக்கோலின் சுழிப்பிரிவு புரிக்கோலின் வரைகோட்டிற்குக் கீழ் அமைந்தால் அது நேர் சுழிப்பிழை எனப்படும். எடுத்துக்காட்டாக தலைக்கோலின் 5வது பிரிவு புரிக்கோலின் வரைகோட்டுடன் இணைந்துள்ளது (படம்). எனவே, இது நேர் சுழிப்பிழை எனப்படும்.

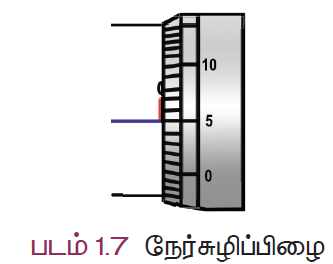
நேர்சுழிப்பிழை = +(n x LC),

n என்பது தலைக்கோல் ஒன்றிப்பு, இங்கு n = 5.

எனவே, நேர்சுழிப்பிழை = +(5 x 0.01) = 0.05 மி.மீ

சுழித்திருத்தம் = -0.05மி.மீ

எதிர் சுழிப்பிழை

• திருகுமுனையின் சமதளப்பரப்பும் எதிர்முனையின் சமதளப்பரப்பும் இணையும் போது, தலைக்கோலின் சுழிப்பிரிவு புரிகோலின் வரைகோட்டுக்கு மேல் அமைந்தால் அது எதிர்சுழிப் பிழை எனப்படும்.
• எடுத்துக்காட்டாக , இப்படத்தில் தலைக்கோலின் 95-வது பிரிவு புரிக்கோலின் வரை கோட்டுடன் இணைந்துள்ளது (படம்). இது எதிர்சுழிப் பிழையாகும்.

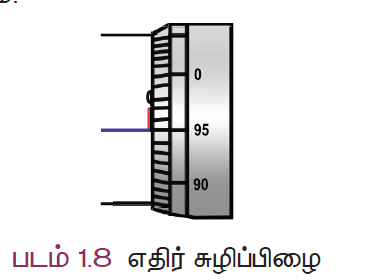
எதிர்பிழை = -(100 –n) x LC

எதிர்பிழை = -(100 -95) x LC

= -5 x 0.01

= -0.05 மி.மீ

சுழித்திருத்தம் (Z.C) = +0.05 மி.மீ

நிறையை அளவிடுதல்

• அன்றாட வாழ்வில் நாம் நிறை என்ற வார்த்தைக்குப் பதிலாக எடை என்ற வார்த்தையையே பயன்படுத்துகிறோம். வணிக முறையிலும் பொருட்களை நிறை என்ற அடிப்படையில்தான் அளவிடுகிறார்கள்.
• நிறையின் SI அலகு கிலோகிராம் ஆகும். ஆனால் நாம் வாங்கும் பொருட்களைப் பொறுத்து அவற்றை பல்வேறு நிறை அலகுகளில் வாங்குகிறோம். எடுத்துக்காட்டாக நாம் தங்கம் வாங்கும்போது கிராம் மற்றும் மில்லி கிராம் அளவுகளிலும், மருந்துகள் வாங்கும்போது மில்லி கிராம் அளவுகளிலும், மளிகைக் கடையில் பொருட்கள் வாங்கும் பொழுது கிராம் மற்றும் கிலோகிராம் அளவுகளிலும் வாங்குகிறோம். ஏற்றுமதிப் பொருட்களை டன்கள் அடிப்படையில் அளவிடுகிறோம்.
• ஒரே கருவியைப் பயன்படுத்தி மேற்கண்ட பொருட்களை அளவீடு செய்ய முடியுமா? சிறிய அளவு நிறைகளையும், பெரிய அளவு நிறைகளையும் அளவிட தனித்தனியான கருவிகளைத் தான் பயன்படுத்த முடியும். இந்தப் பகுதியில் சிறிய மற்றும் பெரிய நிறையை அளவீடு செய்யத் தேவையான கருவிகளைப் பற்றித் தெரிந்து கொள்வோம்.
• ஒரு முட்டையின் ஓடானது அந்த முட்டையின் எடையில் 12% ஆகும். ஒரு நீலத் திமிங்கலத்தின் எடை 30 யானைகளின் எடைக்குச் சமம். அதன் நீளம் மூன்று பேருந்துகளின் நீளத்திற்குச் சமம்.

பொதுத்தராசு

படித்தர நிறைகளோடு (Standard mass) பொருட்களை ஒப்பிட்டு அளவீடு செய்யப்பயன்படும் கருவி பொதுத்தராசு ஆகும். (படித்தர நிறைகள் : 5கி, 10கி, 20கி, 50கி,1 00கி, 200கி, 500கி, 1கி.கி, 2 கி.கி, 5கி.கி) சாதாரணத் தராசினைக் கொண்டு 5 கி என்ற அளவுவரை துல்லியமாக அளவிட முடியும் (படம்).

இயற்பியல் தராசு

இயற்பியல் தராசு ஆய்வகங்களில் பயன்படுத்தப்படுகிறது. இது சாதாரணத் தராசினைப் போன்றதாகும். ஆனால் இத்தராசு அதிகத் துல்லியத்தன்மையைப் பெற்றுள்ளது. இயற்பியல் தராசினைப் பயன்படுத்தி மில்லி கிராம் அளவில் துல்லியமாக அளவிட முடியும் (படம்).

இயற்பியல் தராசில் பயன்படுத்தப்படும் படித்தர நிறைகள் முறையே 10 மிகி, 20 மிகி, 50 மிகி, 100 மிகி, 200 மிகி, 500 மிகி, 1 கி, 2 கி, 5 கி, 10 கி, 20 கி, 50 கி, 100 கி மற்றும் 200 கி ஆகும்.

எண்ணியல் தராசு

தற்காலத்தில் பொருளின் நிறையைக் கணக்கிட மிகத் துல்லியத் தன்மையுடன் கூடிய எண்ணியல் தராசைப் பயன்படுத்துகின்றனர். பொருளின் நிறையை மில்லிகிராம் அளவிற்கு மிகத் துல்லியமாக அளவிடுகிறார்கள். இக்கருவியின் மீச்சிற்றளவு 10 மி.கி. அளவிற்கு இருக்கிறது (படம்). இத்தகைய தராசுகளைக் கையாள்வது எளிது. இவை, ஆய்வகங்கள் மற்றும் நகைக் கடைகளில் பயன்படுத்தப்படுகின்றன.

சுருள் வில் தராசு

• சுருள் வில் தராசு பொருளின் எடையைக் கணக்கிடப் பயன்படுகிறது. இக்கருவி உலோக உள்ளீடற்ற சட்டத்தினுள் எஃகு சுருள்வில்லைப் பொருத்தி அமைக்கப்பட்ட அமைப்பாகும். இதன் மேல் முனை நிலையான வளையத்தோடு பொருத்தப்பட்டிருக்கும். அதன் கீழ் முனையானது பொருளோடு பொருந்தக் கூடிய வளையத்தோடு இணைக்கப்பட்டிருக்கும். இது “சுருள்வில்லில் கொடுக்கப்படும் விசையானது நிலையான புள்ளியிலிருந்து சுருள்வில் விரிவடையும் தொலைவிற்கு நேர் தகவில் அமையும்” என்ற ஹூக்ஸ் விதிப்படி இயங்குகிறது (படம்).
• குறிமுள் ஒன்று அளவுகோல் மீது நகர்ந்து செல்லும் சட்டத்தின் மீது வலது புறத்தில் இணைக்கப்பட்டுள்ளது. பொருளின் எடைக்கேற்ப சுருள்வில் விரிவடையும்போது தராசின் வலப்பக்கம் உள்ள அளவுகோலில் அளவீட்டை குறிமுள் காட்டும். இதுவே அப்பொருளின் எடையாகும்.

நிறை – எடை வேறுபாடு

• நிறை (m) என்பது ஒரு பொருளில் உள்ள பருப்பொருள்களின் அளவாகும். எடை (w) என்பது ஒரு பொருளின் மீது செயல்படும் புவியீர்ப்பு விசையை சமன்செய்வதற்காக அந்தப் பொருளின் பரப்பினால் செலுத்தப்படும் எதிர் விசை ஆகும்.
• உதாரணமாக, ஒரு சுருள்வில் தராசின் சுருளில் ஏற்படும் இழுவிசை, பொருளின் மீது செயல்படும் புவியீர்ப்பு விசையைச் சமன்செய்கிறது. ஒரு மனிதனின் தரையின் மீது நிற்கும்போது, தரையானது புவியீர்ப்பு விசைக்குச் சமமான எதிர்விசையை அந்த மனிதனின் மீது செலுத்துகிறது. எந்தவொரு பொருளின் மீதும் செயல்படும் புவியீர்ப்பு விசை mg என்று வழங்கப்படுகீறது. இதில் m என்பது ஒரு பொருளின் நிறை ; g என்பது புவியீர்ப்பு முடுக்கம் ஆகும்.
• நிலவில் ஈர்ப்பு விசையானர்து புவியீர்ப்பு விசையில் 1/6 மடங்காக இருக்கும். எனவே, நிலவில் ஒரு பொருளின் எடை புவியில் உள்ள எடையை விட குறைவாக இருக்கும். நிலவில் புவியீர்ப்பு முடுக்கம் 1.63 மீ/வி² ஆகும்.
• 70 கி.கி நிறையுள்ள மனிதனின் எடை புவியில் 686 நியூட்டனாகவும், நிலவில் 114 நியூட்டனாகவும் உள்ளது. ஆனால் நிலவில் அவரது நிறை 70 கிலோகிராமாகவே உள்ளது.

நிறை – எடை வேறுபாடு

நிறை	எடை
அடிப்படை அளவு	வழி அளவு
எண் மதிப்பு மட்டும் கொண்ட அளவு. எனவே, இது ஸ்கேலர் அளவாகும்.	எண் மதிப்பு மற்றும் திசைப் பண்பு கொண்டது, எனவே, இது வெக்டர் அளவாகும்.
பொருளில் உள்ள பருப்பொருட்களின் அளவாகும்.	பருப்பொருட்களின் மீது செயல்படும் புவியீர்ப்பு விசையின் அளவாகும்.
இடத்திற்கு இடம் மாறாது.	இடத்திற்கு இடம் மாறுபடும்.
இயற்பிடல் தராசினால் அளவீடு செய்யப்படுகிறது.	சுருள்வில் தராசு கொண்டு அளவீடு செய்யப்படுகிறது.
இதன் அலகு கிலோகிராம்.	இதன் அலகு நியூட்டன்.

அளவீடுகளில் துல்லியம்

இயற்பியல் அளவுகளை அளவிடும்போது, துல்லியம் என்பது அவசியமாகும். துல்லியம் என்பது நாம் அளக்கும் அளவீடானது எந்த அளவிற்கு உண்மையான அளவீட்டோடு ஒன்றி வருகிறது என்பதைக் குறிக்கிறது. அளவீடுகளில் துல்லியம் என்பது பொறியியல், இயற்பியல் மற்றும் அனைத்து அறிவியல் பிரிவுகளுக்கும் மையமாக இருக்கிறது. துல்லியம் என்பது நம் அன்றாட வாழ்க்கையிலும் அவசியமானதாகும். நகைக் கடைகளில் எவ்வளவு துல்லியமாக தங்கத்தை அளவிடுகிறார்கள் என்பதை நீங்கள் பார்த்திருப்பீர்கள். உணவு சமைக்கும்போது, உப்பின் அளவு சிறிது அதிகமாகி விட்டால் என்ன ஆகும்? எனவே, அளவீடுகளை மேற்கொள்ளும்போது, துல்லியமாக அளவிடுவது அவசியமாகும்.

பிழையான அளவிடும் கருவிகள் மற்றும் அளவிடுபவர் புரியும் பிழைகளால் துல்லியமற்ற மதிப்புகள் கிடைக்கின்றன. துல்லியமான அளவுகளைப் பெறுவதற்கு, அளவிடும் கருவியின் துல்லியத்தன்மையை சரிபார்ப்பது என்பது எப்பொழுதும் முக்கியமானதாகும். மேலும், அளவீடுகளை மீண்டும் மீண்டும் செய்து சராசரியைக் காண்பதன் மூலமும் பிழைகளைச் சரிசெய்து அளவிடும் அளவுகளின் துல்லியமான மதிப்பினைப் பெறமுடியும்.