Motion Notes 9th Science Lesson 2 Notes in English

Motion Notes 9th Science Lesson 2 Notes in English

Introduction

• Motion is the change in the position of an object with respect to its surrounding.
• Everything in the universe is in motion.
• Even though an object seems to be not moving, actually it is moving because the Earth is moving around the Sun.
• You may see objects moving in your surroundings.
• Cars along the road, trains along the track and aeroplanes in the sky are all moving.
• These movements are one type of motion. You may see the fan rotating in the ceiling.
• This is another type of motion. When you are playing in swing, it moves to and fro. This is also a type of motion.
• Motion is described in terms of distance, speed, acceleration and time.
• In this lesson we will study about different types and equations of motion, displacement, velocity and acceleration.

Rest and Motion

Activity

• Look around you. You can see many things: a row of houses, large trees, small plants, flying birds, running cars and many more.
• List the objects which remain fixed at their position and the objects which keep on changing their position.
• In physics, the objects which do not change their position are said to be at rest, while those which change their position are said to be in motion.
• For example, a book lying on a table and the walls of a room are at rest.
• Cars and buses running on the road, birds and aeroplanes flying in air are in motion.
• Motion is a relative phenomenon. This means that an object appearing to be in motion to one person can appear to be at rest as viewed by another person.
• For example, trees on road side would appear to move backward for a person travelling in a car while the same tree would appear to be at rest for a person standing on the road side.

Types of Motion

• In physics, motion can be classified as below.
• Linear motion: Motion along a straight line.
• Circular motion: Motion along a circular path.
• Oscillatory motion: Repetitive to and fro motion of an object at regular interval of time.
• Random motion: Motion of the object which does not fall in any of the above categories.

Uniform and Non-uniform motion

Uniform motion

• Consider a car which covers 60 km in the first hour, 60 km in the second hour, and another 60 km in the third hour and so on.
• The car covers equal distance at equal interval of time.
• We can say that the motion of the car is uniform.
• An object is said to be in uniform motion if it covers equal distances in equal intervals of time howsoever big or small these time intervals may be.

Non-uniform motion

• Now, consider a bus starting from one stop.
• It proceeds slowly when it passes through crowded area of the road.
• Suppose, it manages to travel merely 100 m in 5 minutes due to heavy traffic and is able to travel about 2 km in 5 minutes when the road is clear.
• Hence, the motion of the bus is non-uniform i.e. it travels unequal distances in equal intervals of time.
• Thus, an object is said to be in non- uniform motion if it covers unequal distances in equal intervals of time.

Distance and Displacement

• Consider a body moving from the point A.
• It moves along the path given in the Figure and reaches the point B.
• The total length of the path travelled by the body from A to B is called distance travelled by the body.
• The length of the straight line AB is called displacement of the body.

Distance

• The actual length of the path travelled by a moving body irrespective of the direction is called the distance travelled by the body.
• It is measured in metre in SI system.
• It is a scalar quantity having magnitude only.

Displacement

• It is defined as the change in position of a moving body in a particular direction.
• It is a vector quantity having both magnitude and direction.
• It is also measured in metre in SI system.

Speed, Velocity and Acceleration

• Speed is the quantity which shows how fast the body is moving but velocity is the quantity which shows the speed as well as the direction of the moving body.

Speed

• Speed is the rate of change of distance or the distance travelled in unit time.
• It is a scalar quantity.
• The SI unit of speed is ms–1.
• Speed = Distance travelled / Time taken

Problem 1

• An object travels 16 m in 4 s and then another 16 m in 2 s.
• What is the average speed of the object?

Solution:

• Total distance travelled by the object = 16 m + 16 m = 32 m
• Total time taken = 4s + 2s = 6s
• Average speed = Total distance travelled / Total time taken ­
• 32 / 6 m s = 5.33 ms–1
• Therefore, the average speed of the object is 5.33 ms–1

Problem 2

• A sound is heard 5 s later than the lightning is seen in the sky on a rainy day.
• Find the distance of location of lightning?
• Given the speed of sound = 346 ms–1

Solution:

• Speed = Distance/ Time
• Distance = Speed × Time
• = 346 × 5 = 1730 m
• Thus, the distance of location of lightning is 1730 m.

Velocity

• Velocity is the rate of change of displacement.
• It is the displacement in unit time.
• It is a vector quantity.
• The SI unit of velocity is ms–1.
• Velocity = Displacement / Time taken

Acceleration

• Acceleration is the rate of change of velocity or it is the change of velocity in unit time.
• It is a vector quantity.
• The SI unit of acceleration is ms–2.
• Acceleration = Change in velocity/Time = (Final velocity – Initial velocity)/Time
• a = (v–u)/t
• Consider a situation in which a body moves in a straight line without reversing its direction.
• From the above equation if v > u, i.e. if final velocity is greater than initial velocity, the velocity increases with time and the value of acceleration is positive.
• If v < u, i.e. if final velocity is less than initial velocity, the velocity decreases with time and the value of acceleration is negative.
• It is called negative acceleration.
• Negative acceleration is called retardation or deceleration.
• If the acceleration has a value of –2 ms–2, we say that deceleration is 2 ms–2.

Graphical representation of motion along a straight line

• Plotting the distance/displacement or speed/velocity on a graph helps us to understand certain things about time and position.
• The distance – time graph for Uniform motion
• Consider the Table 2.1 which shows the distance walked by a person at different times.

Table 2.1 Uniform motion

Time (minute)	Distance (metre)
0	0
5	500
10	1000
15	1500
20	2000
25	2500

• A graph is drawn by taking time along X-axis and distance along Y-axis. The graph is known as distance – time graph.

• When we look at the distance – time graph, we notice few things.
• First, it is a straight line. We also notice that the person covers equal distances in equal intervals of time.
• We can therefore conclude that he walked at a constant speed.
• Can you find the speed at which he walked, from the graph?
• Yes, you can. The parameter is referred as the slope of the line.
• Speed = Distance covered / Time taken = Slope of the straight line = BC/AC (From the graph) = 500 / 5 = 100 m/min
• Steeper the slope (in other words the larger value) the greater is the speed. Let us take a look at the distance – time graphs of three different people – Asher walking, Saphira cycling and Kanishka going in a car, along the same path (Fig 2.3).
• We know that cycling can be faster than walking and a car can go faster than a cycle.
• The distance – time graph of the three would be as given in the following graph.
• The slope of the line on the distance – time graph becomes steeper and steeper as the speed increases.

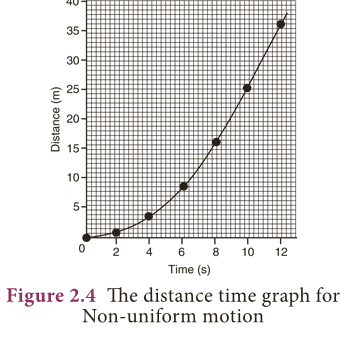
The distance time graph for Non-uniform motion

• We can also plot the distance – time graph for accelerated motion (non-uniform motion).
• Table 2.2 shows the distance travelled by a car in a time interval of two seconds.

Table 2.2 Non-uniform motion

Time (second)	Distance (metre)
0	0
2	1
4	4
6	9
8	16
10	25
12	36

• If we plot a graph between the distance travelled and the time taken, it would be as shown in Figure 2.4.
• Note that the graph is not a straight line as we got in the case of uniform motion.
• This nature of the graph shows non–linear variation of the distance travelled by the car with time.
• Thus, the graph represents motion with non- uniform speed.

Velocity – Time graph

• The variation in velocity of an object with time can be represented by velocity – time graph.
• In the graph, time is represented along the X – axis and the velocity is represented along the Y – axis.
• If the object moves at uniform velocity, a straight line parallel to X-axis is obtained.
• This graph shows the velocity – time graph for a car moving with uniform velocity of 40 km/hour.
• We know that the product of velocity and time gives displacement of an object moving with uniform velocity.
• Thus, the area under the velocity – time graph is equal to the magnitude of the displacement.

• So, the distance (displacement), S covered by the car in a time interval of t can be expressed as, S = AC × CD
• S = Area of the rectangle ABCD (shaded portion in the graph)
• We can also study about uniformly accelerated motion by plotting its velocity – time graph.
• Consider a car being driven along a straight road. Its velocity for every 5 seconds is noted from the speedometer of the car.
• The velocity of the car in ms–1 at different instants of time is shown in the Table 2.3.

Table 2.3 Uniformly accelarated motion

Time (Second)	Velocity of the Car (ms–1)
0	0
5	9
10	18
15	27
20	36
25	45
30	54

• In this case, the velocity – time graph for the motion of the car is shown in Figure 2.6 (straight line).
• The nature of the graph shows that the velocity changes by equal amounts in equal intervals of time.
• Thus, for all uniformly accelerated motion, the velocity – time graph is a straight line.

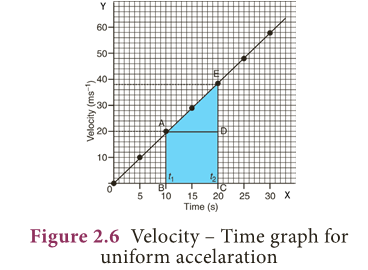
• One can also determine the distance moved by the car from its velocity – time graph.
• The area under the velocity – time graph gives the distance (magnitude of displacement) moved by the car in a given interval of time.
• Since the magnitude of the velocity of the car is changing due to acceleration, the distance, S travelled by the car will be given by the area ABCDE under the velocity – time graph.
• That is, S = Area ABCDE
• = Area of the rectangle ABCD + Area of the triangle ADE
• S = (AB × BC) + ½ (AD × DE)
• Area of the quadrangle ABCDE can also be calculated by calculating the area of trapezium ABCDE.
• It means, S = Area of trapezium ABCDE
• = ½ × Sum of length of parallel sides × Distance between parallel sides
• S = ½ × (AB + CE) × BC
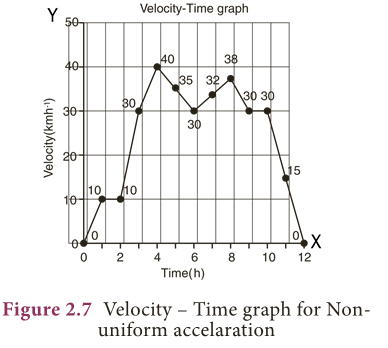
• In the case of non-uniformly accelerated motion, distance – time graph and velocity – time graphs can have any shape as shown in Figure 2.7.

Equations of Motion

• Newton studied the motion of an object and gave a set of three equations.
• These equations relate displacement, velocity, acceleration and time of an object under motion.
• An object in motion with initial velocity, u attains a final velocity, v in time, t due to acceleration, a and reaches a distance, s.
• Three equations can be written for this motion.
• v = u + at
• s = ut + ½ a t2
• v2 = u2 + 2as
• Let us try to derive these equations by graphical method.

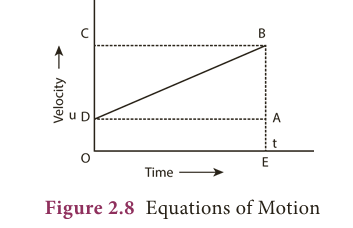
• Figure 2.8 shows the change in velocity with time for an uniformly accelerated object.
• The object starts from the point D in the graph with velocity, u.
• Its velocity keeps increasing and after time, t it reaches the point B on the graph.
• The initial velocity of the object = u = OD = EA
• The final velocity of the object = v = OC = EB
• Time = t = OE = DA
• From the graph we know that, AB = DC

First equation of motion

• By definition, Acceleration = Change in velocity / Time
• = (Final velocity – Initial velocity)/Time
• = (OC – OD) / OE
• = DC / OE a = DC / t
• DC = AB = at From the graph EB = EA + AB
• v = u + at
• This is the first equation of motion.

Second equation of motion

• From the graph the distance covered by the object during time, t is given by the area of quadrangle DOEB
• s = Area of the quadrangle DOEB
• = Area of the rectangle DOEA 0+ Area of the triangle DAB
• = (AE × OE) + (1/2 × AB × DA)
• s = ut + ½ at2

• This is the second equation of motion.

Third equation of motion

• We see that the distance covered by the object during time, t is given by the area of the quadrangle DOEB.
• Here, DOEB is a trapezium.
• Then,
• s = Area of trapezium DOEB
• = ½ × Sum of length of parallel side × Distance between parallel sides

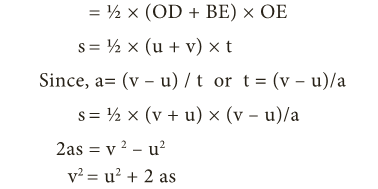
• = ½ × (OD + BE) × OE
• s = ½ × (u + v) × t
• Since, a= (v – u) / t or t = (v – u)/a
• s = ½ × (v + u) × (v – u)/a
• 2as = v 2 – u 2
• v2 = u 2 + 2 as
• This is the third equation of motion.

Problem 3

• The brakes applied to a car produce an acceleration of 6 ms–2 in the opposite direction to the motion.
• If the car takes 2 s to stop after the application of brakes, calculate the distance travelled during this time.
• Solution:
• We have been given a = –6 ms–2, t = 2s and v = 0
• From the equation of motion,
• v = u + at
• 0 = u + (‒6 × 2)
• 0 = u – 12
• ∴u = 12 ms‒1
• s = ut + ½ at2
• = (12 × 2) + ½ (–6 × 2 × 2)
• = 24 – 12 = 12m
• Thus, the car will move 12 m before it stops after the application of brakes.

Motion of freely falling body

Activity

• Take a large stone and a small eraser.
• Stand on the top of a table and drop them simultaneously from the same height.
• What do you observe?
• Now, take a small eraser and a sheet of paper. Drop them simultaneously from the same height. What do you observe?
• This time, take two sheets of paper having same mass and crumple one of the sheets into a ball.
• Now, drop the sheet and the ball from the same height. What do you observe?
• From Activity, you can observe that, both the stone and the eraser reach the surface of the earth almost at the same time.
• When you drop the eraser and paper, the eraser reaches first and the sheet of paper reaches later.
• You can also observe that the paper crumpled into a ball reaches ground first and plain sheet of paper reaches later, although they have equal mass.
• Do you know the reason?
• When all these objects are dropped in the absence of air medium (vacuum), all would have reached the ground at the same time.
• In air medium, air offers some resistance to the motion of freely falling objects.
• But, it is negligibly small when compared to the gravitational pull acting on the stone and rubber.
• Hence, they reach the ground at the same time. It can be seen from these activities that the magnitude of air resistance depends on the area of objects exposed to air.
• We know that an object experiences acceleration during free fall.
• This acceleration experienced by an object is independent of mass.
• This means that all objects hollow or solid, big or small, should fall at the same rate.
• The equation of motion for a freely falling body can be obtained by replacing ‘a’ in equations with g, the acceleration due to gravity.
• For a freely falling body which is initially at rest, u = 0.
• Thus we get the following equations. v = gt, s = ½ gt2, v2 = 2gh

• When we throw an object vertically upwards, it moves against the acceleration due to gravity.
• Hence, ‘a’ is taken to be –g and when moving downwards ‘a’ is taken as +g.

Uniform circular motion

Activity

• Take a piece of thread and tie a small piece of stone at one of its ends.
• Rotate the stone to describe a circular path with constant speed by holding the thread at the other end.
• Now, release the thread and let the stone go.
• Can you tell the direction in which the stone moves after it is released?
• If you carefully observe, on being released the stone moves along a straight line tangential to the circular path.
• This is because once the stone is released, it continues to move along the direction it has been moving at that instant.
• This shows that the direction of motion changes at every point when the stone was moving along the circular path.
• When an object is moving with a constant speed along a circular path, the velocity changes due to the change in direction.
• Hence, it is an accelerated motion.
• For example, revolution of earth around the sun, revolution of moon around the earth and the tip of the second’s hand of a clock are all accelarated motions.
• If an object, moving along a circular path of radius, r takes time, T to come back to its starting position, then the speed, v is given by, Speed = Circumference/Time taken

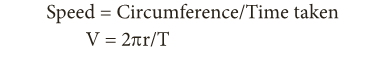
Centripetal Acceleration and Centripetal Force

• A body is said to be accelerated, if the velocity of the body changes either in magnitude or in direction.
• So, the motion of a stone in circular path with constant speed and continuous change of direction is an accelerated motion.
• In this case, there must be an acceleration acting along the string directed inwards, which makes the stone to move in circular path.

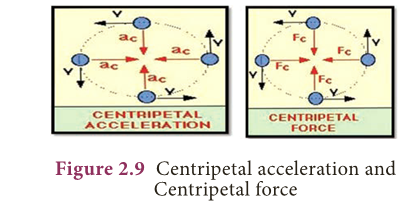
• This acceleration is known as centripetal acceleration and the force is known as centripetal force.
• Since the centripetal acceleration is directed radially towards the centre of the circle, the centripetal force must act on the object radially towards the centre.
• Let us consider an object of mass m, moving along a circular path of radius r, with a velocity, v.
• Its centripetal acceleration is given by a = v2 /r

• The magnitude of centripetal force is given by, F = Mass × Centripetal acceleration
• F = mv 2 /r

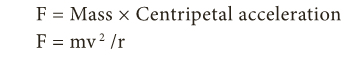
Problem

• A 900 kg car moving at 10 ms–1 takes a turn around a circle with a radius of 25 m. Determine the acceleration and the net force acting upon the car.
• Solution: When the car turns around circle, it experiences centripetal acceleration,
• a = υ 2 / r
• a=(10) /25 ^2 = 100 /25 = 4 ms–2 Net force acting upon the car,
• F = m a = 900 × 4 = 3600 N

Centrifugal Force

Activity

• Take a piece of rope and tie a small stone at one end.

• Hold the other end of the rope and rotate it such that the stone follows a circular path.
• Do you experience any pull or push in your hand?
• In this activity, a pulling force that acts away from the centre is experienced. This is called as centrifugal force.
• Force acting on a body away from the centre of circular path is called centrifugal force.
• Thus, centrifugal force acts in a direction which is opposite to the direction of centripetal force.
• Its magnitude is same as that of centripetal force.
• The dryer in a washing machine is an example for the application of centrifugal force.

EXTRA POINTS

• Motion: An object’s change in its position.
• Distance: Length an object has covered during its motion.
• Displacement: Change in the position of an object measuring from its starting position to the final position only.
• Speed: Rate of motion at which the object moves (distance/time).
• Velocity: Speed of an object in a particular direction.
• Acceleration: Change in magnitude or direction of velocity.
• Circular motion: Movement of an object along the circumference of a circle or rotation along a circular path.
• Centripetal force: Force which acts on a body moving in a circular path and directed towards the centre.
• Centrifugal force: Force, arising from the body’s inertia, which appears to act on a body moving in a circular path and is directed away from the centre.
• Gravity: Force of attraction between an object and the centre of Earth, due to their masses.

MORE TO KNOW:

The speedometer

• The speedometer of an automobile measures the instantaneous speed of the automobile.
• In a uniform motion in one dimension, the average velocity is equal to instantaneous velocity.
• Instantaneous velocity is also called velocity or instantaneous speed or simply speed.

Zero Velocity and Finite Acceleration

• Can a body have zero velocity and finite acceleration?
• Yes, when a body is thrown vertically upwards in space, at the highest point, the body has zero velocity but it has acceleration due to the gravity.

Centripetal Forces

• Any force like gravitational force, frictional force, magnetic force, electrostatic force etc., may act as a centripetal force.

Centrifugal Force

• When you go for a ride in a merry-go-round in amusement parks, you will experience an outward pull as merry-go round rotates about vertical axis.
• This is due to centrifugal force.