Measurement Notes 7th Science Lesson 1 Notes in English

7th Science Lesson 1 Notes in English

1] Measurement

Introduction:

• In day to day life, we measure many things such as the weight of fruits, vegetables, food grains, volume of liquids, temperature of the body, speed of the vehicles etc., Quantities such as mass, weight, distance, temperature, volume are called physical quantities.
• A value and a unit are used to express the magnitude of a physical quantity. For example Suresh walks 2 kilometer everyday.
• In this example ‘2’ is the value and ‘kilometer’ is the unit used to express the magnitude of distance which is a physical quantity.

Fundamental and derived quantities:

• Generally, physical quantities are classified into two types, namely,
• Fundamental quantities and (ii) Derived quantities.

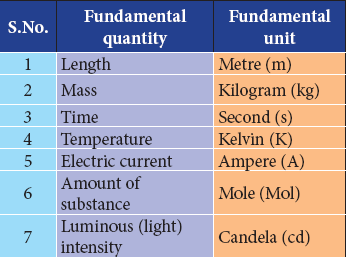
Fundamental quantities:

• A set of physical quantities which cannot be expressed in terms of any other quantities are known as “Fundamental quantities”. Their corresponding units are called “Fundamental units”.
• There are seven fundamental physical quantities in SI Units (System of International Units).

Derived quantities:

• All other physical quantities which can be obtained by multiplying, dividing or by mathematically combining the fundamental quantities are known as “derived quantities”.
• Their corresponding units are called “Derived units”. Some of the derived quantities and their units

Area:

The area is a measure of how much space there is on a flat surface.

The area of the plot of land is derived by multiplying the length and breadth

Area = length × breadth

The unit of the area is = metre × metre

= metre^2

= m^2 (Read as square metre)

Area is a derived quantity as we obtain are by multiplying twice of the fundamental physical quantity length.

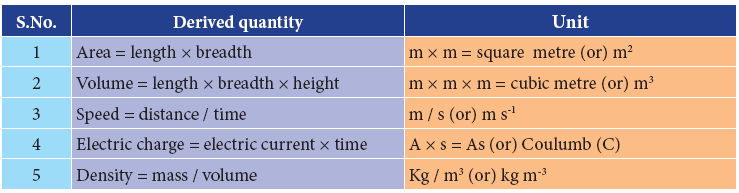
Some of the derived quantities and their units in SI System of units

Area of regularly shaped figures

• The area of regularly shaped figures can be calculated using the relevant formulae.

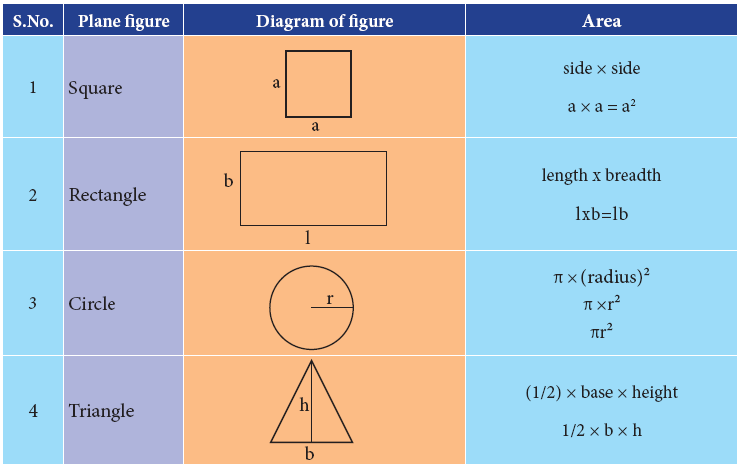
Area of some regularly shaped figures

Area of irregularly shaped figures

• In our daily life, we encounter many irregularly shaped figures like leaves, maps, stickers of stars or flowers, peacock feather etc.
• The area of such irregularly shaped figures cannot be calculated using any formula.
• We can find the area of these figures with the help of a graph sheet.
• The following activity shows how to find the area of irregularly shaped plane figures.
• The graphical method explained above can be used to find the area of regularly shaped figures also. In the case of square and rectangle, this method gives the area accurately.

Volume

• The amount of space occupied by a three dimensional object is known as its volume.
  • • Volume = surface area × height
• The SI unit of volume is cubic metre or m^3.

Volume of regularly shaped objects

• As in the case of area, the volume of the regularly shaped objects can also be determined using an appropriate formula
• The formulae used to calculate the volume of these regularly shaped objects.

Volume of liquids

• Liquids also occupy some space and hence they also have volume.
• But, liquids do not possess any definite shape. So, the volume of a liquid cannot be determined as in the case of solids.
• When a liquid is poured into a container, it takes the shape and volume of the container.
• The volume of any liquid is equal to the space that it fills and it can be measured using a measuring cylinder or measuring beaker.
• The maximum volume of liquid that a container can hold is known as the “capacity of the container”. A measuring container is graduated.
• The volume of a liquid is equal to the volume of space it fills in the container. This can be directly observed from the readings marked in the measuring containers.
• If we notice the measuring cups given in figure carefully, we can observe that the readings are marked in the unit of “ml”. This actually represents millilitre.
• To understand this unit of volume, let us first understand how much a litre means.
• Litre is the commonly used unit to measure the volume of liquids.
• We can understand that the unit of volume is cubic cm if the dimensions of the object are given in cm.
• This cubic cm is commonly known as cc. A volume of 1000 cc is termed as one litre (l).

1 litre = 1000 cc or cm^3

1000 ml = 1 litre

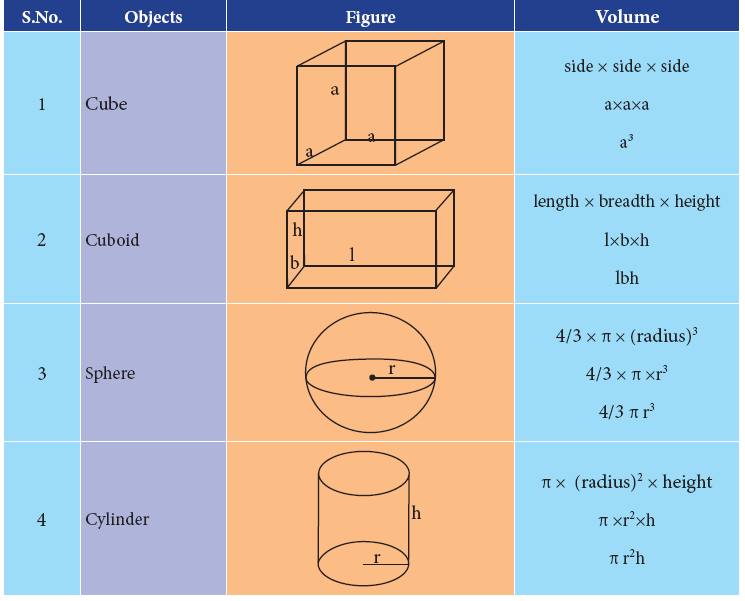
Volume of irregularly shaped objects

• As we discussed earlier for the case of area, there are no formulae to determine the volume of irregularly shaped objects.
• For such cases, their volume can be determined using a measuring cylinder and water.

Density

• The lightness or heaviness of a body is due to density.
• If more mass is packed into the same volume, it has greater density. So, the iron block will have more mass than the wooden block of the same size. Therefore iron has more density.

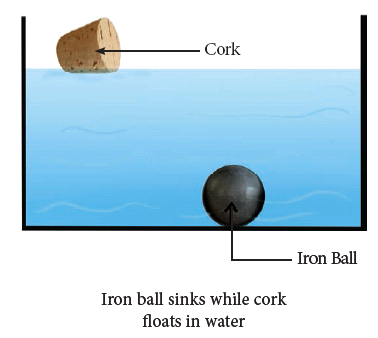
Definition of density:

• Density of a substance is defined as the mass of the substance contained in unit volume (1 m^3).
• If the mass of a substance is “M” whose volume is “V”, then, the equation for density is given as

Density (D) =mass (M)/volume (V)

D =M/V

Unit of density

• SI unit of density is kg/m^3. The CGS unit of density is g/cm^3.

Density of different materials

• Different materials have different densities. The materials with higher density are called “denser” and the materials with lower density are called “rarer”.
• The density of some widely used materials is listed.

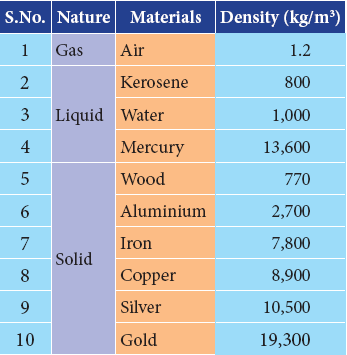
Density of some common substances, at room temperature

Measuring distance of celestial bodies

• Normally, we use centimeter, metre and kilo metre to express the distances that we measure in our day to day life.
• But, for space research, astronomers need to measure very long distances such as the distance between the earth and a star or the distance between two stars. To express these distances, we shall learn about two such units, namely,

i. Astronomical unit

ii. Light year

Astronomical unit

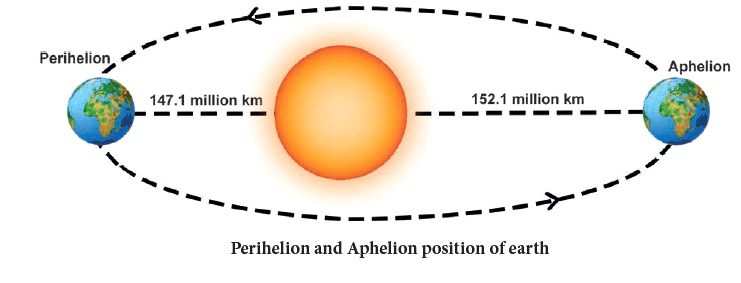
• We all know that the earth revolves around the sun in an elliptical orbit. Hence, the distance between the sun and the earth varies every day.
• When the earth is in its perihelion position (Perihelion is position of the shortest distance between the earth and the sun), the distance between the earth and the sun is about 147.1 million kilometre.
• When the earth is in its farthest position, that is when the distance between Earth and Sun is the largest (called aphelion position) the distance is 152.1 million kilometer.
• The average distance between the earth and the sun is about 149.6 million kilometer. This average distance is taken as one astronomical unit.
• Neptune is 30 AU away from the Sun. It means it is thirty times farther than the Earth.
• One astronomical unit is defined as the average distance between the earth and the sun.

1 AU = 149.6 million km = 149.6 × 10^6 km

= 1.496 × 10^11 m

Light year

• The nearest star to our solar system is Proxima Centauri. It is at a distance of 2, 68,770 AU. We can clearly see that using the AU for measuring distances of stars would be unwieldy.
• Therefore, astronomers use a special unit, called ‘light year’, for measuring the distance in deep space. We have learnt that the speed of light in vacuum is 3 × 10^8m/s.
• This means that light travels a distance of 3 × 10^8 m in one second. In a year (non-leap), there are 365 days.
• Each day has 24 hours; each hour has 60 minutes; each minute has 60 seconds. Thus, the total number of seconds in one year = 365 × 24 × 60 × 60 = 3.153 × 10^7 second
• If light travels a distance of 3 × 108 m in one second, then the distance travelled by light in one year = 3 × 10^8 × 3.153 × 10^7 = 9.46 × 10^15 m. This distance is known as one light year.
• One light year is defined as the distance travelled by light in vacuum during the period of one year.

1 Light year = 9.46 × 10^15 m.

• In terms of light year, Proxima Centauri is at 4.22 light-years from Earth and the Solar System (and Earth). The Earth is located about 25,000 light-years away from the galactic center.

More to know:

• One square metre is the area enclosed inside a square of side 1 metre.
• To measure the volume of liquids, some other units are also used. Some of them are gallon, ounce, and quart.

1 gallon = 3785 ml

1 ounce = 30 ml

1 quart = 1 litre

• Water has more density than oils like cooking oil and castor oil, although these oils appear to be denser than water.
• Density of castor oil is 961 kg/m^3. If we put one drop of water in oil, water drop sinks.
• But, if we put one drop of oil in water, oil floats and forms a layer on water surface. However, some oils are denser than water.