Force And Motion Notes 7th Science Lesson 2 Notes in English

7th Science Lesson 2 Notes in English

2] Force And Motion

Introduction

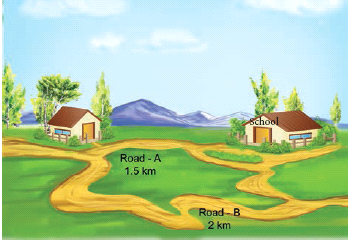
• We could conclude that when an object travel from one place to another, it will reach faster if it travels along the straight line path.
• The straight line path is the shortest distance between two points.

Distance and Displacement

Distance

• The total length of a path taken by an object to reach one place from the other is called distance.

Displacement

• The shortest distance from the initial to the final position of an object.
• Both the distance and displacement posses the same unit. The SI unit is meter (m).

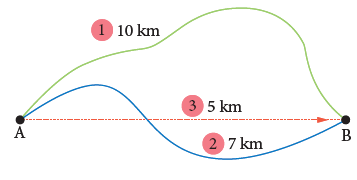
• Figure shows the motion of a person between two places A and B.
• He travels 10 km in first path. In the second path, he travels 7 km.
• The distance between A and B via first path is 10 km. In the second path the distance is 7 km.
• The shortest distance between the two places is 5 km represented as 2. So the displacement is 5 km. (In east direction)
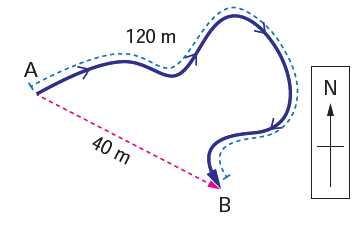
• The path of an object travelling from A to B is shown in figure.
• Total distance travelled by the object is 120 m. The displacement of the object is 40 m (south-east direction)

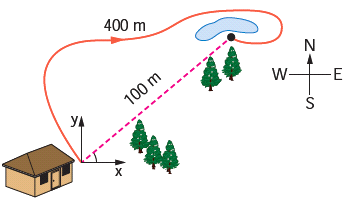
• When we represent the displacement, we use a positive or negative sign depending on the direction with which it travels.

• Here we can consider the starting point as A and while the object moves from A to B the displacement is considered to be positive and from B to A it is negative.

Speed – Velocity

Speed

Recapitulation

• Speed is the rate of change of distance.
• Speed = distance /time
• Unit is metre/second (m/s)

We can classify speed into two types.

Uniform speed

• If a body in motion covers equal distances in equal intervals of time, then the body is said to be in uniform speed.

Non- uniform speed

• If a body covers unequal distances in equal intervals of time, the body is said to be in non- uniform speed.

Average speed = total distance travelled /time taken to travel the distance.

Velocity

• Velocity is the rate of change in displacement.

Velocity (v) = displacement / time

SI unit of velocity is meter / second (m/s)

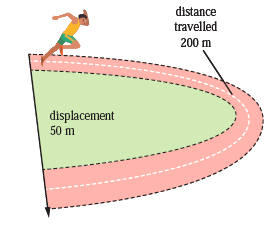
• If an athlete in the diagram takes 25 s to complete a 200 m sprint event. Find her speed and velocity.

Speed = distance / time

= 200 / 25

= 8 m/s

Velocity = displacement /time

= 50 / 25

= 2 m/s

Uniform velocity

• A body has uniform velocity, if it covers equal displacement in the same direction in equal intervals of time. E.g. light travels through vacuum.

Non uniform velocity

• If either speed or direction changes, the velocity is non uniform. E.g. a train starting and moving out of the station.

Average velocity

Average velocity = total displacement /total time taken

• E.g. Figure shows a car that travels 5 km due east and makes a U – turn to travel another 7 km. If the time taken for the whole journey is 0.2 h. calculate the average velocity of the car.

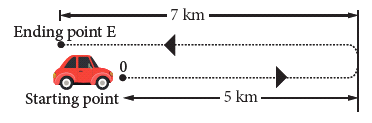
• Average velocity = total displacement/time taken.(taking the direction due east of point O as positive)

= (5 – 7) / 0.2

= –2 / 0.2

= –10 km/h (or) –10 × 5/18 = 25/9

= –0.28 m / s

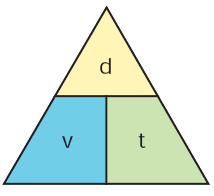
• The triangle method can help you to recall the relationship between velocity (v), displacement (d), and time (t).

v = d / t , t = d / v, d = v × t

Acceleration

Acceleration (a)

• Acceleration is the rate of change in velocity. In other words if a body changes its speed or direction then it is said to be accelerated.

Acceleration = change in velocity/ time = [final velocity (v) – intial velocity (u)] / time (t)

a = (v–u) / t

• SI unit of acceleration is m/s^2
• In other words, the object undergoes acceleration when its speed and/or direction change(s).

Tell me

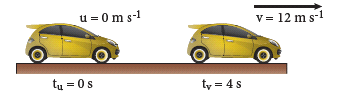
• A car at rest starts to travel in a straight path. It reaches a velocity of 12 m/s in 4 s . What is its acceleration. Assuming that it accelerates uniformly?

Initial velocity u = 0 m/s (since the car starts from rest)

Final velocity (v) = 12 m /s

Time taken (t) = 4 s

Acceleration (a) = (v – u) / t

= (12 – 0) / 4

= 3 m / s^2

Positive acceleration

• If the velocity of an object increases with respect to time, then the object is said to be in positive acceleration or just acceleration.

Negative acceleration or deceleration or retardation

• If the velocity of an object decreases with respect to time, then the object is said to be in negative acceleration or deceleration or retardation.

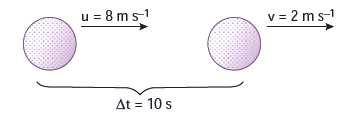
• The velocity of a golf ball rolling in a straight line changes from 8 m/s to 2 m/s in 10 s. What is its deceleration, assuming that it is decelerating uniformly?

Initial velocity (u) = 8 m/s

Final velocity (v) = 2 m/s

Time taken (t) = 10 s

Acceleration (a) = (v – u)/t

= (2 – 8)/10

= –0.6 m/s^2

The deceleration is –0.6 m/s^2

Uniform acceleration

• An object undergoes uniform acceleration when the change (increase or decrease) in its velocity for every unit of time is the same.

Table shows a moving bus with uniform acceleration.

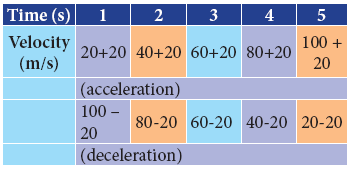
• When the velocity of the object is increasing by 20 m/s the acceleration is 20 m/s^2.
• When the velocity of the object is decreasing by 20 m/s the deceleration is 20 m/s^2.

Non – uniform acceleration

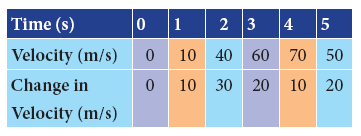
• An object undergoes non uniform acceleration if the change in its velocity for every unit of time is not the same.
• Note that the change in velocity is not the same for every second. The moving object is undergoing non uniform acceleration.

Distance – Time Graphs

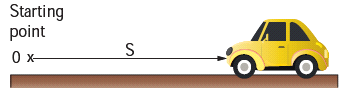
• Figure shows a car travelling along a straight line away from the starting point O.
• The distance of the car is measured for every second. The distance and time are recorded and a graph is plotted using the data. The results for four possible journeys are shown below.

Speed – time graphs

• Let us consider a bus travelling from Thanjavur to Trichy.
• The speed of the bus is measured for every second. The speed and time are recorded and a graph is plotted using the data. The results for four possible journeys are shown.

Comparisons between distance – time and speed – time graphs

• Speed – time graphs and Distance – time graphs look very similar, but they give different information. We can differentiate them by looking at the labels.

Centre of Gravity and Stability

Centre of gravity

• We observe there is only one point which the cardboard is balanced. The point which the cardboard is balanced is called the centre of gravity of the cardboard.

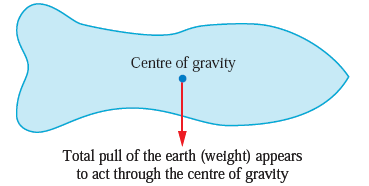
Centre of gravity:

• The centre of gravity of an object is the point through which the entire weight of the object appears to act.

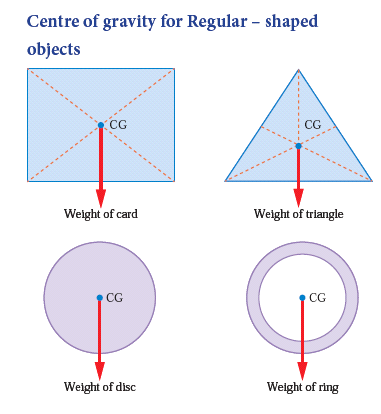
• Generally the centres of gravity of the geometrical shaped object lie on the geometric centre of the object.
• Examples of centre of gravity for Regular- shaped objects. 1. Weight of Card, 2. Weight of Triangle, 3. Weight of Disc, 4. Weight of Ring.

What about irregular shaped objects?

• Apparatus : Irregularly shaped card, string, pendulum bob, stand
• Make three holes in the lamina.
• Suspend the lamina from the optical pin through one of the holes as shown.
• Suspend the plumbline from the pin and mark the position of the plumbline on the lamina.
• Draw lines on the lamina representing the positions of the plumbline.
• Repeat the above steps for the holes.
• Label the intersection of the three lines as X, the position of the centre of gravity of the lamina.

Meter Rule

• The ruler is in equilibrium when supported at its centre of gravity.

• For a regular object such as a uniform meter rule, the centre of gravity is at the centre of the object. When the object is supported at that point, it will be balanced.
• If it is supported at any other point, it will topple.

Stability

• Stability is a measure of the body’s ability to maintain its original position.
• The three types of stability are

(a) Stable equilibrium

(b) Unstable equilibrium

(c) Neutral equilibrium

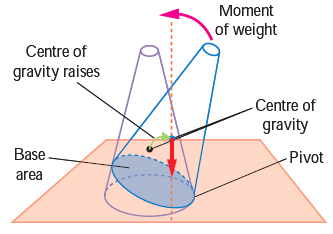
Stable Equilibrium

• The frustum can be tilted through quite a big angle without toppling.
• Its centre of gravity is raised when it is displaced.
• The vertical line through its centre of gravity still falls within its base. So it can return to its original positional.

Unstable Equilibrium

• The frustum will topple with the slightest tilting. Its centre of gravity is lowered when it is displaced.

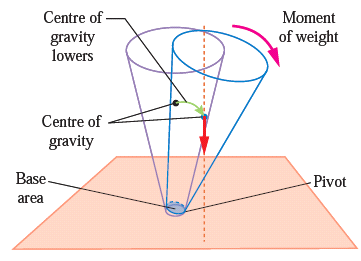
• The vertical line through its centre of gravity falls outside its base.

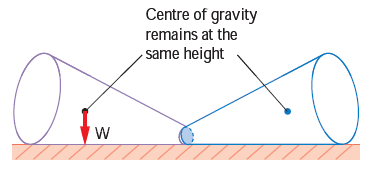
Neutral Equilibrium

(d) It causes frustum to topple.

(e) The frustum will rolls about but does not topple.

(f) Its centre of gravity remains at the same height when it is displaced.

(g) The body will stay in any position to which it has been displaced.

Condition for Stability

• To make a body more stable
• Lower its centre of gravity
• Increase the area of its base ™
• This box is at the point of tipping over
• A heavy base lowers at the centre of gravity
• So the box does not tip over
• A brode base makes the box more difficult to tip over

The Thanjavur Doll

• It is s type of traditional Indian toy made of terracotta material.
• The centre of gravity and the total weight of the doll is concentrated at its bottom most point, generating a dance-like continuous movement with slow oscillations.

Real Life Applications of Centre of Gravity

• It is for the reasons of stability that the luggage compartment of a tour bus is located at the bottom and not on the roof.
• Extra passengers are not allowed on the upper deck of a crowded double decker bus.
• Racing cars are built low and broad for stability. Table lamps and fans are designed with large heavy bases to make them stable.

Science Today

Typical Speeds

Tortoise 0.1 m/s

Person walking 1.4 m / s

Falling raindrop 9-10 m / s

Cat running 14 m/s

Cycling 20-25 km/h

Cheetah running 31 m/s

Bowling speed of fast bowlers 90-100 miles /h

Badminton smash 80-90 m/s

Passenger jet 180 m/s

More to know:

Nautical mile

• Nautical mile is the unit for measuring the distance in the field of aviation and sea transportation. One nautical mile is 1.852 km.
• The unit for measuring the speed of aeroplanes and ships is knot. One knot is the speed taken to travel one nautical mile in hour.
• 1 km/h = 5/18 m/s

How we got this?

1 km = 1000 m

1 h = 3600 s

1 km / h = 1000 m / 3600 s = 5/ 18 m /s

• cheetah – 25 m/s to 30 m/s. My speed changes from 0 to 20 m/s in 2 second.