Fluids Notes 9th Science Lesson 3 Notes in English

Fluids Notes 9th Science Lesson 3 Notes in English

Introduction

• A small iron nail sinks in water, whereas a huge ship of heavy mass floats on sea water.
• Astronauts have to wear a special suit while travelling in space.
• All these have a common reason called ‘pressure’.
• If the pressure increases in a solid, based on its inherent properties, it experiences tension and ultimately deforms or breaks.
• In the case of fluids it causes them to flow rather than to deform.
• Although liquids and gases share some common characteristics, they have many distinctive characteristics on their own.
• It is easy to compress a gas whereas liquids are incompressible. Learning of all these facts helps us to understand pressure better.
• In this lesson you will study about pressure in fluids, density of fluids and their application in practical life.

Thrust and Pressure

• Pushing a pin into a board by its head is difficult. But pushing it by the pointed end is easy. Why? Have you ever wondered
• Why a camel can run in a desert easily? Why a truck or a motorbus has wider tyre? Why cutting tools have sharp edges?
• In order to answer these questions and understand the phenomena involved, we need to learn about two interrelated physical concepts called thrust and pressure.

Activity 1

• Stand on loose sand. Your feet go deep into the sand.
• Now, lie down on the sand. What happens? You will find that your body will not go that deep into the sand. Why?
• In both the cases of the above activity, the force exerted on the sand is the weight of your body which is the same.
• This force acting perpendicular to the surface is called thrust.
• When you stand on loose sand, the force is acting on an area equal to the area of your feet.
• When you lie down, the same force acts on an area of your whole body, which is larger than the area of your feet.
• Therefore, the effect of thrust, depends on the area on which it acts.
• The effect of thrust on sand is larger while standing than while lying. The force per unit area acting on an object concerned is called pressure.
• Thus, we can say thrust on an unit area is pressure.

• For the same given force, if the area is large pressure is low and vice versa. This is shown in Figure 3.1.

• In SI units, the unit of thrust is newton (denoted as N).
• The unit of pressure is newton per square metre or newton metre–2 (denoted as Nm–2).
• In the honour of the great French scientist, Blaise Pascal, 1 newton per square metre is called as 1 pascal denoted as Pa. 1 Pa = 1 N m–2

Problem 1

• A man whose mass is 90 kg stands on his feet on a floor. The total area of contact of his two feet with the floor is 0.036 m2 (Take, g = 10 ms–2).
• How much is the pressure exerted by him on the floor?
• Solution: The weight of the man (thrust), F = mg = 90 kg × 10 m s–2 = 900 N Pressure, P = F A = 900 N 0.036 m2 = 25000 Pa

Pressure in Fluids

• All the flowing substances, both liquids and gases are called fluids.
• Like solids, fluids also have weight and therefore exert pressure.
• When filled in a container, the pressure of the fluid is exerted in all directions and at all points of the fluid.
• Since the molecules of a fluid are in constant, rapid motion, particles are likely to move equally in any direction.

• Therefore, the pressure exerted by the fluid acts on an object from all directions.
• It is shown in Figure 3.2. Pressure in fluids is calculated as shown below.

• We shall first learn about the pressure exerted by liquids and then learn about the pressure exerted by gases.

Pressure due to liquids

• The force exerted due to the pressure of a liquid on a body submerged in it and on the walls of the container is always perpendicular to the surface.
• In Figure 3.3(a), we can see the pressure acting on all sides of the vessel.
• When an air filled balloon is immersed inside the water in a vessel it immediately comes up and floats on water.

• This shows that water (or liquid) exerts pressure in the upward direction. It is shown in Figure 3.3(b).
• Similarly, liquid pressure acts in lateral sides also.
• When a bottle having water is pierced on the sides we can see water coming out with a speed as in Figure 3.3(c).
• This is because liquid exerts lateral pressure on the walls the container.

Activity 2

• Take a transparent plastic pipe. Also take a balloon and tie it tightly over one end of the plastic pipe.
• Pour some water in the pipe from the top. What happens?
• The balloon tied at the bottom stretches and bulges out.
• It shows that the water poured in the pipe exerts a pressure on the bottom of its container.

Factors determining liquid pressure in liquids

• Pressure exerted by a liquid at a point is determined by,

1. depth (h)
2. density of the liquid (?)
3. acceleration due to gravity (g).

Activity 3

• Take a large plastic can. Punch holes with a nail in a vertical line on the side of the can as shown in figure.
• Then fill the can with water.

• The water may just dribble out from the top hole, but with increased speed at the bottom holes as depth causes the water to squirt out with more pressure.
• From this activity we can infer that pressure varies as depth increases.
• But, it is same at a particular depth independent of the direction.

Activity 4

• Take two liquids of different densities say water and oil to a same level in two plastic containers.

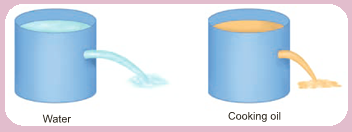
• Make holes in the two containers at the same level. What do you see? It can be seen that water is squirting out with more pressure than oil.
• This indicates that pressure depends on density of the liquid.

Pressure due to a liquid column

• A tall beaker is filled with liquid so that it forms a liquid column. The area of cross section at the bottom is A.
• The density of the liquid is?
• The height of the liquid column is h. In other words the depth of the water from the top level surface is ‘h’ as shown in Figure 3.4.

• We know that, thrust at the bottom of the column (F) = weight of the liquid. Therefore, F = mg (1)

• This expression shows that pressure in a liquid column is determined by depth, density of the liquid and the acceleration due to gravity.
• Interestingly, the final expression for pressure does not have the term area A in it.
• Thus, pressure in liquid depends on depth only.

Atmospheric pressure

• Earth is surrounded by a layer of air up to certain height (nearly 300 km) and this layer of air around the earth is called atmosphere of the earth.
• Since air occupies space and has weight, it also exerts pressure. This pressure is called atmospheric pressure.
• The atmospheric pressure we normally refer is the air pressure at sea level.

• Figure 3.5 shows that air gets ‘thinner’ with increasing altitude.
• Hence, the atmospheric pressure decreases as we go up in mountains.
• On the other hand air gets heavier as we go down below sea level like mines.

Measurement of atmospheric pressure

• The instrument used to measure atmospheric pressure is called barometer.
• A mercury barometer, first designed by an Italian Physicist Torricelli, consists of a long glass tube (closed at one end, open at the other) filled with mercury and turned upside down into a container of mercury.
• This is done by closing the open end of the mercury filled tube with the thumb and then opening it after immersing it in to a trough of mercury (Fig. 3.6).
• The barometer works by balancing the mercury in the glass tube against the outside air pressure.
• If the air pressure increases, it pushes more of the mercury up into the tub and if the air pressure decreases, more of the mercury drains from the tube.

• As there is no air trapped in the space between mercury and the closed end, there is vacuum in that space.
• Vacuum cannot exert any pressure. So the level of mercury in the tube provides a precise measure of air pressure which is called atmospheric pressure.
• This type of instrument can be used in a lab or weather station.
• On a typical day at sea level, the height of the mercury column is 760 mm.
• Let us calculate the pressure due to the mercury column of 760 mm which is equal to the atmospheric pressure.
• The density of mercury is 13600 kg m–3.

Problem 3

Gauge pressure and absolute pressure

• Our daily activities are happening in the atmospheric pressure.
• We are so used to it that we do not even realise.
• When tyre pressure and blood pressure are measured using instruments (gauges) they show the pressure over the atmospheric pressure.
• Hence, absolute pressure is zero-referenced against a perfect vacuum and gauge pressure is zero- referenced against atmospheric pressure.

• For pressures higher than atmospheric pressure, absolute pressure = atmospheric pressure + gauge pressure
• For pressures lower than atmospheric pressure, absolute pressure = atmospheric pressure – gauge pressure
• We have seen that liquid column exerts pressure.
• So the pressure inside the sea will be more. This is more than twice the atmospheric pressure.
• Parts of our body, especially blood vessels and soft tissues cannot withstand such high pressure.
• Hence, scuba divers always wear special suits and equipment to protect them (Fig. 3.7).

Pascal’s Law

• Pascal’s principle is named after Blaise Pascal (1623-1662), a French mathematician and physicist.
• The law states that the external pressure applied on an incompressible liquid is transmitted uniformly throughout the liquid.
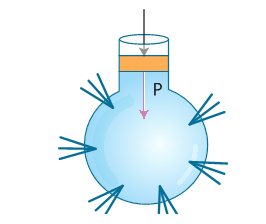
• Pascal’s law can be demonstrated with the help of a glass vessel having holes all over its surface. Fill it with water.
• Push the piston. The water rushes out of the holes in the vessel with the same pressure. The force applied on the piston exerts pressure on water.

DEMONSTRATION OF PASCAL’S LAW

• This pressure is transmitted equally throughout the liquid in all directions (Fig. 3.8).
• This principle is applied in various machines used in our daily life.

Hydraulic press

• Pascal’s law became the basis for one of the important machines ever developed, the hydraulic press.
• It consists of two cylinders of different cross-sectional areas as shown in Figure 3.9.
• They are fitted with pistons of cross-sectional areas “a” and ‘A’. The object to be lifted is placed over the piston of large cross-sectional area A.
• The force F1 is applied on the piston of small cross-sectional area ‘a’.
• The pressure P produced by small piston is transmitted equally to large piston and a force F2 acts on A which is much larger than F1.

• Pressure on piston of small area ‘a’ is given by, P = F1/ A1 (1)
• Applying Pascal’s law, the pressure on large piston of area A will be the same as that on small piston.
• Therefore, P = F2/ A2 (2)
• Comparing equations (1) and (2), we get F1/ A1 = F2 /A2. or F2 = F1 × A2/ A1

• Since, the ratio A2/ A1 is greater than 1, the force F2 that acts on the larger piston is greater than the force F1 acting on the smaller piston.
• Hydraulic systems working in this way are known as force multipliers.

Problem 4

• A hydraulic system is used to lift a 2000 kg vehicle in an auto garage.
• If the vehicle sits on a piston of area 0.5 m2, and a force is applied to a piston of area 0.03 m2, what is the minimum force that must be applied to lift the vehicle?
• Given: Area covered by the vehicle on the piston A1 = 0.5 m2
• Weight of the vehicle, F1 = 2000 kg × 9.8 m s–2 Area on which force F2 is applied, A2 = 0.03 m2
• Solution: P1 = P2 ; F1/ A1 = F2/ A2 and F2 = F1/ A1 x A2 ;
• F2 = (2000 × 9.8) 0.03 0.5 = 1176 N

Density

Activity 5

• Take two identical flasks and fill one flask with water to 250 cm3 mark and the other with kerosene to the same 250 cm3 mark.
• Measure them in a balance. The flask filled with water will be heavier than the one filled with kerosene.

• Why? The answer is in finding the mass per unit volume of kerosene and water in respective flasks.
• To understand density better, let us assume that the mass of the flask be 80 g. So, the mass of the flask filled with water is 330 g and the mass of flask filled with kerosene is 280 g.
• Mass of water only is 250 g and kerosene only is 200 g.
• Mass per unit volume of water is 250/250 cm3. This is 1g/cm3. Mass per unit volume of kerosene is 200 g/250 cm3. This is 0.8 g/cm3.
• The result 1 g/cm3 and 0.8 gcm3 are the densities of water and kerosene respectively.
• Therefore, the density of a substance is the mass per unit volume of a given substance.

Relative Density

• We can compare the densities of two substances by finding their masses.
• But, generally density of a substance is compared with the density of water at 4 °C because density of water at that temperature is 1g/cm3.
• Density of any other substance with respect to the density of water at 4 °C is called the relative density.

• Thus relative density of a substance is defined as ratio of density of the substance to density of water at 4 °C.

Measurement of relative density

• Relative density can be measured using Pycnometer also called density bottle.
• It consists of ground glass stopper with a fine hole through it.
• The function of the hole in a stopper is that, when the bottle is filled and the stopper is inserted, the excess liquid rises through the hole and runs down outside the bottle.
• By this way the bottle will always contain the same volume of whatever the liquid is filled in, provided the temperature remains constant.
• Thus, the density of a given volume of a substance to the density of equal volume of referenced substance is called relative density or specific gravity of the given substance.
• If the referenced substance is water then the term specific gravity is used.

Floating and sinking

• Whether an object will sink or float in a liquid is determined by the density of the object compared to the density of the liquid.
• If the density of a substance is less than the density of the liquid it will float.
• For example a piece of wood which is less dense than water will float on it.
• Any substance having more density than water (for example, a stone), will sink into it.

Problem 5

• You have a block of a mystery material, 12 cm long, 11 cm wide and 3.5 cm thick. Its mass is 1155 grams.
• (a) What is its density?
• (b) Will it float in a tank of water, or sink?
• Solution: (a) Density = Mass Volume = 1155g 12 cm × 11 cm × 3.5 cm = 1155 g 462 cm3 = 2.5 g cm–3
• (b) The mystery material is denser than the water. So it sinks.

Application of principle of flotation

Hydrometer

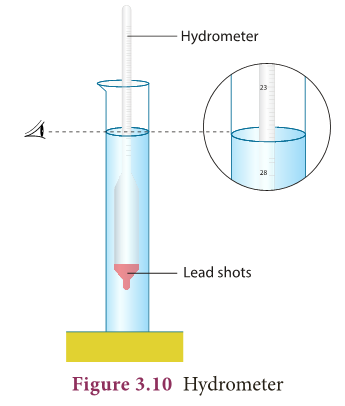
• A direct-reading instrument used for measuring the density or relative density of the liquid is called hydrometer.
• Hydrometer is based on the principle of flotation, i.e., the weight of the liquid displaced by the immersed portion of the hydrometer is equal to the weight of the hydrometer.
• Hydrometer consists of a cylindrical stem having a spherical bulb at its lower end and a narrow tube at its upper end.
• The lower spherical bulb is partially filled with lead shots or mercury. This helps hydrometer to float or stand vertically in liquids.
• The narrow tube has markings so that relative density of a liquid can be read directly.
• The liquid to be tested is poured into the glass jar. The hydrometer is gently lowered in to the liquid until it floats freely.
• The reading against the level of liquid touching the tube gives the relative density of the liquid.
• Hydrometers may be calibrated for different uses such as lactometers for measuring the density (creaminess) of milk, saccharometer for measuring the density of sugar in a liquid and alcoholometer for measuring higher levels of alcohol in spirits.

Lactometer

• One form of hydrometer is a lactometer, an instrument used to check the purity of milk.
• The lactometer works on the principle of gravity of milk.
• The lactometer consists of a long graduated test tube with a cylindrical bulb with the graduation ranging from 15 at the top to 45 at the bottom.
• The test tube is filled with air. This air chamber causes the instrument to float.
• The spherical bulb is filled with mercury to cause the lactometer to sink up to the proper level and to float in an upright position in the milk.
• Inside the lactometer there may be a thermometer extending from the bulb up into the upper part of the test tube where the scale is located.
• The correct lactometer reading is obtained only at the temperature of 60 °F. A lactometer measures the cream content of milk.
• More the cream, lower the lactometer floats in the milk.
• The average reading of normal milk is 32. Lactometers are used at milk processing units and dairies.

Buoyancy

• We already saw that a body experiences an upward force due to the fluid surrounding, when it is partially or fully immersed in to it.
• We also know that pressure is more at the bottom and less at the top of the liquid.
• This pressure difference causes a force on the object and pushes it upward.
• This force is called buoyant force and the phenomenon is called buoyancy (Fig.3.11).

• Most buoyant objects are those with a relatively high volume and low density.
• If the object weighs less than the amount of water it has displaced (density is less), buoyant force will be more and it will float (such object is known as positively buoyant).
• But, if the object weighs more than the amount of water it has displaced (density is more), buoyant force is less and the object will sink (such object is known as negatively buoyant).

Cartesian diver

• Cartesian diver is an experiment that demonstrates the principle of buoyancy. It is a pen cap with clay.
• The Cartesian diver contains just enough liquid that it barely floats in a bath of the liquid; its remaining volume is filled with air.
• When pressing the bath, the additional water enters the diver, thus increasing the average density of the diver, and thus it sinks.

Archimedes’ Principle

• Archimedes principle is the consequence of Pascal’s law.
• According to legend, Archimedes devised the principle of the ‘hydrostatic balance’ after he noticed his own apparent loss in weight while sitting in his bath.
• The story goes that he was so enthused with his discovery that he jumped out of his bath and ran through the town, shouting ‘eureka’.
• Archimedes principle states that ‘a body immersed in a fluid experiences a vertical upward buoyant force equal to the weight of the fluid it displaces’.
• When a body is partially or completely immersed in a fluid at rest, it experiences an upthrust which is equal to the weight of the fluid displaced by it.
• Due to the upthrust acting on the body, it apparently loses a part of its weight and the apparent loss of weight is equal to the upthrust.

• Thus, for a body either partially or completely immersed in a fluid,
• Upthrust = Weight of the fluid displaced = Apparent loss of weight of the body.
• Apparent weight of an object = True weight of an object in air – Upthrust (weight of water displaced)

Laws of flotation

• Laws of flotation are:

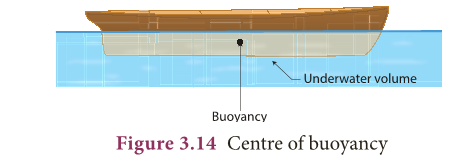
1. The weight of a floating body in a fluid is equal to the weight of the fluid displaced by the body.
2. The centre of gravity of the floating body and the centre of buoyancy are in the same vertical line.

• The point through which the force of buoyancy is supposed to act is known as centre of buoyancy. It is shown in Figure 3.14.

MORE TO KNOW:

FACT

• If a single nail pricks our body it is very painful. How is it possible for people to lie down on a bed of nails, still remain unhurt?
• It is because, area of contact is more.

HUMAN LUNG AND SEAS

• Human lung is well adapted to breathe at a pressure of sea level (101.3 k Pa).
• As the pressure falls at greater altitudes, mountain climbers need special breathing equipments with oxygen cylinders.
• Similar special equipments are used by people who work in mines where the pressure is greater than that of sea level.

PSI

• In petrol bunks, the tyre pressure of vehicles is measured in a unit called psi.
• It stands for pascal per inch, an old system of unit for measuring pressure.

SALT WATER

• Salt water provides more buoyant force than fresh water, because, buoyant force depends as much on the density of fluids as on the volume displaced.

MAGNESIUM

• Flotation therapy uses water that contains Epsom salts rich in magnesium.
• As a floater relaxes, he or she is absorbing this magnesium through the skin.
• Magnesium helps the body to process insulin, which lowers a person’s risk of developing Type 2 Diabetes.

EXTRA POINTS:

Altitude

• Vertical distance in the up direction.

Astronaut

• Person who is specially trained to travel into outer space.

Axes

• Simple machine to cut, shape and split wood.

Deformation

• Changes in an object’s shape or form due to the application of a force or forces.

Iceberg

• Large piece of ice floating in water.

Hydraulic systems

• Device that uses fluids and work under the fluid pressure to control valves.

Incompressible

• No change in volume if a pressure is applied.

Meteorological

• Weather condition.

Piston

• Movable disc fitted inside a cylinder.

Propellers

• Fan that transmits power in the form of thrust by rotation.

Syringe

• Simple pump made of plastic or glass to inject or withdraw fluid.

Therapy

• Treatment given for healing sickness. Velocity Speed of an objects with direction.