Atoms and Molecules Notes 10th Science Lesson 7 Notes in English

Atoms and Molecules

Introduction:

• Matter is made of atoms. Curiously the idea of atom was first proposed by the Greek philosophers in the fifth century BC (BCE).
• But, their theory was more philosophical than scientific. The first scientific theory of the atom was proposed by John Dalton.
• Few of the postulates of Dalton’s theory about an atom were found incorrect by the later on studies made by J.J. Thomson, Rutherford, Neils Bohr and Schrodinger.
• In the light of the result of the researches most of the limitations of the Dalton’s theory were removed and a new theory known as the modern atomic theory was put forward.

‘The main postulates of modern atomic theory’ are as follows:

• An atom is no longer indivisible (after the discovery of the electron, proton, and neutron).
• Atoms of the same element may have different atomic mass. (discovery of isotopes 17Cl35, 17Cl37).
• Atoms of different elements may have same atomic masses (discovery of Isobars 18Ar40, 20Ca40).
• Atoms of one element can be transmuted into atoms of other elements. In other words, atom is no longer indestructible (discovery of artificial transmutation).
• Atoms may not always combine in a simple whole number ratio (E.g. Glucose C6H12O6 C:H:O = 6:12:6 or 1:2:1 and Sucrose C12H22O11 C:H:O = 12:22:11).
• Atom is the smallest particle that takes part in a chemical reaction.
• The mass of an atom can be converted into energy (E = mc2).

The modern atomic theory is the basis for all the studies of chemical and physical processes that involve atoms. Atom and Atomic Mass:

• As you know, anything that has mass and occupies space is called matter. Atoms are the building blocks of matter.
• Since matter has mass, it must be due to its atoms. According to the modern atomic theory, an atom contains subatomic particles such as protons, neutrons and electrons.
• Protons and neutrons have considerable mass, but electrons don’t have such a considerable mass.
• Thus, the mass of an atom is mainly contributed by its protons and neutrons and hence the sum of the number of protons and neutrons of an atom is called its mass number.
• Individual atoms are very small and it is difficult to measure their masses. You can measure the mass of macroscopic materials in gram or kilogram. The mass of an atom is measured in atomic mass unit (amu).
• mass unit is one-twelfth of the mass of a carbon-12 atom; an isotope of carbon, which contains 6 protons and 6 neutrons. (Note: The symbol ‘amu’ is no longer used in the modern system and instead, it uses the symbol ‘u’ to denote unified atomic mass. The mass of a proton or neutron is approximately 1 amu).

Relative Atomic Mass (RAM)

• As an atom is very small, its absolute mass cannot be determined directly. The early pioneers of chemistry used to measure the atomic mass of an atom relative to an atom of another element.
• They measured the masses of equal number of atoms of two or more elements at a time, to determine their relative masses.
• They established one element as a standard, gave it an arbitrary value of atomic mass and using this value they measured the relative mass of other elements. The mass obtained by this way is called relative atomic mass.
• In the beginning, the mass of hydrogen atom was chosen as a standard and masses of other atoms were compared with it, because of the existence of isotopic character of hydrogen (1H1 , 1H2 , 1H3).
• Later hydrogen atom was replaced by oxygen atom as the standard. Now, the stable isotope of carbon (C-12) with atomic mass 12 is used as the standard for measuring the relative atomic mass of an element.
• Relative atomic mass of an element is the ratio between the average mass of its isotopes to 1/12th part of the mass of a carbon-12 atom. It is denoted as Ar. It is otherwise called “Standard Atomic Weight”.

Relative Atomic Mass

(Ar) = Average mass of the isotopes of the element/1/12thof the mass of one Carbon-12 atom

• Modern methods of determination of atomic mass by Mass Spectrometry use C-12 as standard.
• For most of the elements, the relative atomic mass is very closer to a whole number and it is rounded off to a whole number, to make calculations easier.

Relative atomic mass of elements (C-12 Scale)

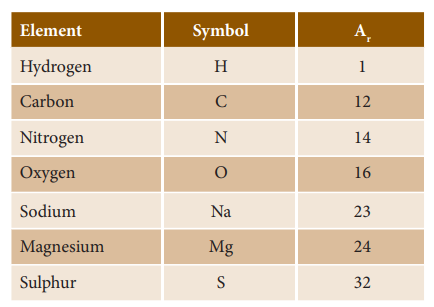
Average Atomic Mass (AAM)

• How can one measure the atomic mass of an element? It is somewhat more complicated because most of the naturally occuring elements exist as a mixture of isotopes, each of which has its own mass.
• Thus, it is essential to consider this isotopic mixture while calculating the atomic mass of an element.
• The average atomic mass of an element is the weighted average of the masses of its naturally occurring isotopes.
• But, the abundance of isotopes of each element may differ. So, the abundancy of all these isotopes are taken into consideration while calculating the atomic mass.
• Then, what do we mean by a weighted average? Let us consider an element which exists as a mixture of 50% of an isotope having a mass of 9 amu, and 50% of another isotope having a mass of 10 amu. Then, its average atomic mass is calculated by the following equation:

Average atomic mass

= (Mass of 1st isotope × % abundance of 1st isotope) + (Mass of 2nd isotope × % abundance of 2nd isotope)

Thus, for the given element the average

atomic mass = (9 × 50/100)+ (10 × 50/100 )

= 4.5 + 5 = 9.5 amu

(Note: In the calculations involving percentages, you need to convert percentage abundance into fractional abundance. For example, 50 percent is converted into 50/100 or 0.50 as shown in the a foresaid calculation.)

• The atomic masses of elements, given in the periodic table, are average atomic masses. Sometimes, the term atomic weight is used to mean average atomic mass.
• It is observed, from the periodic table that atomic masses of most of the elements are not whole numbers.
• For instance, the atomic mass of carbon given in the periodic table is 12.01 amu, not 12.00 amu.
• The reason is that while calculating the atomic mass of carbon, both of its natural isotopes such as carbon-12. and carbon-13 are considered.
• The natural abundance of C-12 and C-13 are 98.90 % and 1.10 % respectively. The average of the atomic mass of carbon is calculated as follows:

Average atomic mass of carbon

= (12 × 98.9/100 ) + (13 × 1.1/100)

= (12 × 0.989) + (13 × 0.011)

= 11.868 + 0.143 = 12.011 amu

So it is important to understand that if it is mentioned that the atomic mass of carbon is 12 amu, it refers to the average atomic mass of the carbon isotopes, not the mass of the individual atoms of carbon.

Molecule and Molecular Mass:

• Except noble gases, atoms of most of the elements are found in the combined form with itself or atoms of other elements. It is called as a molecule.
• A molecule is a combination of two or more atoms held together by strong chemical forces of attraction, i.e. chemical bonds.

Classification of molecules

• A molecule may contain atoms of the same element or may contain atoms of two or more elements joined in a fixed ratio, in accordance with the law of definite proportions.
• Thus, a molecule may be an element or a compound. If the molecule is made of similar kind of atoms, then it is called homoatomic molecule.
• The molecule that consist of atoms of different elements is called heteroatomic molecule. A compound is a heteroatomic molecule.
• The number of atoms present in the molecule is called its ‘atomicity’.

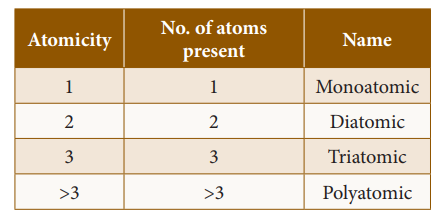
• Let us consider oxygen. Oxygen gas exists in two allotropic forms: Oxygen (O2) and Ozone (O3). In oxygen molecule, there are two oxygen atoms.
• So its atomicity is two. Since both the atoms are similar, oxygen (O2) is a homodiatomic molecule.
• Other elements that exist as diatomic molecules are hydrogen (H2), nitrogen (N2) and halogens: fluorine (F2), chlorine (Cl2), bromine (Br2) and iodine (I2).

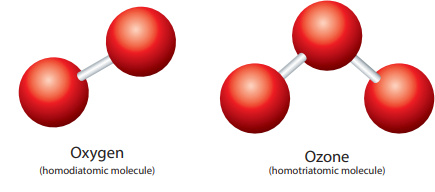
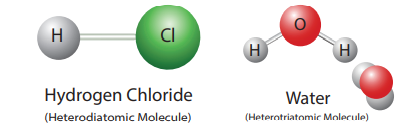
• Ozone (O3) contains three oxygen atoms and hence it is called homotriatomic molecule. If a molecule contains more than three atoms, then it is called polyatomic molecule. Conisder hydrogen chloride.
• It consists of two atoms, but of different elements, i.e. hydrogen and chlorine. So, its atomicity is two. It is a heterodiatomic molecule.
• Similarly, the water molecule contains two hydrogen atoms and one oxygen atom. So its atomicity is three. It is a heterotriatomic molecule.

Relative Molecular Mass (RMM)

• As the molecules are made of atoms, they also have their own mass. The mass of the molecule of an element or compound is measured in the C-12 scale and hence called relative molecular mass.
• The Relative Molecular Mass of a molecule is the ratio between the mass of one molecule of the substance to 1/12th mass of an atom of Carbon -12.
• The relative molecular mass is obtained by adding together the relative atomic masses of all the atoms present in a molecule.

Difference between atoms and molecules:

Even though atoms are the basic components of molecules, they differ in many aspects when compared to the molecules.

Mole concept:

• So far we discussed about matters in terms of individual atoms and molecules. Atomic mass units provide a relative scale for the masses of the elements.
• Since the atoms have such small masses, no usable scale can be devised to weigh them in the calibrated units of atomic mass units. In any real situation, we deal with macroscopic samples containing enormous number of atoms.
• Therefore, it is convenient to have a special unit to describe a very large number of atoms. The idea of a ‘unit’ to denote a particular number of objects is not new.
• For example, the pair (2 items) and the dozen (12 items), are all familiar units. Chemists measure atoms and molecules in ‘moles’. So, you can now understand that ‘mole’ denotes a number of particles.
• In the SI system, the mole (mol) is the amount of a substance that contains as many elementary entities (atoms, molecules, or other particles) as there are atoms in exactly 12 g (or 0.012 kg) of the carbon-12 isotope.
• The actual number of atoms in 12 g of carbon-12 is determined experimentally. This is called Avogadro’s Number (NA), named after an Italian scientist Amedeo Avogadro who proposed its significance.
• Its value is 6.023 × 10^23. So one mole of a substance contains 6.023 × 10^23 entities. Thus, 5 moles of oxygen molecules contain 5 × 6.023 ×10^23 molecules.

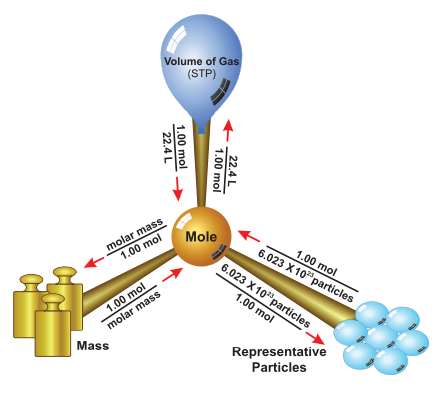
Mole Concept: The study of the collection of particles by using mole as the counting unit, in order to express the mass and volume of such unit particles in a bulk of matter is known as mole concept.

The number of moles of a substance can be calculated by various means depending on the data available, as follows:

• Number of moles of molecules.
• Number of moles of atoms.
• Number of moles of a gas (Standard molar volume at STP = 22.4 litre).
• Number of moles of ions.

Note:

STP-Standard Temperature and Pressure (273.15 K, 1.00 atm)

Mole of atoms:

• One mole of an element contains 6.023 × 10^23 atoms and it is equal to its gram atomic mass.
• i.e., one mole of oxygen contains 6.023 × 10^23 atoms of oxygen and its gram atomic mass is 16 g.

Mole of molecules:

• One mole of matter contains 6.023 × 1023 molecules and it is equal to its gram molecular mass.
• i.e., one mole of oxygen contains 6.023 × 1023 molecules of oxygen and its gram molecular mass is 32 g.

Molar volume:

One mole of any gas occupies 22.4 litre or 22400 ml at S.T.P. This volume is called as molar volume.

Calculation of number of moles by Different modes

Number of moles

= Mass / Atomic Mass

= Mass / Molecular mass

= Number of Atoms / 6.023 × 10^23

= Number of Molecules / 6.023 × 10^23

Percent Composition:

• So for, we were dealing with the number of entities present in a given substance. But many times, the information regarding the percentage of a particular element present in a compound is required.
• The percentage composition of a compound represents the mass of each element present in 100 g of the compound. Let us understand the percentage composition of oxygen and hydrogen by taking the example of H2O. It can be calculated using the formula

Mass % of an element

= mass of that element in the compound / molar mass of the compound × 100

Now,

molar mass of H2O = 2(1) + 16

= 18 g

Mass % of hydrogen = 2/18 × 100

= 11.11 %

Mass % of oxygen = 16/18 × 100

= 88.89 %

This percentage composition is useful to determine the empirical formula and molecular formula.

Example 1: Find the mass percentage composition of methane (CH4).

Molar mass of CH4 = 12 + 4 = 16 g

Mass % of carbon = 12/16× 100

= 75 %

Mass % of hydrogen = 4/16× 100

= 25 %

Avogadro Hypothesis:

• In 1811 Avogadro framed a hypothesis based on the relationship between the number of molecules present in equal volumes of gases in different conditions.
• The Avogadro’s law states that “equal volumes of all gases under similar conditions of temperature and pressure contain equal number of molecules”
• It follows that the volume of any given gas must be proportional to the number of molecules in it.
• If ‘V’ is the volume and ‘n’ is the number of molecules of a gas, then Avogadro law is represented, mathematically, as follows:

V α n

V = constant × n

Thus, one litre (1 dm3 ) of hydrogen contains the same number of molecules as in one litre of oxygen, i.e. the volume of the gas is directly proportional to the number of molecules of the gas.

Explanation:

Let us consider the reaction between hydrogen and chlorine to form hydrogen chloride gas

H2 (g) + Cl2(g) → 2 HCl (g)

1 vol + 1 vol → 2 volumes

According to Avogadro’s law 1 volume of any gas is occupied by “n” number of molecules.

n molecules + n molecules → 2n molecules

if n = 1 then

1molecule + 1 molecule → 2 molecules.

½ molecule + ½ molecule → 1 molecule

1 molecule of hydrogen chloride gas is made up of ½ molecule of hydrogen and ½ molecule of chlorine. Hence, the molecules can be subdivided. This law is in agreement with Dalton’s atomic theory.

Applications of Avogadros Law

• It explains Gay-Lussac’s law.
• It helps in the determination of atomicity of gases.
• Molecular formula of gases can be derived using Avogadro’s law
• It determines the relation between molecular mass and vapour density.
• It helps to determine gram molar volume of all gases (i.e, 22.4 litre at S.T.P)

Relationship Between Vapour Density And Relative Molecular Mass:

i. Relative molecular mass: (Hydrogen scale)

The Relative Molecular Mass of a gas or vapour is the ratio between the mass of one molecule of the gas or vapour to mass of one atom of Hydrogen.

ii. Vapour Density:

Vapour density is the ratio of the mass of a certain volume of a gas or vapour, to the mass of an equal volume of hydrogen, measured under the same conditions of temperature and pressure.

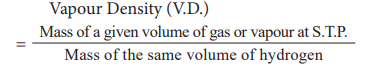
According to Avogadro’s law, equal volumes of all gases contain equal number of molecules.

Thus, let the number of molecules in one volume = n, then

Cancelling ‘n’ which is common, you get

When you compare the formula of vapour density with relative molecular mass, they can be represented as

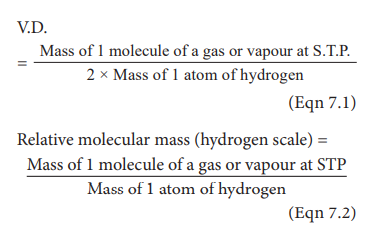
You can therefore substitute the above equation to an Eqn 7.1 and arrive at the following formula

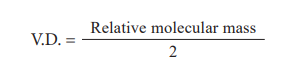
Now on cross multiplication, you have

2 × vapour density = Relative molecular mass of a gas (Or) Relative molecular mass = 2 × Vapour density

More to Know:

1. Relative Molecular Mass is only a ratio. So, it has no unit. If the molecular mass of a compound is expressed in grams, it is called Gram Molecular Mass.

• Gram Molecular Mass of water = 18 g
• Gram Molecular Mass of
• carbon dioxide = 44 g
• Gram Molecular Mass of
• ammonia = 17 g
• Gram Molecular Mass of HCl = 36.5 g

2. Relative Atomic Mass is only a ratio, so it has no unit. If the atomic mass of an element is expressed in grams, it is called as Gram Atomic Mass

• Gram Atomic Mass of hydrogen = 1 g
• Gram Atomic Mass of carbon = 12 g
• Gram Atomic Mass of nitrogen = 14 g
• Gram Atomic Mass of oxygen = 16 g

Calculation of average atomic mass – Solved Examples

Example 1: Oxygen is the most abundant element in both the Earth’s crust and the human body.

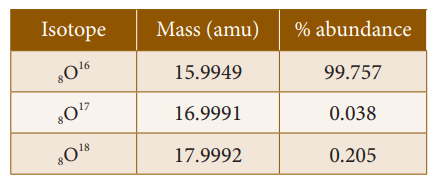
The atomic mass of

oxygen = (15.9949 × 0.99757) + (16.9991 × 0.00038) + (17.9992 × 0.00205)

= 15.999 amu.

Example 2: Boron naturally occurs as a mixture of boron-10 (5 protons + 5 neutrons) and boron-11 (5 protons + 6 neutrons) isotopes. The percentage abundance of B-10 is 20 and that of B-11 is 80. Then, the atomic mass of boron is calculated as follows:

Atomic mass of boron = (10 × 20/100) + (11 × 80/100)

= (10 × 0.20) + (11 × 0.80)

= 2 + 8.8

= 10.8 amu

Solved Problems:

I. Calculation of molar mass

Calculate the gram molar mass of the following.

1) H2O 2) CO2 3) Ca3 (PO4)2

Solution:

1) H2O

Atomic masses of H = 1, O = 16

Gram molar mass of H2O

= (1 × 2) + (16 × 1)

= 2 + 16

Gram molar mass of H2O = 18 g

2) CO2

Atomic masses of C = 12, O = 16

Gram molar mass of CO2

= (12 × 1) + (16 × 2)

= 12 + 32

Gram molar mass of CO2 = 44 g

3) Ca3 (PO4)2

Atomic masses of Ca = 40, P = 30, O = 16.

Gram molar mass of Ca3 (PO4)2

= (40 × 3) + [30 + (16 × 4)] × 2

= 120 + (94 × 2)

= 120 + 188

Gram molar mass of Ca3 (PO4)2 = 308 g

II. Calculation based on number of moles from mass and volume

1) Calculate the number of moles in 46 g of sodium?

Number of moles = Mass of the element/Atomic mass of the element

= 46 / 23

= 2 moles of sodium

2) 5.6 litre of oxygen at S.T.P

Number moles =Given volume of O2 at S.T.P /Molar volume at S.T.P

Number of moles of oxygen = 5.6/22.4

= 0.25 mole of oxygen

3) Calculate the number of moles of a sample that contains 12.046 × 1023 atoms of iron?

Number of moles = Number of atoms of iron/Avogadro’s number

= 12.046 × 10^23 / 6.023 × 10^23

= 2 moles of iron

III. Calculation of mass from mole

Calculate the mass of the following

1) 0.3 mole of aluminium (Atomic mass of Al = 27)

Number of moles = Mass of Al/Atomic mass of Al

Mass = No. of moles × atomic mass

So, mass of Al = 0.3 × 27

= 8.1 g

2) 2.24 litre of SO2 gas at S.T.P

Molecular mass of SO2 = 32 + (16 × 2)

= 32 + 32 = 64

Number of moles of SO2 = Given volume of SO2 at S.T.P/Molar volume SO2 at S.T.P

Number of moles of SO2 = 2.24/22.4

= 0.1 mole

Number of moles = Mass/Molecular mass

Mass = No. of moles × molecular mass

Mass = 0.1 × 64

Mass of SO2 = 6.4 g

3) 1.51 × 10^23 molecules of water

Molecular mass of H2O = 18

Number of moles =Number of molecules of water/Avogadro’s number

= 1.51 × 10^23 / 6.023 × 10^23

= 1 / 4

= 0.25 mole

Number of moles = Mass/Molecular mass

0.25 = mass / 18

Mass = 0.25 × 18

Mass = 4.5 g

4) 5 × 10^23 molecules of glucose ?

Molecular mass of glucose = 180

Mass of glucose = (Molecular mass ×number of particles)/Avogadro’s number

= (180 × 5 × 1023) / 6.023 × 1023

= 149.43 g

IV. Calculation based on number of atoms/molecules.

1) Calculate the number of molecules in 11.2 litre of CO2 at S.T.P

Number of moles of CO2 = Volume at S.T.P/Molar volume

= 11.2 / 22.4

= 0.5 mole

Number of molecules of CO2 = number of moles of CO2 × Avogadro’s number

= 0.5 × 6.023 × 102^3

= 3.011 × 10^23 molecules of CO2

2) Calculate the number of atoms present in 1 gram of gold (Atomic mass of Au = 198)

Number of atoms of Au = Mass of Au × Avogadro’s number/Atomic mass of Au

Number of atoms of Au = 1/198× 6.023 × 10^23

Number of atoms of Au = 3.042 × 10^21 g

3) Calculate the number of molecules in 54 gm of H2O?

Number of molecules = (Avogadro number× Given mass)/Gram molecular mass

Number of molecules of water = 6.023 × 10^23 × 54 / 18

= 18.069 × 10^23 molecules

4) Calculate the number of atoms of oxygen and carbon in 5 moles of CO2.

• 1 mole of CO2 contains 2 moles of oxygen
• 5 moles of CO2 contain 10 moles of oxygen

Number of atoms of oxygen = Number of moles of oxygen × Avogadro’s number

= 10 × 6.023 × 10^23

= 6.023 × 1024 atoms of Oxygen

• 1 mole of CO2 contains 1 mole of carbon
• 5 moles of CO2 contains 5 moles of carbon

No. of atoms of carbon = No. of moles of carbon × Avogadro’s number

= 5 × 6.023 × 10^23

= 3.011 × 1024 atoms of Carbon

V. Calculation based on molar volume

Calculate the volume occupied by:

1) 2.5 mole of CO2 at S.T.P

Number of moles of CO2 = Given volume at S.T.P/Molar volume at S.T.P

2.5 mole of CO2 = Volume of CO2 at S.T.P/22.4

Volume of CO2 at S.T.P = 22.4 × 2.5

= 56 litres.

2) 3.011 × 10^23 of ammonia gas molecules

Number of moles = Number of molecules/Avogadro’s number

= 3.011 × 1023 / 6.023 × 1023

= 2 moles

Volume occupied by NH3

= number of moles × molar volume

= 2 × 22.4

= 44.8 litres at S.T.P

3) 14 g nitrogen gas

Number of moles = 14 / 28

= 0.5 mole

Volume occupied by N2 at S.T.P

= no. of moles × molar volume

= 0.5 × 22.4

= 11.2 litres.

VI. Calculation based on % composition

Calculate % of S in H2SO4

Molar mass of H2SO4

= (1 × 2) + (32 × 1) + (16 × 4)

= 2 + 32 + 64

= 98 g

% of S in H2SO4 = (Mass of sulphur /Molar mass of H2SO4) * 100

% of S in H2SO4 = 32/98× 100

= 32.65