விசையும் இயக்கமும் Notes 7th Science Lesson 2 Notes in Tamil

7th Science Lesson 2 Notes in Tamil

2] விசையும் இயக்கமும்

அறிமுகம்:

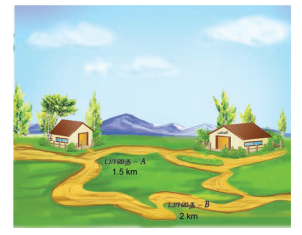
மேலே கொடுக்கப்பட்டிருக்கும் படத்தில் காட்டியபடி கவிதா தனது வீட்டிலிருந்து இரு வழிகளில் பள்ளிக்கு செல்ல முடியும். எப்பாதையின் வழியாகச் சென்றால் அவளால் விரைவில் பள்ளியை அடைய இயலும் என உங்களால் கூற இயலுமா?

பாதை – A

பாதை – B

அருகில் உள்ள படத்தினைப் பாருங்கள்.

எந்தப் பாதையின் வழியாக இலை கீழே விழும்போது தரையை வேகமாக வந்தடையும்?

உமாவும், பிரியாவும் ஒரே பள்ளியில் படிக்கும் தோழிகள். அவர்கள் இருவரும் பள்ளி நேரம் முடிந்தவுடன் அருகில் உள்ள விளையாட்டுத் திடலுக்குச் சென்று விளையாடி விட்டு வீடு திரும்புவார்கள். ஒரு நாள் உமா தனது பாட்டி வீட்டிற்குச் சென்றுவிட்டுத் திடலுக்கு வருவதாகக் கூறிச்சென்றாள். இருவரும் விளையாட்டுத்திடலுக்குச் சென்ற பாதை படத்தில் காட்டப்பட்டுள்ளது.

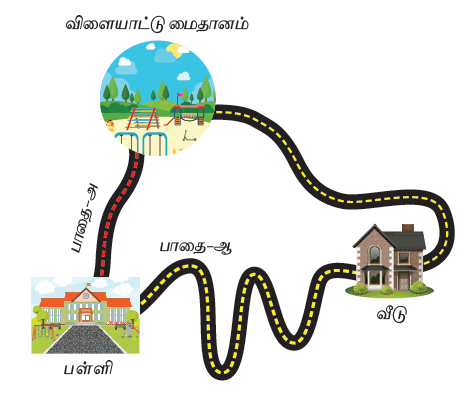
ஒரு நூலினை எடுத்துக் கொள்ளுங்கள். அதனை பயன்படுத்தி, படத்தில் காட்டியுள்ள பாதையின் (அ மற்றும் ஆ) நீளங்களை அளந்து கொள்ளுங்கள். எப்பதையின் நீளம் அதிகமாக உள்ளது எனக் கூறுங்கள்.

மேற்கண்ட நிகழ்வுகளில் இருந்து ஒரு பொருளானது ஓர் இடத்திலிருந்து மற்றோர் இடத்திற்குச் செல்லும்போது அவ்விரு இடங்களையும் இணைக்கும் நேர்க்கோட்டு பாதையில் சென்றால் மற்ற பாதைகளில் செல்வதனைக் காட்டிலும் விரைவில் அவ்விடத்தினைச் சென்று அடையலாம் என நாம் அறிகிறோம். இரு புள்ளிகளுக்கு இடையேலான நேர்கோட்டுப்பாதையில் மிகக் குறைந்த தொலைவு அமைகிறது.

தொலைவு மற்றும் இடப்பெயர்ச்சி தொலைவு:

ஓர் இடத்திலிருந்து மற்றோர் இடத்திற்கு, ஒரு பொருள் கடந்து வந்த பாதையின் மொத்த நீளம் தொலைவு எனப்படும்.

இடப்பெயர்ச்சி:

ஒரு பொருளின் இயக்கத்தின்போது, அதன் துவக்க நிலைக்கும் இறுதி நிலைக்கும் இடையே உள்ள மிகக் குறைந்த நேர்க்கோட்டுத் தொலைவு இடப்பெயர்ச்சி எனப்படும்.

தொலைவு மற்றும் இடப்பெயர்ச்சி இவை இரண்டும் ஒரே அலகால் குறிக்கப்படுகின்றன. இவற்றின் SI அலகு மீட்டர் (மீ) ஆகும்.

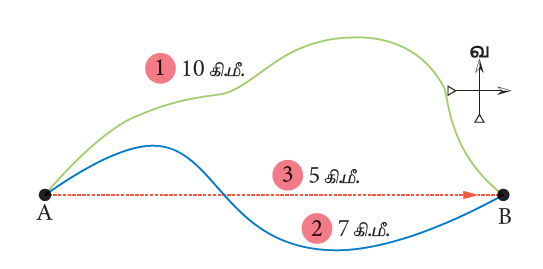
ஒருவர் படத்தில் காட்டியவாறு A என்ற இடத்திலிருந்து B என்ற இடத்திற்குப் பயணம் செய்கிறார் எனக்கொள்வோம்.

இதில் முதல் பாதையின் வழியாகச் செல்லும்போது அவர் 10 கி.மீ தூரம் பயணத்தினை மேற்கொள்கிறார். இரண்டாவது பாதையின் வழியாகப் பயணம் செய்யும்போது 7 கி.மீ தூரம் பயணம் செய்கிறார்.

முதல் பாதையில் அவர் கடந்த தொலைவு 10 கி.மீ.

இரண்டாவது பாதையில் அவர் கடந்த தொலைவு 7 கி.மீ.

A மற்றும் Bக்கு இடையே உள்ள நேர்க்கோட்டு தொலைவு ஆனது இடப்பெயர்ச்சி 5 கி.மீ (3 எனக்குறிக்கப்பிட்டுள்ளது).

எனவே, எந்த பாதையில் அவர் பயணம் செய்தாலும் அவரது இடப்பெயர்ச்சி 5 கி.மீ (கிழக்கு திசையில்) ஆகும்.

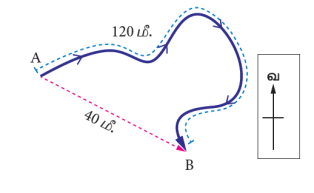
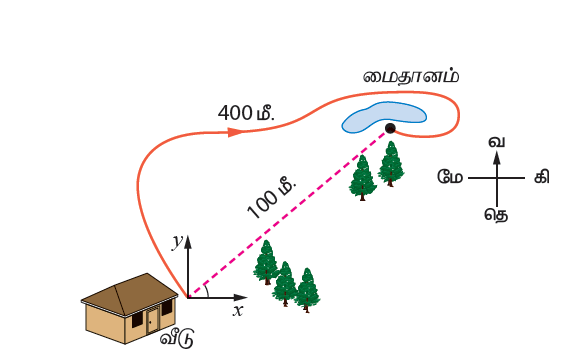
Aயிலிருந்து Bக்கு பயணம் செய்யும் ஒரு பொருளின் பாதையானது படத்தில் காட்டப்பட்டுள்ளது. பொருளானது பயணம் செய்த மொத்த தொலைவு 120 மீ. பொருளின் இடப்பெயர்ச்சி 40 மீ (தென்கிழக்கு திசையில்).

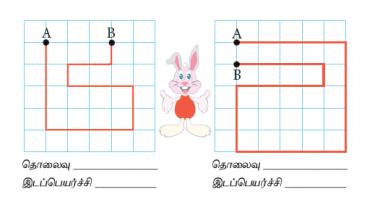
முயல் ஒன்று ஓடிய பாதை படத்தில் காட்டப்பட்டுள்ளது. ஒவ்வொரு படத்திலும் அது கடந்த தொலைவையும் இடப்பெயர்ச்சியையும் கண்டறிக. ஓவ்வொரு சிறிய கட்டத்தின் பக்க அளவு ஒரு மீட்டர் என்ற அளவில் உள்ளதாகக் கொள்க. முயல் A என்ற புள்ளியில் ஓடத்துவங்கி B என்ற புள்ளியை வந்தடைகிறது.

• எப்பொழுது முயல்/மொத்த கடந்த தொலைவும், அதன் இடப்பெயர்ச்சியும் சமமாக இருக்கும் என விளக்குக. ஆனால் முயல் ஓடத்துவங்கிய புள்ளியும், முடித்தப் புள்ளியும் வெவ்வேறாக இருக்க வேண்டும்.

நாம் ஒரு பொருளின் இடப்பெயர்ச்சியை குறிப்பிடும்போது அது பயணம் மேற்கொள்ளும் திசையைப் பொறுத்து நேர்குறி அல்லது எதிர்குறியைப் பயன்படுத்துகிறோம்.

இங்கு பொருளின் ஆரம்பு நிலையை A எனக்கொண்டு பொருள் Aயிலிருந்து Bக்கு செல்லும் போது நேர்குறியையும், Bயிலிருந்து Aக்கு செல்லும்போது எதிர்குறியையும் பயன்படுத்துகிறோம்.

வேகம் – திசைவேகம்:

வேகம்:

மீள் பார்வை:

நாம் வேகம் என்பதனைப் பற்றி ஆறாம் வகுப்பில் படித்துள்ளோம்.

தொலைவு மாறுபடும் வீதம் வேகம் எனப்படும்.

வேகம் = தொலைவு/காலம்.

இதன் அலகு மீட்டர்/விநாடி (மீ/வி)

வேகத்தினை நாம் சீரான வேகம் மற்றும் சீரற்ற வேகம் என இரு வகைகளாகப் பிரிக்கலாம்.

சீரான வேகம்:

ஒரு பொருள் சமகால இடைவெளிகளில் சம தொலைவினைக் கடந்தால் அப்பொருள் சீரான வேகத்தில் செல்கிறது எனப்படும்.

சீரற்ற வேகம்:

ஒரு பொருள் வெவ்வேறு கால இடைவெளிகளில் வெவ்வேறு தொலைவினைக் கடந்தால் அப்பொருள் சீருற்ற வேகத்தில் செல்கிறது எனப்படும்.

சராசரி வேகம் = கடந்த மொத்தத் தொலைவு/எடுத்துக்கொண்ட மொத்தக் காலம்.

திசைவேகம்:

இடப்பெயர்ச்சி மாறுபடும் வீதம் திசைவேகம் எனப்படும்.

திசைவேகம் (V) = இடப்பெயர்ச்சி/காலம்

திசைவேகத்தின் SI அலகு மீட்டர்/விநாடி (மீ/வி) ஆகும்.

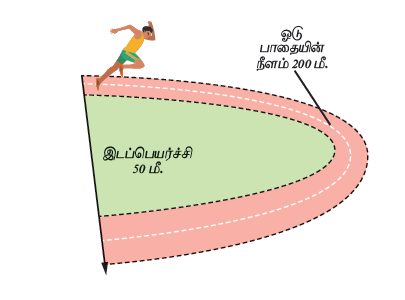
• படத்தில் காட்டியவாறு ஒரு விளையாட்டு வீராங்கனை 25 விநாடியில் 200 மீட்டர் ஓட்டத்தினை நிறைவு செய்தார் என்றால் அவரின் வேகம் மற்றும் திசைவேகத்தினைக் காண்க.

வேகம் = கடந்த தொலைவு/காலம்

= 200/25

= 8 மீ/வி

திசைவேகம் = இடப்பெயர்ச்சி /காலம்

= 50/25

= 2 மீ/வி

சீரான திசைவேகம்:

ஒரு பொருளானது தன் இயக்கத்தின் போது தனது திசையினை மாற்றாமல் சீரான கால இடைவெளியில் சீரான இடப்பெயர்ச்சியினை மேற்கொண்டால் அது சீரான திசைவேகத்தில் இயங்குகிறது எனப்படும். (எ.கா) வெற்றிடத்தில் பயணம் செய்யும் ஒளி.

சீரற்ற திசைவேகம்:

ஒரு பொருளானது தனது திசையையோ அல்லது வேகத்தினையே மாற்றிக்கொண்டால் அப்பொருள் சீரற்ற திசைவேகத்தில் உள்ளது எனப்படும். (எ.கா)இரயில் நிலையத்திற்கு வரும் தொடர்வண்டியின் இயக்கம்.

சராசரி திசைவேகம்:

சராசரி திசைவேகம் = மொத்த இடப்பெயர்ச்சி/எடுத்துக்கொண்ட காலம்

(எ.கா) படத்தில் காட்டியுள்ளவாறு ஒரு மகிழுந்தானது கிழக்கு திசையில் 5 கி.மீ தூரம் பயணம் செய்கிறது. பின்னர் திரும்பி அதே பாதையில் மேற்கு நோக்கி 7 கி.மீ தூரம் பயணம் செய்கிறது. இப்பயணத்தினை நிறைவு செய்ய அது 0.2 மணி நேரம் எடுத்துக்கொள்கிறது எனில் அதன் சராசரி திசைவேகத்தினைக் காண்க.

சராசரி திசைவேகம் = மொத்த இடப்பெயர்ச்சி/காலம்

= 7 – 50/2

= 2/0.2

= 10 கி.மீ/மணி (அ) 10 x 5/18 = 25/9 = 0.28 மீ/வி.

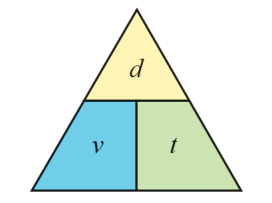
மேலே காணப்படும் முக்கோணமானது முறையானது திசைவேகம் (V), இடப்பெயர்ச்சி (d) மற்றும் காலம் (t) இவற்றுக்கிடையே உள்ள தொடர்பினை எளிதாகப் புரிந்துக்கொள்ள உதவுகிறது.

v = d/t, t = d/v, d= v x t = கட்டம்

விடையளி:

• சீரான திசைவேகத்தில் தெற்கு நோக்கி 100 மீ தொலைவினை 4 விநாடிகளில் கடக்கும் மகிழுந்தின் திசைவேகத்தைக் கண்டறிக.
• உசைன் போல்ட் 100 மீ தூரத்தினை 9.58 விநாடிகளில் கடந்தார். அவரது வேகத்தினைக் கண்டறிக. 30 மீ/வி வேகத்தில் ஓடக்கூடிய சிறுத்தையுடன், உசைன் போல்ட் ஓட்டப்பந்தயத்தில் கலந்து கொண்டால் வெற்றி யாருக்கு?
• நீங்கள் 4 மீ கிழக்கு நோக்கி நேராக நடந்து, பின்னர் 2 மீ தெற்கு நோக்கியும், அடுத்து 4 மீ மேற்கு நோக்கியும், கடைசியாக 2 மீ வடக்கு நோக்கியும் நடக்கிறாய். நீங்கள் மொத்த தூரத்தினை 24 விநாடிகளில் கடக்கிறாய்.

உனது சராசரி வேகம் எவ்வளவு? சுராசரி திசைவேகம் எவ்வளவு?

முடுக்கம் (a) :

திசைவேகம் மாறும் வீதம் முடுக்கம் எனப்படும். வேறு வகையில் கூறுவதனால், ஒரு பொருளின் வேகத்திலோ அல்லது திசையிலோ மாற்றம் ஏற்பட்டால் அப்பொருள் முடுக்கமடைகிறது எனப்படும்.

முடுக்கம் (a) = திசைவேக மாற்றம்/காலம்

= இறுதித் திசைவேகம் (v) – ஆரம்பத் திசைவேகம் (u) / காலம் (t)

a = (v-u)/t

முடுக்கத்தின் SI அலகு மீ/வி²

ஒரு பொருளின் வேகத்திலோ அல்லது திசையிலோ அல்லது வேகம் மற்றும் திசை இவை இரண்டிலும் மாற்றம் ஏற்பட்டால் அப்பொருளானது முடுக்கமடைகிறது எனப்படும்.

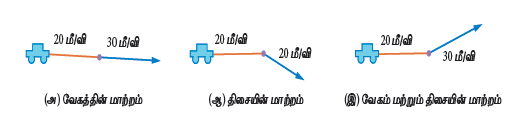
ஒரு தொடர்வண்டி நேர்கோட்டில் பயணம் செய்யும் பாதையைக் கீழே உள்ள படமானது காட்டுகிறது. படத்தினைப் பார்த்து அட்டவணையைப் பூர்த்தி செய்யவும்.

விடையளி:

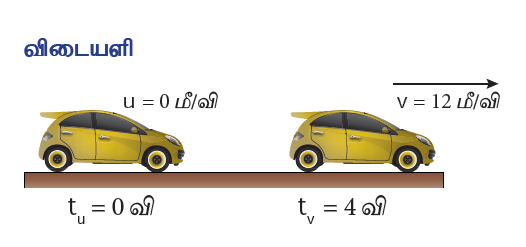
ஓய்வு நிலையில் உள்ள ஒரு மகிழுந்தானது, நேர்க்ககோட்டில் இயங்கத் தொடங்குகிறது எனக் கொள்க. அது 4 விநாடிகளில் 12 மீ/வி வேகத்தினை அடைகிறது எனில் அதன் முடுக்கத்தினைக் கணக்கிடுக. மகிழுந்து சீராக முடுக்கத்தில் உள்ளது எனக் கொள்க.

ஆரம்பத் திசைவேகம் (u) = 0 மீ/வி

இறுதி திசைவேகம் (v) = 12 மீ/வி

எடுத்துக்கொண்ட நேரம் (t) = 4 வி

முடுக்கம் a = (v-u)/t

= (12 – 0)/4

= 3 மீ/வி²

விடையளி:

மேற்கண்ட தகவலில் இருந்து சிறுத்தையின் முடுக்கத்தினை உன்னால் கணக்கிட்டுக் கூற முடியுமா?

நேர்முடுக்கம்:

ஒரு பொருளின் திசைவேகமானது காலத்தினைப் பொருத்து அதிகரித்துக் கொண்டே வந்தால் அப்பொருளில் ஏற்படும் முடுக்கம் நேர் முடுக்கம் எனப்படும்.

எதிர் முடுக்கம்:

ஒரு பொருளின் திசைவேகமானது காலத்தினைப் பொருத்து குறைந்து கொண்டே வந்தால் அப்பொருளில் ஏற்படும் முடுக்கம் எதிர்முடுக்கம் எனப்படும்.

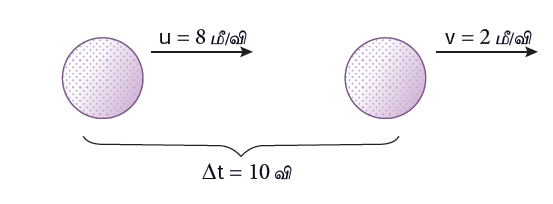
• ஒரு நேர்கோட்டு பாதையில் 8 மீ/வி என்ற திசைவேகத்தில் இயங்கிக் கொண்டிருக்கும் பந்தானது 10 விநாடியில் 2 மீ/வி என்ற திசைவேகத்தினை அடைகிறது. அப்பொருள் பெறும் எதிர்முடுக்கம் யாது?

ஆரம்ப திசைவேகம் (u) = 8 மீ/வி

இறுதி திசைவேகம் (v) = 2 மீவி

எடுத்துக்கொண்ட நேரம் (t) = 10 வி

முடுக்கம் (a) = (v – u)/t

= (2 – 8)/10

= -0.6 மீ/வி²

சீரான முடுக்கம்:

ஒரு பொருளில் சீரான கால இடைவெளியில் காலத்தினைப் பொருத்து திசைவேகத்தில் ஏற்படும் மாற்றம் (அதிகரித்தல் அல்லது குறைதல்) சீரானதாக இருப்பின் அம்முடுக்கம் சீரான முடுக்கம் எனப்படும்.

காலத்தைப் பொருத்து ஒரு பேருந்தின் திசைவேகமானது அட்டவணையில் கொடுக்கப்பட்டுள்ளது.

நேரம் வி	1	2	3	4	5
திசைவேகம் (மீ/வி)	20 + 20	40 + 20	60 + 20	80 + 20	100 + 20
(நேர் முடுக்கம்)
	100 – 20	80 – 20	60 – 20	40 – 20	20 – 20
(எதிர் முடுக்கம்)

இங்கு பொருளின் திசைவேகமானது 20 மீ/வி என்ற நேரத்தில் மாற்றம் அடைவதால் (அதிகரித்தல் அல்லது குறைதல்) இதன் முடுக்க மாற்றம் 20 மீட்டர்/வி² ஆகும்.

சீரற்ற முடுக்கம்:

ஒரு பொருளின் திசைவேகத்தில் காலத்தைப் பொருத்து ஏற்படும் மாற்றமானது சீரற்றதாக இருந்தால் அம்முடுக்கமானது சீரற்ற முடுக்கம் எனப்படும்.

நேரம் (வி)	0	1	2	3	4	5
திசைவேகம் (மீ/வி)	0	10	40	60	70	50
திசை வேகமாற்றம்	0	10	30	20	10	20

இங்கு ஒவ்வொறு விநாடிக்கும் திசைவேகத்தில் ஏற்படும் மாற்றம் மாறுபடுவதைக் காணலாம். எனவே இம்முடுக்கம் சீரற்ற முடுக்கம் எனப்படும்.

தொலைவு – காலம் வரைபடங்கள்

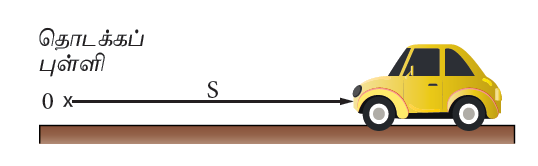
ஒரு மகிழுந்தானது O என்ற புள்ளியில் இருந்து புறப்பட்டுச் செல்வதாகக் கருதுவோம். ஓவ்வொரு விநாடி நேரத்திற்கும் அது கடக்கும் தொலைவானது அளக்கப்படுகிறது. தொலைவு மற்றும் காலம் பதிவு செய்யப்பட்டு அதற்கான வரைபடமானது வரையப்படுகிறது. இந்நிகழ்வில் காணப்படும் நான்கு சாத்தியக்கூறுகள் கீழே கொடுக்கப்பட்டுள்ளன.

மகிழுந்து ஓய்வுநிலையில் இருந்தல்:

காலம் (வி)	0	1	2	3	4	5
தொலைவு (மீ)	0	20	20	20	20	20

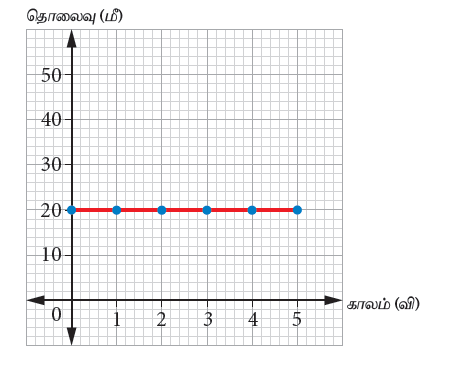
இந்த வரைபடத்தில், நேர்கோட்டின் சாய்வு சுழி மதிப்பினைப் பெற்றுள்ளது. அதாவது ஒவ்வொரு விநாடி காலத்திற்கும் தொலைவானது மாறாமல் உள்ளது. மகிழுந்து ஓய்வு நிலையில் உள்ளது.

ஆ) மகிழுந்து 10 மீ/வி என்ற சீரான வேகத்தில் செல்லுதல்

காலம் (வி)	0	1	2	3	4	5
தொலைவு (மீ)	0	10	20	30	40	50

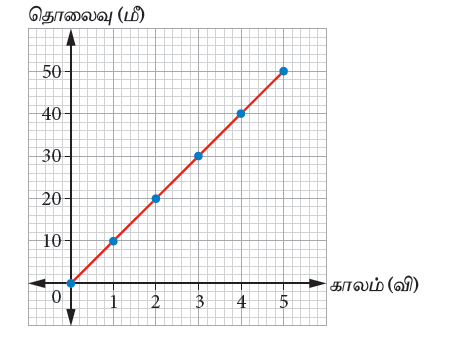
வரைபடத்தில் சாய்வானது மாறா மதிப்பினைப் பெற்றுள்ளது. இதன் தொலைவானது ஒவ்வொரு விநாடி காலத்திற்கும் 10 மீட்டர் அளவில் உள்ளது. எனவே மகிழுந்து சீரான வேகத்தில் செல்கிறது.

இ) மகிழுந்தின் வேகம் அதிகரித்துக் கொண்டே செல்லுதல்:

காலம் (வி)	0	1	2	3	4	5
தொலைவு (மீ)	0	5	20	45	80	125

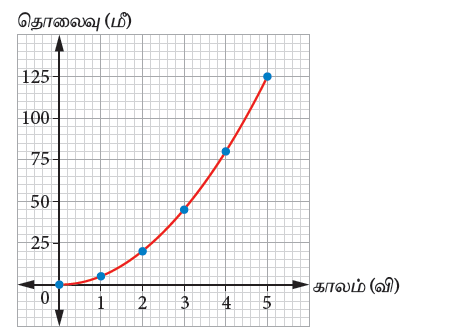
வரைபடத்தில், ஒவ்வொரு குறிப்பிட்ட கால இடைவெளியிலும் (1 விநாடி), மகிழுந்து கடக்கும் தூரம் அதிகரிக்கிறது.

எனவே, மகிழுந்தின் வேகம் அதிகரித்துக் கொண்டே செல்கிறது. இதனை, வளை வரையின் சாய்வின் மதிப்பு அதிகரித்துக் கொண்டேச் செல்வதன் மூலம் அறியலாம்.

ஈ) மகிழுந்தின் வேகம் குறைந்துக் கொண்டே செல்லுதல்:

காலம் (வி)	0	1	2	3	4	5
தொலைவு (மீ)	0	45	80	105	120	125

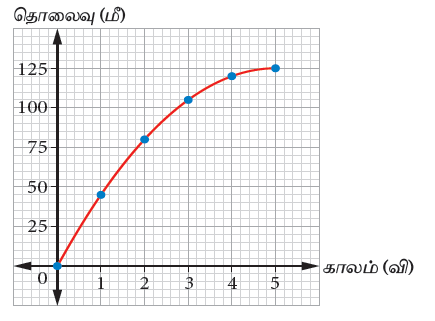
வரைபடத்தில், ஒவ்வொரு குறிப்பிட்ட கால இடைவெளியிலும் (1 விநாடி), மகிழுந்து கடக்கும் தூரம் குறைகிறது.

எனவே, மகிழுந்தின் வேகம் குறைந்துக் கொண்டே செல்கிறது. இதனை, வளைவரையின் சாய்வின் மதிப்பு குறைந்துக் கொண்டேச் செல்வதன் மூலம் அறியலாம்.

வேகம் – காலம் வரைபடம்:

ஒரு பேருந்தானது தஞ்சையிலிருந்து திருச்சியை நோக்கிச் செல்வதாகக் கருதுவோம். ஓவ்வொரு விநாடிக்கும் அதன் வேகமானது கணக்கிடப்படுகிறது. இதன் வேகம் மற்றும் காலத்தின் மதிப்புகள் அட்டவணைப்படுத்தப்பட்டு வரைபடமானது வரையப்படுகிறது. இவ்வரைபடம் வேகம் – காலம் வரைபடம் எனப்படுகிறது. இந்நிகழ்வில் காணப்படும் சாத்தியக்கூறுகள் கீழே கொடுக்கப்பட்டுள்ளன.

1. பேருந்து ஓய்வு நிலையில் இருத்தல்:

காலம் (வி)	0	1	2	3	4	5
வேகம் (மீ/ வி)	0	0	0	0	0	0

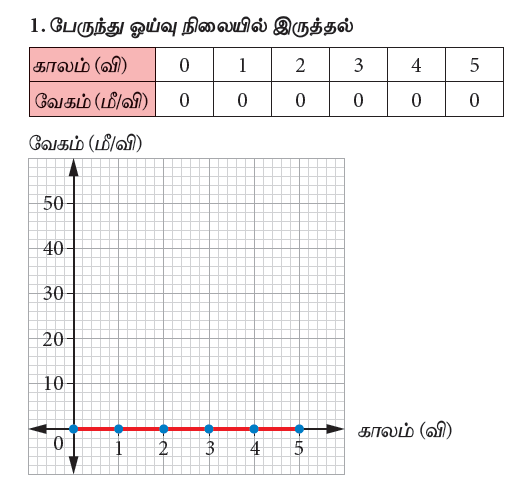
இதன் வேகம் 0 மீ/வி என்ற நிலையிலேயே உள்ளது. எனவே பேருந்து சுழி முடுக்கத்தினைக் கொண்டுள்ளது.

2. பேருந்து சீரான வேகத்தில் செல்லுதல்:

காலம் (வி)	0	1	2	3	4	5
வேகம் (மீ/ வி)	10	10	10	10	10	10

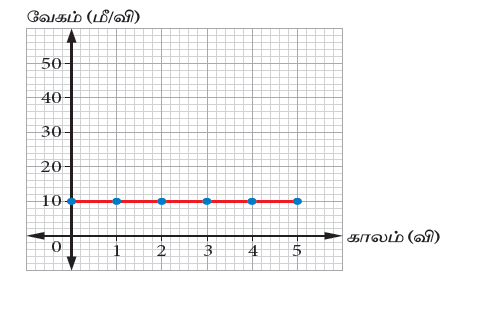
பேருந்தானது 10 மீ/வி என்ற மாறாத வேகத்தில் சென்று கொண்டிருக்கிறது. வரைபடத்தில், நேர்கோட்டின் சாய்வு சுழி மதிப்பைக் கொண்டுள்ளது. எனவே இதன் முடுக்கம் சுழியாகும்.

3. பேருந்து சீரான முடுக்கத்தில் செல்லுதல்:

காலம் (வி)	0	1	2	3	4	5
வேகம் (மீ/ வி)	10	10	20	30	40	50

பேருந்தானது ஒவ்வொரு விநாடிக்கும் 10 மீ/வி என்ற அதிகரிக்கும் வேகத்தில் சென்று கொண்டிருக்கிறது. வரைபடத்தில் நேர்கோட்டின் சாய்வானது நேர்குறியுடன் மாறாத மதிப்பைக் கொண்டுள்ளது. எனவே இதன் முடுக்கம் மாறிலியாகும்.

4. பேருந்து சீரான எதிர் முடுக்கத்தில் செல்லுதல்:

காலம் (வி)	0	1	2	3	4	5
வேகம் (மீ/ வி)	50	40	30	20	10	0

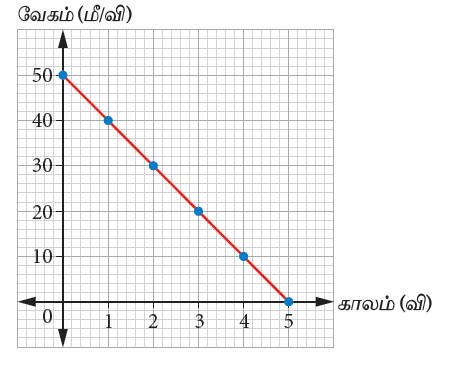
பேருந்தானது ஒவ்வொரு விநாடிக்கும் 10 மீ/வி என்ற வேகத்தில் குறைந்து கொண்டு செல்கிறது. வரைபடத்தில், நேர்கோட்டின் சாய்வானது எதிர்குறி மாறாத மதிப்பைக் கொண்டுள்ளது. எனவே இதன் முடுக்கம் மாறிலியாகும். முடுக்கமானது எதிர் முடுக்கம் என அழைக்கப்படுகிறது.

5. பேருந்தின் முடுக்கம் அதிகரித்தல் (சீரற்ற முடுக்கம்):

காலம் (வி)	0	1	2	3	4	5
வேகம் (மீ/ வி)	0	2	8	18	32	50

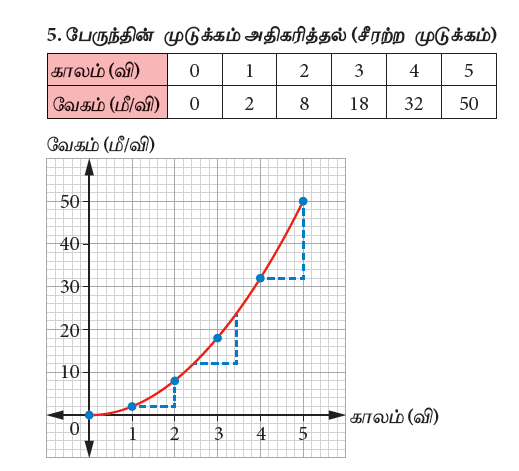
பேருந்தின் வேகமானது ஒவ்வொரு விநாடிக்கும் அதிகரித்துக் கொண்டு செல்கிறது. வரைபடத்தில், வளைவரையின் சாய்வானது நேர்குறி மதிப்பைக் கொண்டு அதிகரித்துக் கொண்டே செல்கிறது. எனவே, இதன் முடுக்கம் அதிகரிக்கிறது.

6. பேருந்தின் முடுக்கம் குறைதல் (சீரற்ற முடுக்கம்):

காலம் (வி)	0	1	2	3	4	5
வேகம் (மீ/ வி)	0	18	32	42	48	50

பேருந்தின் வேகமானது காலத்தினைப் பொருத்து சீரற்ற முறையில் குறைந்து கொண்டு செல்வதாகக் கருதுவோம். வரைபடத்தில், வளைவரையின் சாய்வானது நேர்குறி மதிப்பைக் கொண்டு குறைந்து கொண்டு செல்கிறது. எனவே இதன் முடுக்கத்தின் மதிப்பும் குறைந்து கொண்டு செல்கிறது.

ஓப்பீடு – தொலைவு – காலம் வரைபடம் மற்றும் வேகம் – காலம் வரைபடம்:

தொலைவு – காலம் வரைபடமும் வேகம் – காலம் வரைபடமும் ஒன்றுபோல் காணபட்டாலும் அவை நமக்குப் பொருளின் பயணம் பற்றிய வேவ்வேறு தகவல்களை அளிக்கின்றன. தொலைவினையும் வேகத்தினையும் y அச்சில் பிரதியிட்டு இதனை ஒப்பீடு செய்து காண்போம்.

ஒரு பேருந்தானது A என்ற இடத்திலிருந்து D என்ற இடத்தினை நோக்கிச் செய்த பயணமானது கீழே கொடுக்கப்பட்டுள்ளது.

Aயிலிருந்து B வரை பேருந்தானது அமைதி நிலையில் இருந்து முடுக்கம் அடைகிறது.

Bயிலிருந்து C வரை பேருந்தானது மாறாத திசைவேகத்துடன் பயணம் செய்கிறது.

Cயிலிருந்து D வரை பேருந்தின் முடுக்கமானது குறைந்து கொண்டே வந்து ஓய்வு நிலையை நோக்கி செல்கிறது.

தொலைவு – காலம் வரைபடம்:

தொலைவு (மீட்டர்)

தொலைவானது காலத்தினைப் பொருத்து அதிகரிக்கிறது. இது அதிகரிப்பு அளவும் அதிகரித்துக் கொண்டு செல்கிறது. எனவே இதன் சாய்வானது அதிகரிக்கிறது. இது குழிந்த கோட்டினால் குறிக்கப்படுகிறது.

தொலைவானது காலத்தினைப் பொருத்து சீராக அதிகரித்துக் கொண்டு செல்கிறது. எனவே இதன் சாய்வானது நேர்குறி மாறாத பெறுகிறது. இது நேர்க்கோட்டினால் குறிக்ப்படுகிறது.

தொலைவானது அதிகரித்துக் கொண்டு செல்கிறது. ஆனால் காலத்தினைப் பொருத்து அதிகரிக்கும் அளவானது குறைந்து கொண்டு செல்கிறது. (இது குவிந்த கோட்டினால் குறிக்கப்படுகிறது).

வேகம் – காலம் வரைபடம்:

வேகம் (மீ/வி)

வேகமானது காலத்தினைப் பொருத்து சீராக அதிகரித்துக் கொண்டு செல்கிறது. எனவே இதன் சாய்வானது நேர்குறி மாறாத மதிப்பைக் கொண்டுள்ளது. இது நேர்க்கோட்டினால் குறிக்கப்படும்.

வேகம் மாறிலியாக உள்ளது. எனவே வரைபடத்தின் கோடானது படுக்கைகோடாக உள்ளது.

வேகமானது சீராகக் குறைந்து கொண்டு வருகிறது. எனவே இதன் சாய்வானது எதிர்குறி மதிப்பைக் கொண்டுள்ளது. வரைபடமானது நேர்க்கோட்டினால் குறிக்கப்படுகிறது.

ஈர்ப்பு மையம் மற்றும் சமநிலை:

ஈர்ப்பு மையம்:

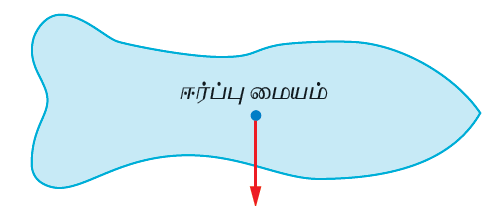
புவியின் ஈர்ப்பு (எடை) விசை, பொருளின் ஈர்ப்பு மையம் வழியேசி செயல்படுகிறது.

ஓர் அட்டையினை உங்களது விரல் நுனியில் நிலையாக நிறுத்துவதற்கு முயற்சி செய்யவும்.

இம்முயற்சியில் நீங்கள் என்ன உணர்கிறீர்கள்? ஓர் இடத்தில் மட்டுமே அட்டையானது நிலையாக நிற்கிறது என்பதனையும் வேறு எந்த இடத்திலும் அட்டையினை நிறுத்துவதற்கு முயற்சி செய்யும்போதும் அட்டையாது நிலையாக நிற்கவில்லை என்பதனையும் உணர்கிறோம். அட்டையானது எந்த இடத்தில் நிலையாக நிற்கிறதோ அப்புள்ளியினை நாம் அட்டையின் ஈர்ப்பு மையம் என்கிறோம்.

ஈர்ப்பு மையம் – எப்புள்ளியில் ஒரு பொருளின் எடை முழுவதும் செயல்படுவது போல் தோன்றுகிறதோ அப்புள்ளியே அப்பொருளின் ஈர்ப்பு மையம் எனப்படும்.

ஒரு பொருளின் ஈர்ப்பு மையத்தினை நாம் எவ்வாறு காணலாம்?

ஒழுங்கான வடிவம் கொண்ட பொருள்களின் ஈர்ப்பு மையம்

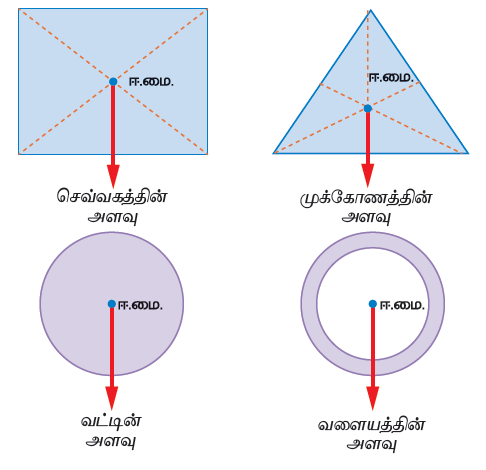
ஒழுங்கான வடிவம் கொண்ட பொருள்களின் ஈர்ப்பு மையமானது பொதுவாக அதன் வடிவியல் மையத்தில் அமைகிறது.

சில ஒழுங்கான வடிவம் கொண்ட பொருள்களின் ஈர்ப்பு மையமானது கீழே கொடுக்கப்பட்டுள்ளது.

ஒழுங்கற்ற வடிவம் கொண்ட பொருள்களின் ஈர்ப்பு மையத்தினை எவ்வாறு காணலாம்?

தேவையான பொருள்கள்: ஒழுங்கற்ற வடிவமுடைய அட்டை, நூல், ஊசல் குண்டு, தாங்கி. ஒழுங்கற்ற வடிவமுடைய அட்டையில் மூன்று துளைகளை இடவும். படத்தில் காட்டியவாறு ஒரு துளையினைத் தாங்கியில் பொருத்தி அட்டையிதை; தொங்கவிடவும்.

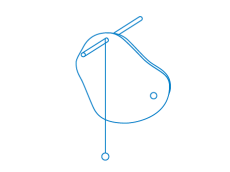
தாங்கியில் இருந்து அட்டையின் மேல்புறமாக அமையுமாறு குண்டுநூலினை தொங்கவிடவும்.

அட்டையின் மேல் குண்டுநூலின் நிலையினை ஒரு கோடாக வரைந்துகொள்ளவும்.

மேற்கூறியவாறு மற்ற இரு துளைகளையும் தாங்கியில் இருந்து தொங்கவிட்டுக் கோடுகள் வரைந்து கொள்ளவும்.

மூன்றுகோடுகளும் வெட்டும் புள்ளியின் நிலையினை X எனக் குறித்துக்கொள்ளவும்.

X என்ற புள்ளியே ஒழுங்கற்ற வடிவமுடைய அட்டையின் ஈர்ப்பு மையம் ஆகும்.

மீட்டர் அளவுகோலின் ஈர்ப்பு மையம்:

அளவுகோலானது ஒரு தாங்கியின் மீது அதன் ஈர்ப்பு மையத்தில் நிறுத்தப்படும் போது சமநிலையில் நிற்கிறது.

ஒழுங்கான வடிவமுடைய பொருளான அளவுகோல் போன்ற பொருள்களுக்கு அதன் வடிவியல் மையமே ஈர்ப்பு மையம் ஆகும்.

ஈர்ப்பு மையம் தவிர வேறு புள்ளியில் தாங்கியின் மீது வைக்கப்படும்போது அளவுகோலானது கவிழ்ந்து விடுகிறது.

சமநிலை:

ஒரு பொருளின் ஆரம்ப நிலையினைத் தக்க வைத்துக்கொள்ளும் திறனே அப்பொருளின் சமநிலை எனப்படும்.

சமநிலை மூன்று வகைப்படும்.

1. உறுதிச் சமநிலை.
2. உறுதியற்ற சமநிலை.
3. நடுநிலை சமநிலை.

உறுதிச் சமநிலை:

கூம்பானது மிக அதிகக் கோணத்திற்குச் சாய்க்கப்பட்டுப் பின்னர் விடப்பட்டாலும் கவிழ்ந்துவிடாமல் மீண்டும் பழைய நிலையை அடையும்.

கூம்பு சாய்க்கப்படும்போது அதன் ஈர்ப்பு மையம் உயர்கிறது. ஈர்ப்பு மையத்தின் வழியாக வரையப்படும் செங்குத்துக்கோடானது சாய்க்கப்பட்ட நிலையிலும் அதன் அடிப்பரப்பிற்கு உள்ளேயே விழுகிறது. எனவே அதனால் மீண்டும் தனது பழைய நிலையை அடைய முடிகிறது.

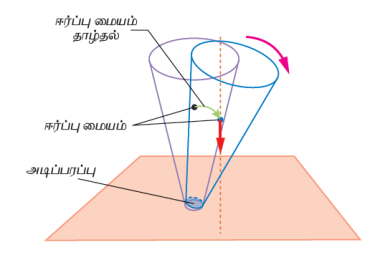
உறுதியற்ற சமநிலை:

கூம்பானது சிறிது சாய்க்கப்பட்டாலும் கவிழ்ந்துவிடும். கூம்பினைச் சாய்க்கும்போது ஈர்ப்பு மையம் அதன் நிலையிலிருந்து உயர்கிறது. ஈர்ப்பு மையம் வழியாக வரையப்படும் செங்குத்துக் கோடானது அதன் அடிப்பரப்பிற்கு வெளியே விழுகிறது. எனவே கூம்பானது கீழே கவிழ்கிறது.

நடுநிலை சமநிலை:

கூம்பானது உருள்கிறது. ஆனால் அது கீழே கவிழ்க்கப்படுவதில்லை.

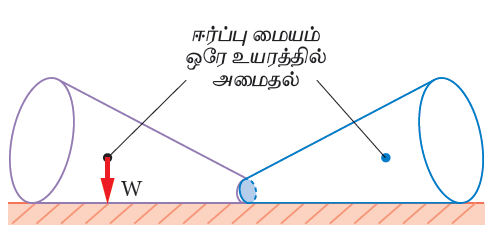
கூம்பினை நகர்த்தும்போது அதன் ஈர்ப்பு மையத்தின் உயரம் மாறுவதில்லை. கூம்பினை எவ்வாறு நகர்த்தினாலும் அதே நிலையிலேயே நீடித்து இருக்கிறது.

சுமநிலைக்கான நிபந்தனைகள்:

ஒரு பொருளின் சமநிலையை அதிகரிக்க

• அதன் ஈர்ப்பு மையம் குறைந்த உயரத்தில் அமைக்கப்பட வேண்டும்.
• பொருளின் அடிப்பரப்பினை அதிகரிக்க வேண்டும்.

ஈர்ப்பு மையம் அடிப்பரப்பின் முனையில் அமைகிறது. பெட்டியானது கீழே கவிழக்கூடிய நிலையில் காணப்படுகிறது. ஈர்ப்பு மையம் பொருளின் அடிப்பரப்பினுள் அமைகிறது.

கனமான அடிப்பகுதியானது அதன் ஈர்ப்பு மையத்தின் உயரத்தினைக் குறைக்கிறது. எனவே பெட்டியானது கீழே கவிழாது.

ஈர்ப்பு மையம் பொருளின் அடிப்பரப்பினுள் அமைகிறது. அகலமான அடிப்பரப்பானது பெட்டியைக் கவிழ்ப்பதைக் கடினமாக்குகிறது.

தஞ்சாவூர் பொம்மை

இது தஞ்சாவூரில் களிமண்ணால் செய்யப்படும் பழமைவாய்ந்த பாரம்பரிய பொம்மையாகும். பொம்மையின் ஈர்ப்பு மையமும் அதன் மொத்த எடையும் பொம்மையின் மிகக் கீழான அடிப்பகுதியில் அமையுமாறு செய்யப்படுகிறது. இதன் காரணமாகப் பொம்மையானது மிக மெல்லிய அலைவுடன் நடனம் போன்ற தொடர்ச்சியான இயக்கத்தினைத் தோற்றுவிக்கிறது.

ஈர்ப்பு மையத்தின் நடைமுறை பயன்பாடுகள்:

மேசை விளக்குகள், காற்றாடிகள் போன்றவற்றின் சமநிலையை அதிகரிப்பதற்காக அவற்றின் அடிப்பரப்பானது அகலமானதாகத் தயாரிக்கப்படுகின்றன.

சொகுசு பேருந்துகளின் மேற்பகுதியில் அல்லாமல் அடிப்பகுதியில் பொருள்கள் வைப்பு அறை அமைக்கப்படுகின்றன. இதன் மூலம் பேருந்தின் ஈர்ப்பு மையத்தின் உயரத்தினைக் குறைத்து அதன் சமநிலையை அதிகரிக்கலாம்.

இரண்டு அடுக்கு பேருந்துகளில் எவ்வளவு கூட்ட நெரிசல் இருக்கும்போதிலும் இரண்டாவது அடுக்கில் அனுமதிக்கப்பட்ட பயணிகளின் எண்ணிக்கையைத் தவிரக் கூடுதல் பயணிகள் அனுமதிக்கப்படுவதில்லை.

பந்தயக் கார்கள் உயரம் குறைவாகவும் அகலமானதாகவும் தயாரிக்கப்படுவதால் அதன் சமநிலை அதிகரிக்கப்படுகிறது.

இன்றைய அறிவியல்:

பொதுவான வேகங்கள்:

• ஆமை 0.1 மீ/வி.
• மனிதர்களின் நடையின் வேகம் 1.4 மீ/வி.
• விழும் மழைத்துளியின் வேகம் 9-10 மீ/வி.
• ஓடும் பூனையின் வேகம் 14 மீ/வி.
• சைக்கிளின் வேகம் 20-25 கி.மீ/மணி.
• சிறுத்தை ஓடும் வேகம் 3.1 மீ/வி.
• வேகம் பந்து வீச்சாளர்கள் பந்தினை எறியும் வேகம் 90-100 மைல்/மணி.
• பயணிகள் விமானத்தின் வேகம் 180 மீ/வி.
• ராக்கெட்டின் வேகம் 5200 மீ/வி.

நினைவில் கொள்க:

• தொலைவு – ஒரு இடத்திலிருந்து மற்றொரு இடத்திற்குப் பொருள் கடந்து வந்த மொத்தப் பாதை தொலைவு எனப்படும்.
• இடப்பெயர்ச்சி – ஒரு இடத்திலிருந்து மற்றொரு இடத்திற்கு இடையே உள்ள மிகக்குறைந்த நேர்க்கோட்டு பாதை இடப்பெயர்ச்சி எனப்படும்.
• இடப்பெயர்ச்சி மாறும் வீதம் திசைவேகம் எனப்படும். திசைவேகத்தின் SI அலகு மீட்டர்/விநாடி (மீ/வி) ஆகும்.
• திசைவேகம் மாறும் வீதம் முடுக்கம் எனப்படும். முடுக்கத்தின் SI அலகு மீ/வி²
• ஈர்ப்பு மையம் – எப்புள்ளியில் ஒரு பொருளின் எடை முழுவதும் செயல்படுவதுபோல் தோன்றுகிறதோ அப்புள்ளியே அப்பொருளின் ஈர்ப்பு மையம் எனப்படும்.
• ஒழுங்கான வடிவம் கொண்ட பொருள்களின் ஈர்ப்பு மையமானது பொதுவாக அதன் வடிவியல் மையத்தில் அமைகிறது.
• ஒரு பொருளின் ஆரம்ப நிலையினைத் தக்க வைத்துக்கொள்ளும் திறனே அப்பொருளின் சமநிலை எனப்படும்.
• சமநிலை மூன்று வகைப்படும்.

1. உறுதிச்சமநிலை.
2. உறுதியற்ற சமநிலை.
3. நடுநிலை சமநிலை.

உங்களுக்குத் தெரியுமா?

• 1 கிமீ/மணி = 5/18 மீ/வி இதனை எவ்வாறு நாம் பெறுகிறோம் என்பதனைக் காண்போம்.

1 கி.மீ = 1000 மீ

ஒரு மணி = 3600 வி

1 கிமீ/மணி = 1000 மீ/3600 வி = 5/18 மீ/வி.

நாட்டிகல் மைல்:

வான் மற்றும் கடல் வழி போக்குவரத்துகளில் தொலைவினை அளக்கப் பயன்படுத்தப்படும் அலகு நாட்டிக்கல் மைல் ஆகும். ஒரு நாட்டிக்கல் மைல் என்பது 1.852 கி.மீ ஆகும்.

கப்பல் மற்றும் விமானங்களின் வேகங்களை அளக்கப் பயன்படும் அலகு நாட் எனப்படும். ஒரு நாட் என்பது ஒரு மணி நேரத்தில் ஒரு நாட்டிக்கல் மைல் தொலைவு கடக்கத் தேவைப்படும் வேகம் ஆகும்.

சிறுத்தையான நான் மிக வேகமாக ஓடும் விலங்கு ஆவேன். எனது வேகம் 25 மீ/வி முதல் 30 மீ/வி வரை ஆகும். என்னால் இரண்டு விநாடியில் எனது வேகத்தினை 0 விலிருந்து 20 மீ/வி ஆக மாற்றிக் கொள்ள முடியும்.