இயக்கம் Notes 9th Science Lesson 2 Notes in Tamil
இயக்கம் Notes 9th Science Lesson 2 Notes in Tamil
அறிமுகம்
- இயக்கம் என்பது ஒரு பொருளின் சுற்றுப்புறத்தைப் பொறுத்து அதன் நிலையில் ஏற்படும் மாற்றம் ஆகும். இந்த அண்டத்திலுள்ள அனைத்துப் பொருட்களும் இயக்கத்தில் உள்ளன. ஒரு பொருளானது இயங்காதது போல் தோன்றினாலும், உண்மையிலேயே அதுவும் இயக்கத்தில் உள்ளது.
- ஏனென்றால், பூமியானது சூரியனைச் சுற்றி வருகிறது. உங்களைச் சுற்றியுள்ள பொருள்கள் இயக்கத்தில் இருப்பதைக் காணலாம். சாலையில் செல்லும் வாகனங்கள், தண்டவாளத்தில் செல்லும் தொடர் வண்டி, வானத்தில் பறக்கும் விமானம் ஆகிய யாவும் இயங்குகின்றன. இந்த இயக்கங்கள் ஒரு வகை இயக்கமாகும்.
- வீட்டின் மேற்கூரை மீது மின்விசிறி சுற்றுவதைப் பார்த்திருப்பீர்கள். இரு ஒரு வகை இயக்கம். நீங்கள் ஊஞ்சலில் ஆடும்போது, அது முன்னும், பின்னும் செல்கிறது. இதுவும் ஒரு வகை இயக்கம். இயக்கமானது, தொலைவு, வேகம், முடுக்கம் மற்றும் காலத்தால் வரையறுக்கப்படுகிறது. இந்தப் பாடத்தில் இயக்கத்தின் வகைகளைப் பற்றியும், இயக்கச் சமன்பாடுகள் பற்றியும் நீங்கள் படிக்க இருக்கிறீர்கள்.
ஓய்வு மற்றும் இயக்க நிலை
- இயற்பியலில், பொருட்களின் நிலை மாறாமல் இருந்தால் அவை ஓய்வாக உள்ளன எனப்படும். பொருட்கள் அதன் நிலையிலிருந்து மாறிக் கொண்டிருப்பின் அவை இயங்குகின்றன எனப்படும்.
- உதாரணமாக, ஒரு மேசையின் மேல் இருக்கும் புத்தகம், அறையில் உள்ள சுவர்கள் ஆகியவை ஓய்வு நிலையில் உள்ளன. சாலையில் ஓடுகின்ற கார் மற்றும் பேருந்துகள், காற்று வெளியில் பறந்து கொண்டிருக்கின்ற பறவைகள் மற்றும் விமானங்கள் ஆகியவை இயக்க நிலையில் உள்ளன. இயக்கம் என்பது ஒரு சார்பியல் நிகழ்வு. அதாவது ஒரு மனிதருக்கு இயக்கத்தில் இருப்பது போலத் தோன்றும். ஆனால், சாலையில் நின்று கொண்டிருக்கும் ஒரு மனிதருக்கு அதே மரங்கள் நகராமல் இருப்பது போல் தோன்றும்.
இயக்கத்தின் பல்வேறு வகைகள்
இயற்பியலில் இயக்கத்தைக் கீழ்க்கண்டவாறு வகைப்படுத்தலாம்.
நேரான இயக்கம் : நேர்க்கோட்டில் செல்லும் பொருளின் இயக்கம்.
வட்ட இயக்கம் : வட்டப்பாதையில் செல்லும் பொருளின் இயக்கம்.
அலைவு இயக்கம் : ஒரு புள்ளியை மையமாகக் கொண்டு மீண்டும் மீண்டும் முன்னும் பின்னுமாக இயங்கும் பொருளின் இயக்கம்.
ஒழுங்கற்ற இயக்கம்: மேலே குறிப்பிட்ட எந்த இயக்கத்தையும் சாராத இயக்கம்.
சீரான மற்றும் சீரற்ற இயக்கம்
சீரான இயக்கம்
மகிழுந்து ஒன்று, முதல் ஒரு மணி நேரத்தில் 60 கி.மீ தொலைவையும், இரண்டாவது ஒரு மணி நேரத்தில் 60 கி.மீ தொலைவையும், மூன்றாவது ஒரு மணி நேரத்தில் மேலும் 60 கி.மீ தொலைவையும் கடப்பதாகக் கொள்வோம். அந்த மகிழுந்தானது, சமகால இடைவெளியில் சம தொலைவைக் கிடக்கின்றது. அந்த மகிழுந்தின் இயக்கத்தை சீரான இயக்கம் என்று நாம் கூறலாம்.
ஒரு பொருள் நகரும் பொழுது சமமான தொலைவுகளை சமகால இடைவெளிகளில் கடந்தால் அது சீரான இயக்கத்தை மேற்கொண்டிருக்கிறது எனக் கூறலாம். சீரான கால இடைவெளிகளின் அளவு மிகச் சிறியதாகவோ அல்லது மிகப் பெரியதாகவோ இருக்கலாம்.
சீரற்ற இயக்கம்
ஒரு பேருந்து நிறுத்தத்திலிருந்து புறப்படும் பேருந்து ஒன்றைக் கருதுவோம். கூட்ட நெரிசல் மிகுந்த பகுதியில் அது மெதுவாகச் சென்று கொண்டிருக்கிறது. நெரிசல் மிகுந்த காரணத்தினால் அப்பேருந்து 5 நிமிடத்தில் 100மீ தொலைவை மட்டுமே கடக்கிறது. அப்பகுதியைக் கடந்து வெளியே வந்தபோது, சாலையில் வாகன நெரிசல் இல்லாததால் அதன் வேகம் அதிகரித்து, 5 நிமிடத்தில் 2 கி.மீ தொலைவைக் கடக்கிறது. இப்பேருந்தின் இயக்கத்தை சீரற்றது எனக் குஊறலாம். ஏனெனில், அது சமமற்ற தொலைவுகளை சமகால இடைவெளிகளில் கடந்துள்ளது.
ஒரு பொருள் சமகால இடைவெளிகளில் சமமற்ற தொலைவுகளைக் கடந்தால் அது சீரற்ற இயக்கத்தை மேற்கொண்டுள்ளது என்று கூறலாம்.
தொலைவு மற்றும் இடப்பெயர்ச்சி
A என்ற புள்ளியிலிருந்து பொருள் ஒன்று நகர்வதாகக் கருதுவோம். அது படத்தில் கொடுக்கப்பட்டுள்ள பாதையில் நகர்ந்து B என்ற புள்ளியை அடைகின்றது. A என்ற புள்ளுயிலிருந்து B என்ற புள்ளி வரை அப்பொருள் கடந்த மொத்த நீளம் அப்பொருள் கடந்த தொலைவு ஆகும். AB என்ற கோட்டின் நீளம் இடப்பெயர்ச்சி ஆகும்.
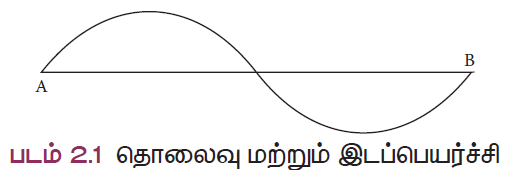
தொலைவு
திசையைக் கருதாமல், ஒரு நகரும் பொருள் கடந்த பாதையின் நீளமே, அப்பொருள் கடந்த தொலைவு எனக் கூறலாம். SI முறையில் அதை அளக்கப் பயன்படும் அலகு ‘மீட்டர்’. தொலைவு என்பது எண்மதிப்பை மட்டும் கொண்ட திசையிலி (ஸ்கேலார்) அளவுரு ஆகும்.
இடப்பெயர்ச்சி
ஒரு குறிப்பிட்ட திசையில், இயங்கும் பொருளொன்றின் நிலையில் ஏற்படும் மாற்றமே இடப்பெயர்ச்சி ஆகும். இது எண்மதிப்பு மற்றும் திசை ஆகிய இரண்டையும் கொண்ட திசையளவுரு (வெக்டர்) ஆகும். SI அலகு முறையில் இடப்பெயர்ச்சியின் அலகும் மீட்டர் ஆகும்.
வேகம், திசைவேகம் மற்றும் முடுக்கம்
வேகம் என்பது எவ்வளவு விரைவாக பொருள் ஒன்று இயங்குகிறது என்பதைக் குறிக்கிறது. ஆனால், திசைவேகம் என்பது வேகத்தையும், அப்பொருள் நகரும் திசையையும் குறிக்கிறது.
வேகம்
வேகம் என்பது தொலைவின் மாறுபாட்டு வீதம் அல்லது ஓரலகு நேரத்தில் கடந்த தொலைவு எனப்படும். இது ஒரு ஸ்கேலார் அளவாகும். SI அளவீட்டு முறையில் வேகத்தின் அலகு மீவி-1
வேகம் = கடந்த தொலைவு / எடுத்து கொண்ட நேரம்
திசைவேகம்
திசைவேகம் என்பது இடப்பெயர்ச்சியின் மாறுபாட்டு வீதம் அல்லது ஓரலகு நேரத்திற்கான இடப்பெயர்ச்சி எனப்படும். இது ஒரு வெக்டர் அளவாகும். SI அளவீட்டு முறையில் திசை வேகத்திற்கான அலகும் மீவி-1 ஆகும். இதன்படி
திசைவேகம் =
முடுக்கம்
முடுக்கம் என்பது திசைவேக மாறுபாட்டு வீதம் அல்லது ஓரலகு நேரத்தில் ஏற்படும் திசைவேக மாறுபாடு எனப்படும். இது ஒரு வெக்டர் அளவாகும். SI அளவீட்டு முறையில் முடுக்கத்தின் அலகு மீவி-2.
முடுக்கம் =
=
பொருள் ஒன்று தனது திசையை மாற்றாமல் நேர்கோட்டில் இயங்கும் ஒரு நிகழ்வினைக் கருதுவோம். மேலே கொடுக்கப்பட்ட சமன்பாட்டிலிருந்து v > u எனில், அதாவது, இறுதித் திசைவேகம், தொடக்கத் திசைவேகத்தை விட அதிகமாக இருந்தால், திசைவேகமானது நேரம் செல்ல செல்ல அதிகரிக்கும் மேலும் முடுக்கம் நேர்மதிப்பு பெறும்.
ஒருவேளை, v < u, அதாவது இறுதித் திசைவேகம், தொடக்க திசைவேகத்தை விடக் குறைவாக இருந்தால், திசைவேகமானது நேரம் செல்லச் செல்ல குறையும் மற்றும் முடுக்கம் எதிர்மதிப்பு பெறும். இது எதிர்முடுக்கம் எனப்படும். எதிர் முடுக்கத்தை வேக இறக்கம் அல்லது ஒடுக்கம் எனலாம். உதாரணமாக, முடுக்கத்தின் மதிப்பு – 2 மீவி-2 எனில் அதை எதிர் முடுக்கம் என்று கூறலாம். v = u, எனில் a = 0. அதாவது, இறுதித் திசைவேகம் தொடக்க திசைவேகத்திற்குச் சமமாக இருக்கும் பொழுது முடுக்கம் சுழியாகும்.
நேர்கோட்டு இயக்கத்தின் வரைபட விளக்கம்
தொலைவு / இடப்பெயர்ச்சி அல்லது வேகம்/ திசைவேகம் சார்ந்த வரைபடத்தை வரைவதிலிருந்து காலம் மற்றும் நிலை பற்றிய கருத்துக்களை நாம் புரிந்து கொள்ள இயலும்.
சீரான இயக்கத்திற்கான தொலைவு – காலம் வரைபடம்
வெவ்வேறு காலத்தில் ஒரு நபர் நடந்த தூரத்தினைக் காட்டும் அட்டவணையைக் கருதுவோம்.
சீரான இயக்கம்
| காலம் (நிமிடத்தில்) | தொலைவு (மீட்டர்) |
| 0 | 0 |
| 5 | 500 |
| 10 | 1000 |
| 15 | 1500 |
| 20 | 2000 |
| 25 | 2500 |
நடக்க எடுத்துக்கொண்ட காலத்தை X- அச்சிலும், கடந்த தொலைவை Y – அச்சிலும் எடுத்துக் கொண்டு ஒரு வரைபடம் வரையப்படுகிறது. இந்த வரைபடம் தொலைவு – கால வரைபடம் எனப்படும்.
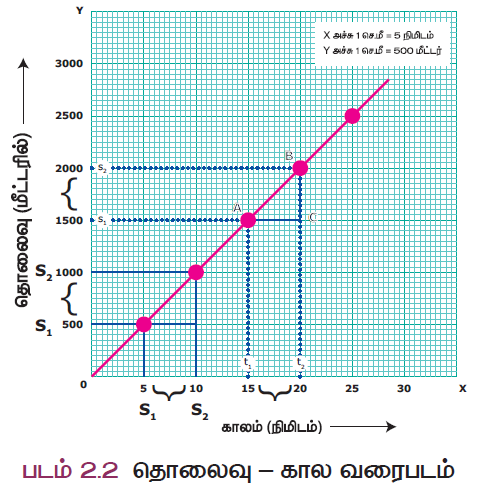
தொலைவு – கால வரைபடத்தைக் கவனித்தால் நாம் சில கருத்துக்களைப் புரிந்து கொள்ளலாம். முதலாவதாக, அந்த நபர் கடந்த தொலைவிற்கும் காலத்திற்கும் இடையேயுள்ள தொடர்பு வரைபடத்தாளில் ஒரு நேர்கோடாக இருக்கிறது. மேலும், அவர் சமகால இடைவெளிகளில் சம தொலைவுகளைக் கடந்து சென்றதையும் அறிந்து கொள்ள முடிகிறது. இதிலிருந்து அந்த நபர் மாறாத வேகத்தில் நடந்து சென்றதைத் தீர்மானிக்கலாம்.
வரைபடத்தாளிலிருந்து, அந்த நபர் நடந்து சென்ற வேகத்தை நீங்கள் கணக்கிட்டுக் கூறமுடியுமா? ஆம் உங்களால் முடியும். அது பண்பளவில் நேர்கோட்டின் சாய்வாக அமைகிறது.
நடைவேகம் =
= BC / AC (வரைபடத்திலிருந்து)
= நேர்கோட்டின் சாய்வு
= 500 / 5 = 100 மீ/வி
அதாவது சாய்வு அதிகரிக்க அதிகரிக்க (அதிக மதிப்பு) வேகமும் அதிகரிக்கிறது.
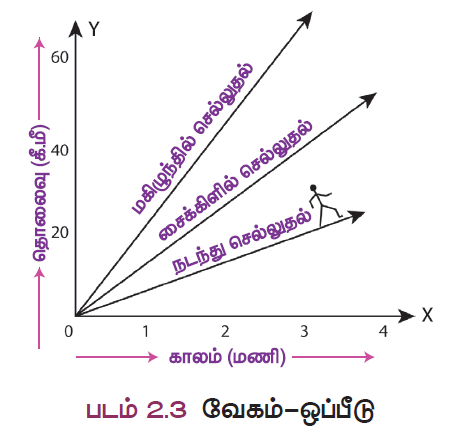
- ஒரே பாதையில் செல்லும் ஆசேரின் நடைப்பயணம், சாஃபிராவின் மிதிவண்டிப் பயணம் மற்றும் கனிஷ்காவின் மகிழுந்துப் பயணத்திற்கான தொலைவு – கால வரைபடத்தினைப் பார்ப்போம் (படம்).
- நடை வேகத்தைக் காட்டிலும் மிதிவண்டியின் வேகம் அதிகமாகவும், அதைக் காட்டிலும் மகிழுந்தின் வேகம் அதிகமாகவும் இருக்கும் என்பது நமக்குத் தெரியும். மூன்று பயணங்களின் தொலைவு – கால வரைபடங்கள் படத்தில் காட்டியது போல இருக்கும். வேகம் அதிகரிக்க அதிகரிக்க தொலைவு – கால வரைபடத்தில் நேர்கோட்டின் சாய்வும் அதிகரிக்கிறது.
சீரற்ற இயக்கத்திற்கான தொலைவு – காலம் வரைபடம்
முடுக்குவிக்கப்பட்ட இயக்கத்திற்கான தொலைவு – காலம் வரைபடத்தையும் நாம் வரையலாம் (சீரற்ற இயக்கம்). பின்வரும் அட்டவணையானது , ஒரு மகிழுந்து இரண்டு விநாடி கால இடைவெளிகளில் கடந்து சென்ற தொலைவைக் காட்டுகிறது.
சீரற்ற இயக்கம்
| காலம் (நிமிடத்தில்) | தொலைவு (மீட்டர்) |
| 0 | 0 |
| 2 | 1 |
| 4 | 4 |
| 6 | 9 |
| 8 | 16 |
| 10 | 25 |
| 12 | 36 |
கடந்த தொலைவு மற்றும் எடுத்துக் கொண்ட நேரம் ஆகியவற்ரிற்கான ஒரு வரைபடத்தை நாம் வரைந்தால் அது படத்தில் காட்டப்பட்டுள்ளது அமையும்.
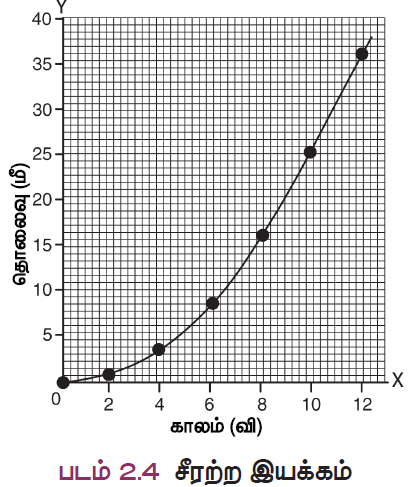
வரைபடம் சீரான இயக்கத்தில் கிடைத்த நேர்கோடு போல இல்லை. இந்த வரைபடமானது, கடந்த தொலைவு மற்ரும் எடுத்துக்கொண்ட நேரத்திற்கான, நேரியல் சார்பற்ற (non linear) மாற்றத்தைக் குறிக்கிறது. எனவே, இந்த வரைபடம் சீரற்ர வேகத்திற்கான இயக்கத்தைக் காட்டுகிறது.
திசைவேகம் – காலம் வரைபடம்
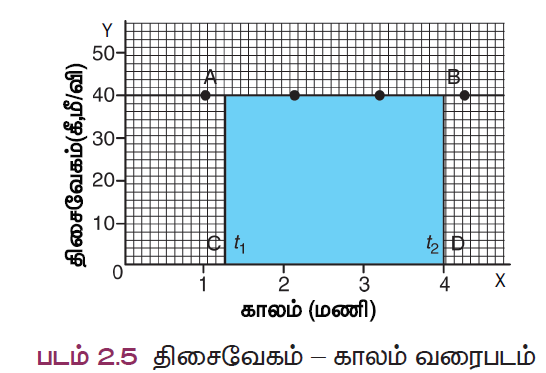
பொருளொன்றின் திசைவேகம் காலத்தைச் சார்ந்து எப்படி மாறுகிறது என்பதை திசைவேகம் – காலம் வரைபடத்திலிருந்து அறியலாம். இந்த வரைபடத்தில் காலம் X அச்சிலும், திசைவேகம் Y அச்சிலும் குறிப்பிடப்படுகிறது. பொருள் ஒன்று சீரான திசைவேகத்தில் சென்றால் X அச்சுக்கு இணையான ஒரு நேர்கோடு கிடைக்கும். பின்வரும் வரைபடம் மகிழுந்து ஒன்று 40 கி.மீ./ மணி என்ற சீரான திசைவேகத்தில் பயணிப்பதைக் காட்டுகிறது.
ஒரு பொருள் சீரான திசைவேகத்தில் செல்லும்போது, அதன் திசைவேகத்தையும் கால இடைவெளியையும் பெருக்கினால், கிடைப்பது அப்பொருளின் இடப்பெயர்ச்சி என்பது நாம் அறிந்ததே. எனவே, திசைவேகம் – காலம் வரைகோட்டில் கிடைக்கும் பரப்பளவு இடப்பெயர்ச்சியின் எண் மதிப்பிற்குச் சமமாகும். ஆகவே ‘t’ என்ற கால இடைவெளியில், மகிழுந்தின் இடப்பெயர்ச்சி S கீழ்க்கண்டவாறு கணக்கிடப்படுகிறது,.
S = AC X CD
S = செவ்வகம் ABCD-ன் பரப்பளவு (வரைபடத்தில் நிழலாக்கப்பட்ட பகுதி)
சீராக முடுக்கப்பட்ட இயக்கத்தினையும் அதன் திசைவேகம் – காலம் வரைபடத்தை வரைவதிலிருந்து அறியலாம். நேரான சாலையில் இயக்கப்படும் மகிழுந்து ஒன்றைக் கருதுவோம். வேகமானியின் மூலம், ஒவ்வொரு விநாடி காலத்திலும் அதன் திசைவேகமானது பதிவு செய்யப்படுகிறது. வெவ்வேறு கால இடைவெளியில் மகிழுந்தின் திசைவேகம் (மீ/விநாடி) அட்டவணையில் பின்வருமாறு கொடுக்கப்பட்டுள்ளது.
சீராக முடுக்கப்பட்ட இயக்கம்
| காலம் (விநாடி) | மகிழுந்தின் திசைவேகம் (மீ/விநாடி) |
| 0 | 0 |
| 5 | 9 |
| 10 | 18 |
| 15 | 27 |
| 20 | 36 |
| 25 | 45 |
| 30 | 54 |
மகிழுந்தின் இயக்கத்திற்கான திசைவேகம்-காலம் வரைபடம் படத்தில் காட்டப்பட்டுள்ளது. சம கால இடைவெளியில் திசைவேகமானது சம அளவு மாறுபடுவதை வரைபடம் காட்டுகிறது. ஆகவே, சீரான முடுக்கப்பட்ட இயக்கங்கள் அனைத்திற்கும் திசைவேகம் – காலம் வரைபடம் ஒரு நேர்கோடாக அமையும்.
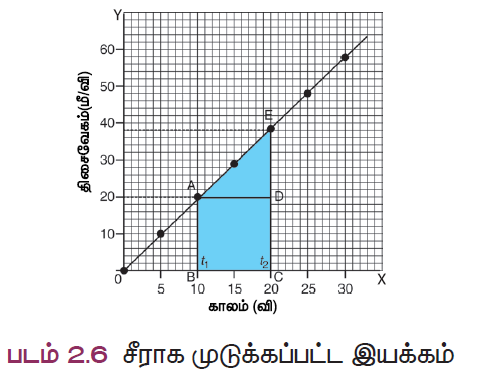
திசைவேக – காலம் வரைபடத்திலிருந்து மகிழுந்து எவ்வளவு தொலைவு சென்றுள்ளது என்பதையும் முடிவு செய்யலாம். திசைவேகம் – காலம் வரைபடத்தில் உள்ள பரப்பளவானது, மகிழுந்து ஒன்று கொடுக்கப்பட்ட கால இடைவெளியில் கடந்து சென்ற தொலைவைக் (இடப்பெயர்ச்சியின் எண்மதிப்பு) குறிக்கும்.
மகிழுந்தின் திசைவேகத்தின் எண்மதிப்பு அதன் முடுக்கத்தினால் மாறுவதால் மகிழுந்து பயணம் செய்த தொலைவானது, திசைவேகம் – காலம் வரைபடத்தில் உள்ள பரப்பளவு ABCDE மூலம் கொடுக்கப்படுகிறது.
S = பரப்பளவு ABCDE
S = செவ்வகத்தின் பரப்பளவு ABCD + முக்கோணத்தின் பரப்பளவு ADE
S = (AB X BC) + ½ (AD X DE)
நாற்கரம் ABCDE இன் பரப்பளவை, சரிவகம் ABCDE இன் பரப்பளவிலிருந்தும் கணக்கிடலாம். அதாவது,
S = சரிவகம் ABCDE யின் பரப்பளவு
= ½ X (இணைப்பக்க நீளங்களின் கூட்டல்) X (இணைப்பக்கங்களுக்கு இடைப்பட்ட தொலைவு)
S = ½ X (AB + CE) X BC
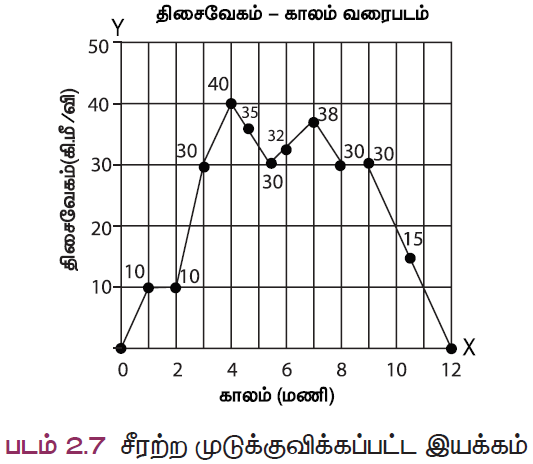
கீழ்க்கண்ட வரைபடத்தில் காட்டப்பட்டுள்ளது போல சீரற்ற முடுக்குவிக்கப்பட்ட இயக்கத்தில், தொலைவு – காலம் மற்றும் திசைவேகம் – காலம் வரைபடங்கள் எந்த இரு வடிவத்தையும் கொண்டிருக்கும்.
- வாகனத்தில் உள்ள வேகமானி ஒரு குறிப்பிட்ட கண நேரத்தில் நிகழும் வேகத்தை அளக்கும். ஒருபரிமாண சீரான இயக்கத்தில் சராசரித் திசைவேகமும் உடனடித் திசைவேகமும் சமம். எந்த ஒரு கணத்திலும் கணக்கிடப்படும் உடனடித் திடைவேகம் என்பதை அப்பொருளின் திசைவேகம் என்றும் உடனடி வேகம் என்றும் கூறலாம்.
இயக்கச் சமன்பாடுகள்
நியூட்டன், ஒரு பொருளின் இயக்கத்தை ஆய்வு செய்ததன் விளைவாக மூன்று சமன்பாடுகளின் தொகுப்பை வழங்கினார். இந்தச் சமன்பாடுகள் இயக்கத்தில் இருக்கும் ஒரு பொருளின் இடப்பெயர்ச்சி, திசைவேகம், முடுக்கம் மற்றும் நேரம் ஆகியவற்றிற்கிடையேயான தொடர்பினைக் கூறுகின்றன. ‘a’ என்ற முடுக்கத்தினால் இயங்கும் பொருள் ஒன்று ‘t’ காலத்தில் ‘u’ என்ற தொடக்க திசை வேகத்திலிருந்து ‘v’ என்ற இறுதித் திசைவேகத்தை அடைகிறது. அப்போது அதன் இடப்பெயர்ச்சி ‘s’ எனில் இயக்கச் சமன்பாடுகளை கீழ்க்கண்டவாறு எழுதலாம்.
v = u + at
S = ut + ½ at2
v2 = u2 + 2as
இயக்கத்தில் இருக்கும் ஒரு பொருளுக்கு வரைபட முறையின் மூலம் இந்த சமன்பாடுகளைப் பெற முடியும்.
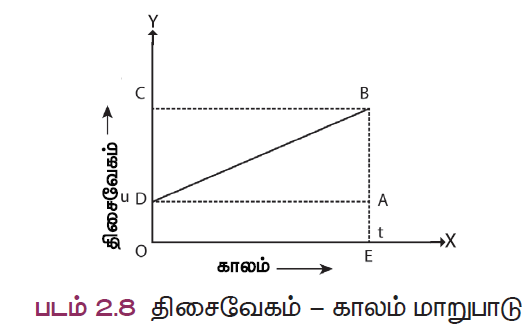
மேற்கண்ட வரைபடம் சீராக முடுக்கப்பட்ட பொருள் ஒன்று காலத்தைப் பொறுத்து அடையும் திசைவேக மாற்றத்தைக் காண்பிக்கிறது. வரைபடத்தில் ‘D’ என்ற தொடக்கப் புள்ளியிலிருந்து ‘u’ என்ற திசை வேகத்துடன் இயங்கும் பொருளொன்றின் திசைவேகம் தொடர்ச்சியாக அதிகரித்து ‘t’ காலத்திற்குப்பின் ‘B’ என்ற புள்ளியை அப்பொருள் அடைகிறது.
பொருளின் தொடக்க திசைவேகம் = u = OD = EA
பொருளின் இறுதித் திசைவேகம் = v = OC = EB
காலம் = t = OE = DA
வரைபடத்திலிருந்து AB = DC ஆகும்.
முதல் இயக்கச் சமன்பாடு
வரையறைப்படி முடுக்கம் (a)
=
=
at =
DC = at = AB
வரைபடத்திலிருந்து, EB = EA + AB
v = u + at (1)
இது முதல் இயக்கச் சமன்பாடு ஆகும்.
இரண்டாம் இயக்கச் சமன்பாடு
வரைபடத்திலிருந்து ‘t’ காலத்தில் பொருள் ஒன்று கடந்த தொலைவான நாற்கரத்தின் பரப்பளவு DOEB மூலம் கொடுக்கப்படுகிறது.
S = நாற்கரத்தின் பரப்பளவு DOEB
= செவ்வகத்தின் பரப்பளவு DOEA + முக்கோணத்தின் பரப்பளவு DAB
= (AE x OE) + ½ X (AB X DA)
S = ut + ½ at2 (2)
இது இரண்டாம் இயக்கச் சமன்பாடு ஆகும்.
மூன்றாவது இயக்கச் சமன்பாடு
‘t’ காலத்தில் பொருள் கடந்த தொலைவை வரைபடத்தில் நாற்கரம் DOEB யின் பரப்பளவானது குறிக்கிறது. இங்கு DOEB என்பது சரிவகத்தையும் குறிக்கிறது.
S = சரிவகம் DOEB யின் பரப்பளவு
= ½ X இணைப் பக்க நீளங்களின் கூடுதல் X இணைப் பக்கங்களுக்கு இடைப்பட்ட தொலைவு
= ½ X (OD + BE) X oe
S= ½ X (u + v) x t
ஆனால், முடுக்கம் a = (v –u)/t அல்லது
t = (v –u) / a
எனவே, s = / x (v + u) x (v – u) /a
2as = v2 – u2
v2 = u2 + 2as (3)
இது மூன்றாம் இயக்கச் சமன்பாடு ஆகும்.
தடையின்றி தானே விழும் பொருளி ன் இயக்கம்
ஒரு பெரிய கல் மற்றும் சிறிய அழிப்பான் இரண்டையும் எடுத்துக் கொள்க. ஒரு மேசையின் மீது நின்று கொண்டு அந்த இரண்டு பொருட்களையும் ஒரே உயரத்திலிருந்து ஒரே நேரத்தில் கீழே விடவும். நீங்கள் காண்பது என்ன? இப்பொழுது, ஒரு சிறிய அழிப்பான் மற்றும் ஒரு காகிதத் தாள் இரண்டையும் எடுத்துக்கொள்க. ஒரு மேசையின் மீது நின்று கொண்டு அந்த இரண்டு பொருட்களையும் ஒரே உயரத்திலிருந்து ஒரே நேரத்தில் கீழே விடவும். என்ன காண்கிறீர்கள்? இப்பொழுது , சமமான நிறையுடைய இரண்டு காகிதத் தாள்களை எடுத்துக் கொள்க. இதில் ஒன்றை மட்டும் கசக்கி பந்து போல் சுருட்டிக் கொள்க. இப்பொழுது இரண்டையும் ஒரே உயரத்தில் இருந்து ஒரே நேரத்தில் கீழே விடவும். இப்பொழுது என்ன நடைபெறுகிறது?
கல் மற்றும் அழிப்பான் இரண்டும் பூமியின் மேல்பரப்பை சற்றேறக்குறைய ஒரே நேரத்தில் வந்தடைந்தன என்பதைக் காண முடியும். ஆனால், அழிப்பானையும், காகிதத்தையும் கீழே விடும் பொழுது அழிப்பான் முதலில் வந்தடைகிறது. காகிதத்தாள் பின்னர் வந்தடைகிறது. அதைப்போலவே காகிதத்தாளும், பந்துபோல் சுருட்டப்பட்ட காகிதமும் ஒரே எடையைப் பெற்றிருந்த போதும், பந்து போல் சுருட்டப்பட்ட காகிதம் முதலாவதும், காகிதத் தாள் இரண்டாவதும் தரையை வந்தடைவதைக் காணலாம். இதற்கான காரணம் உங்களுக்குத் தெரியுமா? காற்றில்லாத வெற்றிடத்தில் மேற்சொன்ன அனைத்துப் பொருட்களும் ஒரே நேரத்தில் தரையை வந்தடையும். காற்று ஊடகத்தில் காற்றின் உராய்வு விசையானது தடையின்றி தானே விழும் பொருளின் மீது ஒரு தடையை ஏற்படுத்துகிறது.
அழிப்பான் மற்றும் கல்லின் மீது செயல்படும் இந்த காற்றுத்தடை புவிஈர்ப்பு விசையுடன் ஒப்பிடும்போது புறக்கணிக்கத் தக்கதாகும். எனவே அவையிரண்டும் ஏறத்தாழ ஒரே நேரத்தில் தரையை வந்தடைகின்றன. இந்த செயல்பாடுகளின் மூலம், காற்றுத் தடையின் அளவானது, பொருளின் பரப்பளவைப் பொறுத்துள்ளது என்பதை அறியலாம்.
தடையின்றி கீழே விழும் பொருட்கள் முடுக்கமடையும் என்பது நமக்குத் தெரிந்ததே. இந்த முடுக்கம் பொருளின் நிறையைப் பொருத்தது அல்ல. அதாவது , உள்ளீடற்ற பொருள் அல்லது திடப்பொருள் மற்றும் சிறிய அல்லது பெரிய பொருட்கள் அனைத்தும் ஒரே கால வீதத்தில் கீழே விழும். முடுக்கம் ‘a’ க்குப் பதிலாக புவிஈர்ப்பு முடுக்கம் ‘g’ ஐப் பிரதியிடுவதால், தடையின்றி தானே கீழே விழும் பொருட்களுக்கான சமன்பாடுகளைப் பெற முடியும் . தடையின்றி தானே விழும் பொருட்களுக்கு அதன் ஆரம்பத் திசைவேகம் u = 0. எனவே, கீழ்க்காணும் சமன்பாடுகளைப் பெற முடியும்.
v = gt, s = ½ gt2 , v2 = 2gh
ஒரு பொருளை மேல்நோக்கி எறியும் பொழுது அது, புவியீர்ப்பு விசைக்கு எதிர்த்திசையில் செல்கிறது. எனவே, ‘a’ க்கு பதிலாக –g என்றும் எடுத்துக்கொள்ள வேண்டும். கீழ்நோக்கிச் செல்லும்போது, +g என எடுத்துக்கொள்ள வேண்டும்.
ஒரு பொருள் சுழி திசைவேகம் மற்றும் வரையறுக்கப்பட்ட முடுக்கத்தைக் கொண்டிருக்க முடியுமா? ஆம், ஒரு பொருளை செங்குத்தாக மேல் நோக்கி எறிந்தால், பொருளின் திசைவேகம் படிப்படியாகக் குறைந்து, பெரும உயரத்தை அடைந்த நிலையில் சுழி மதிப்பைப் பெறுகிறது. அப்போது அப்பொருளின் முடுக்கம் புவிஈர்ப்பு முடுக்கத்துக்குச் சமமாக இருக்கும்.
சீரான வட்ட இயக்கம்
ஒர் பொருள் வட்ட வடிவப் பாதையில் செல்லும்போது அதன் திசை ஒவ்வொரு புள்லியிலும் மாறிக் கொண்டே இருக்கும்.
பொருள் ஒன்று வட்டப்பாதையில் மாறாத வேகத்தில் செல்லும் பொழுது, திசை மாறுவதால், திசைவேகமும் மாறுகின்றது. எனவே, இது ஒரு முடுக்குவிக்கப்பட்ட இயக்கமாகும். உதாரணமாக, பூமி சூரியனைச் சுற்றி வருவது, நிலவு பூமியைச் சுற்றி வருவது, கடிகாரத்தின் வினாடி முள்ளின் இயக்கம் ஆகியவை சீரான வட்ட இயக்கங்களாகும்.
‘r’ ஆரம் கொண்ட வட்டப் பாதையில் சுற்றிவரும் ஒரு பொருளானது, ஒரு சுற்றுக்குப்பின் தொடக்க நிலைக்கு திரும்பிவர எடுத்துக்கொண்ட காலம் ‘T’ எனில் அதன் வேகம் ‘V’ பின்வருமாறு கணக்கிடப்படுகிறது.
வேகம் V = சுற்றளவு / எடுத்துக்கொண்ட காலம்
V = 2r /T
மையநோக்கு முடுக்கம் மற்றும் மையநோக்கு விசை
ஒரு பொருளினுடைய திசைவேகத்தின் எண் மதிப்பு அல்லது திசை அல்லது இரண்டுமே மாறுபட்டால் அப்பொருள் முடுக்கப்படுகிறது எனலாம். ஆகவே, வட்டப்பாதையில் மாறாத வேகத்தில் செல்லும் கல் ஒன்று முடுக்கப்பட்ட இயக்கத்தைக் கொண்டுள்ளது. இங்கு கயிற்றின் வழியே செயல்படும் உள்நோக்கிய முடுக்கமானது கல்லை வட்டப்பாதையில் இயங்க வைக்கிறது. இந்த முடுக்கத்தை மையநோக்கு முடுக்கம் என்றும் அதனுடன் தொடர்புடைய விசையை மையநோக்கு விசை என்றும் கூறுகிறோம். மையநோக்கு முடுக்கம் வட்டத்தின் மையத்தை நோக்கி செயல்படுவதால் மையநோக்கு விசையும் ஆரத்தின் வழியே அதே திசையில் பொருளின் மீது செயல்படும்.
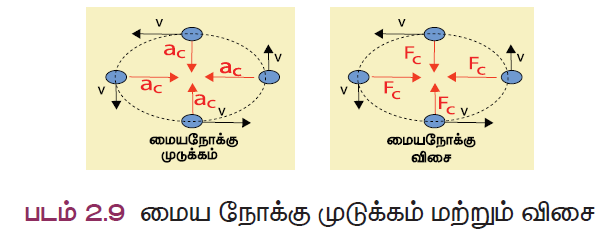
‘m’ நிறை உடைய ஒரு பொருள் ‘r’ ஆரமுடைய ஒரு வட்டப் பாதையில், ‘v’ திசைவேகத்தில் செல்வதாகக் கருதினால், அதன் மையநோக்கு முடுக்கமானது,
a = v2/r
மையநோக்கு விசையின் எண் மதிப்பு
F = நிறை x மைய நோக்கு முடுக்கம்
F = mv2 /r
- ஈர்ப்பு விசை, உராய்வு விசை, காந்த விசை, நிலை மின்னியல் விசை மற்றும் இதுபோன்ற எந்த ஒரு விசையும் மையநோக்கு விசை போன்று செயல்படும்.
மையவிலக்கு விசை
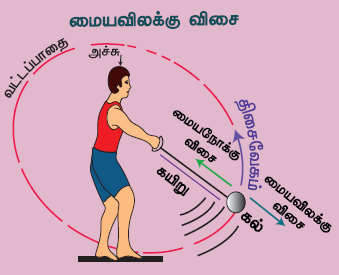
ஒரு கயிற்றை எடுத்துக்கொண்டு அதன் ஒரு முனையில் கல் ஒன்றைக் கட்டவும். கயிற்றின் மறு முனையைக் கைகளினால் பிடித்துக்கொண்டு சுற்றும்போது அக்கல்லானது வட்டப்பாதையை மேற்கொள்ளும். உங்கள் கைகளில் தள்ளு விசையையோ அல்லது இழுப்பு விசையையோ நீங்கள் உணர்கிறீர்களா?
இச்செயலில் ஒரு இழு விசையானது மையத்திலிருந்து வெளிநோக்கிச் செயல்படுவதை உணர்ந்திருப்பீர்கள். இது மைய விலக்கு விசை என்று அழைக்கப்படும். வட்டப்பாதையின் மையத்திலிருந்து ஒரு பொருளின் மீது வெளிப்புறமாகச் செயல்படும் விசையே மையவிலக்கு விசை எனப்படும். ஆகவே, மையவிலக்கு விசை, மையநோக்கு விசை செயல்படும் திசைக்கு எதிர்த்திசையில் செயல்படும். இதன் எண்மதிப்பு மையநோக்கு விசையின் எண் மதிப்பிற்குச் சமமாக இருக்கும். எடுத்துக்காட்டாக, துணி துவைக்கும் இயந்திரத்தில் உள்ள துணி உலர்த்தியில் மையவிலக்கு விசை செயல்படுகிறது.
பொழுதுபோக்கு பூங்காவில் குடை இராட்டினத்தில் சுற்றும்பொழுது நீங்கள் எந்த மாதிரியான விசையை உணர்கிறீர்கள்? குடை இராட்டினம் ஒரு செங்குத்து அச்சைப்பற்றி சுழலும்போது நாம் ஒரு வெளிநோக்கிய திசையில் ஏற்படும் இழுவிசையை உணர்கிறோம். இது மையவிலக்கு விசையினால் ஏற்படுவதாகும்.