அளவீட்டியல் Notes 7th Science Lesson 1 Notes in Tamil
7th Science Lesson 1 Notes in Tamil
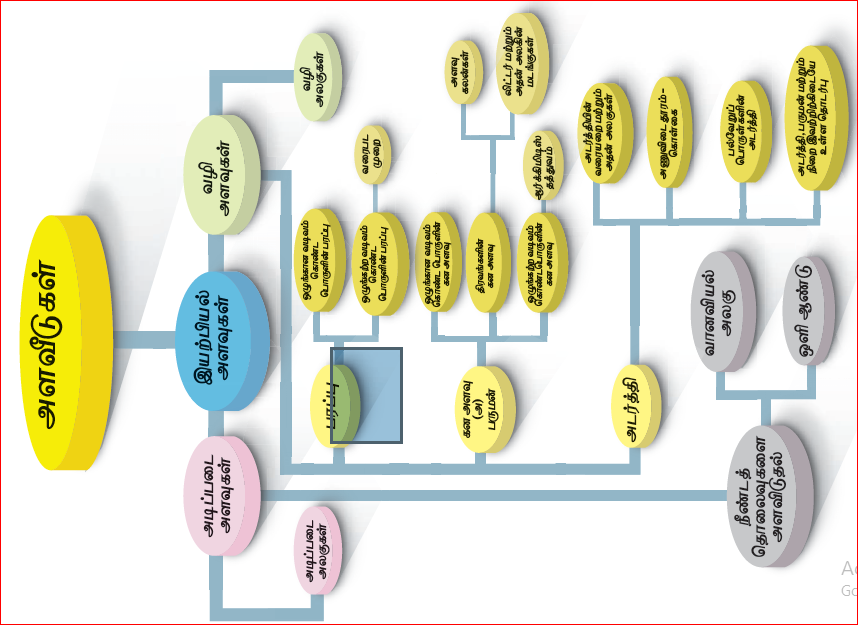
1] அளவீட்டியல்
அறிமுகம்:
| காய்கறிகள் | துணி | பால் | நேரம் |
| லிட்டர் | மீட்டர் | விநாடி | கிலோகிராம் |
நம் அன்றாட வாழ்வில் பழங்கள், காய்கறிகள், தானியங்கள் போன்றவற்றின் எடை, திரவங்களின் கனஅளவு, பொருளின் வெப்பநிலை, வாகனங்களின் வேகம் போன்ற பலவற்றினை அளவீடு செய்கிறோம். நிறை, எடை, தொலைவு, வெப்பநிலை, கனஅளவு போன்ற அளவுகள் இயற்பியல் அளவுகள் என அழைக்கப்படுகின்றன.
இயற்பியல் அளவுகளை அளந்தறிய எண் மதிப்புகளும், அலகுகளும் பயன்படுகின்றன. எடுத்துக்காட்டாக ஒரு நிகழ்வினை கருதுவோம்: சுரேஷ் தினந்தோறும் 2 கி.மீ நடைப்பயிற்சி மேற்கொள்கிறார். இந்நிகழ்வில் 2 என்பது எண் மதிப்பாகும். கி.மீ என்பது தொலைவு என்ற இயற்பியல் அளவின் மதிப்பினை குறிப்பதற்கு பயன்படும் அலகாகும்.
அடிப்படை மற்றும் வழி அளவுகள்:
பொதுவாக இயற்பியல் அளவுகள் இரண்டு வகைப்படும்.
- அடிப்படை அளவுகள்.
- வழி அளவுகள்.
அடிப்படை அளவுகள்:
வேறு எந்த இயற்பியல் அளவுகளாலும் குறிப்பிட இயலாத இயற்பியல் அளவுகள் அடிப்படை அளவுகள் எனப்படும். எ.கா:நீளம், நிறை, அடிப்படை அளவுகளை அளந்தறியப் பயன்படும் அலகுகள் அடிப்படை அலகுகள் எனப்படும். எ.கா:நீளத்தின் அலகு மீட்டர் ஆகும். SI அலகு முறையில் ஏழு அடிப்படை அளவுகள் உள்ளன. அடிப்படை அளவுகளும் அவற்றின் அலகுகளும் கீழே அட்டவணையில் கொடுக்கப்பட்டுள்ளன.
| வ. எண் |
அடிப்படை அளவுகள் | அடிப்படை அலகுகள் |
| நீளம் | மீட்டர் (மீ) (m) | |
| நிறை | கிலோகிராம் (கி.கி) (kg) | |
| நேரம் | வினாடி (வி) (s) | |
| வெப்பநிலை | கெல்வின் (K) | |
| மின்னோட்டம் | ஆம்பியர் (A) | |
| பொருளின் அளவு | மோல் (mol) | |
| ஓளிச்செறிவு | கேண்டிலா (cd) |
வழி அளவுகள்:
அடிப்படை அளவுகளைப் பெருக்கியோ அல்லது வகுத்தோ பெறப்படும் அளவுகள் வழி அளவுகள் எனப்படும். எ.கா: பரப்பு, கனஅளவு.
வழி அளவுகளை அளவிடப் பயன்படும் அலகுகள் வழி அலகுகள் எனப்படும். ஒரு சில வழி அளவுகளும் அவற்றின் அலகுகளும் கீழே உள்ள அட்டவணையில் தரப்பட்டுள்ளன.
சில வழி அளவுகளும் அவற்றின் அலகுகளும்
| வ.
எண் |
வழி அளவுகள் | வழி அலகுகள் |
| பரப்பு=நீளம்xஅகலம் | மீ x மீ = சதுர மீட்டர் (அ) மீ2 | |
| கனஅளவு (அ) பருமன்= நீளம்xஅகலம்xஉயரம் | மீ x மீx மீ = கனமீட்டர் (அ) மீ3 | |
| வேகம் = தூரம்/காலம் | மீ/வி (அ) மீவி-1 | |
| மின்னூட்டம் = மின்னோட்டம் x நேரம் | ஆம்பியர் வி (அ) கூலும் | |
| அடர்த்தி = நிறை /கனஅளவு | கிகி மீ3 (அ) கிகிமீ-3 |
பரப்பளவு:
பொருள் ஒன்றின் மேற்பரப்பின் அளவு அதன் பரப்பளவு எனப்படும்.
வீட்டு மனை ஒன்றின் பரப்பளவை காண அதன் நீளம் மற்றும் அகலத்தை பெருக்க வேண்டும்.
பரப்பளவு = நீளம் x அகலம்
பரப்பளவின் அலகு = மீட்டர் x மீட்டர்
= மீட்டர்2 அல்லது சதுர மீட்டர்
= மீ2 (இதனை சதுர மீட்டர் எனப்படிக்க வேண்டும்)
பரப்பளவு என்பது அடிப்படை அளவான நீளத்தினை இருமுறை பெருக்கிக் கணக்கிடப்படுவதால் பரப்பளவு வழி அளவாகும்.
கணக்கு 1.1.
ஒரு மீட்டர் பக்க அளவு கொண்ட 10 சதுரங்களை கொண்ட பொருளொன்றின் பரப்பளவு என்ன?
தீர்வு:
ஒரு சதுரத்தின் பரப்பளவு = பக்கம் x பக்கம்
= 1 மீ 1 மீ
= 1 மீ2
= 1 சதுர மீட்டர்
10 சதுரங்களை கொண்ட பொருளொன்றின் பரப்பளவு
= 1 சதுர மீட்டர் x 10
= 10 சதுர மீட்டர்
(பரப்பளவு என்பது சதுர மீட்டரில் குறிக்கப்பட்டாலும், பரப்பு சதுர வடிவமாக இருக்க வேண்டிய அவசியமில்லை)
ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவு ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பை தகுந்த சூத்திரங்களின் மூலம் கண்டறியலாம்.
ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பு
| வ.
எண் |
ஒழுங்கான வடிவம் | பொருளின் படம் | பரப்பு |
| சதுரம் | 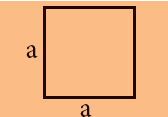 |
பக்கம் x பக்கம் = a x a = a2 | |
| செவ்வகம் | 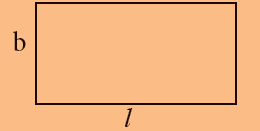 |
நீளம் x அகலம் = l x b = lb | |
| வட்டம் | 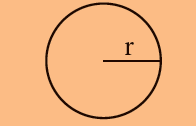 |
x r2 = x ஆரம்
x r x r r2 |
|
| முக்கோணம் |  |
(1/2) x அடிப்பக்கம் x உயரம்
½ x b x h ½ bh |
ஒரு சில ஒழுங்கான வடிவமுள்ள தள பொருள்களின் பரப்பைக் காண உதவும் சூத்திரங்கள் அட்டவணையில் தரப்பட்டுள்ளன.
கணக்கு 1.2:
கீழே தரப்பட்டுள்ள ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவைக் காணவும்: (ℼ = 22/7 எனக்கொள்க).
அ) 12 செ.மீ நீளமும் 4 செ.மீ அகலமும் கொண்ட செவ்வகம்.
ஆ) 7 செ.மீ ஆரம் கொண்ட வட்டம்.
இ) 6 செ.மீ அடிப்பக்கமும் 8 செ.மீ உயரமும் கொண்ட முக்கோணம்.
தீர்வு:
அ) செவ்வகத்தின் பரப்பு = நீளம் x அகலம் = 12 x 4 = 48 செ.மீ2
ஆ) வட்டத்தின் பரப்பு = ℼ x r2 = (22/7) x 7 x 7 = 154 செ.மீ2
இ) முக்கோணத்தின் பரப்பு = (1/2) x அடிx உயரம் = (1/2) x 6 x 8 = 24 செ.மீ2
ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவு:
நாம் நமது அன்றாட வாழ்வில் இலைகள், மலர்கள், மயில் இறகுகள் போன்ற பல ஒழுங்கற்ற வடிவமுள்ள பொருள்களைக் காண்கிறோம். இத்தகைய ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை நாம் சூத்திரத்தின் மூலம் காண இயலாது.
இத்தகைய பொருள்களின் பரப்பளவினை நாம் எவ்வாறு காணலாம்?
இது போன்ற ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை ஒரு வரைபடத் தாளைப் பயன்படுத்தி காணலாம்.
பின்வரும் செயல்பாடு ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை ஒரு வரைபடத்தாளைப் பயன்படுத்தி எவ்வாறு காணலாம் என விளக்குகிறது.
வரைபட முறையைக் கொண்டு, ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவினையும் காண முடியும். சதுர மற்றும் செவ்வக வடிவ பொருள்களின் பரப்பளவினை இம்முறையில் துல்லியமாகக் காண முடியும்.
கனஅளவு (அ) பருமன்:
ஒரு முப்பரிமாண பொருள் வெளியில் அல்லது சூழிடத்தில் ஆக்கிரமித்துக்கொள்ளும் இடமே அதன் கனஅளவு அல்லது பருமன் எனப்படும்.
கனஅளவு = அடிப்பரப்பு x உயரம்
கன அளவின் SI அலகு கன மீட்டர் (அ) மீ3 ஆகும்.
ஒழுங்கான வடிவமுள்ள பொருள்களின் கனஅளவு:
ஒழுங்கான வடிவமுள்ள பொருள்களின் கனஅளவினை அவற்றின் பரப்பளவைப் போலவே தகுந்த சூத்திரங்களின் மூலம் கண்டறியலாம். ஒரு சில ஒழுங்கான வடிவமுள்ள முப்பரிமாண பொருட்களின் கனஅளவினைக் காண உதவும் சூத்திரங்கள் தரப்பட்டுள்ளன.
கணக்கு 1.3:
அ) 3 செ.மீ பக்க அளவுள்ள கனசதுரம்.
ஆ) 3 மீ ஆரமும் 7 மீ உயரமும் கொண்ட உருளை ஆகியவற்றின் கனஅளவினைக் காணவும். ℼ = 22/7 எனக் கொள்ளவும்)
தீர்வு:
அ) கனசதுரத்தின் கனஅளவு
பக்கம் x பக்கம் x பக்கம் = 3 x 3 x 3 = 27 செ.மீ3 (அ) கன செ.மீ.
ஆ) உருளையின் கனஅளவு = ℼ x r2 x உயரம்
= (22/7) x 3 x 3 x 7 = 198 மீ3
திரவங்களின் கன அளவு:
திரவங்களும் வெளியில் அல்லது சூழிடத்தில் ஒரு குறிப்பிட்ட இடத்தை ஆக்கிரமித்துக்கொள்ளும். எனவே, திரவங்களும் ஒரு குறிப்பிட்ட பருமன் அல்லது கன அளவைக் கொண்டிருக்கும். ஆனால், திரவங்களுக்கு நிலையான வடிவம் கிடையாது. எனவே, திரவங்களின் கன அளவை திடப்பொருள்களுக்கு அளந்தது போல் அளக்க இயலாது. ஒரு திரவத்தை ஒரு கொள்கலனில் ஊற்றும்போது, திரவமானது கலனின் வடிவத்தையும் பருமனையும் பெறுகிறது. திரவத்தின் கள அளவு என்பது அது கலனில் எவ்வளவு இடத்தை நிரப்புகிறது என்பதே ஆகும். இதனை ஒரு அளவிடும் உருளை அல்லது அளவிடும் முகவை மூலம் அளக்கலாம். ஒரு கொள்கலனில் ஊற்றக்கூடிய அதிகபட்ச திரவத்தின் பருமனே கலனின்
ஒழுங்கான வடிவமுள்ள பொருள்களின் கனஅளவு
| வ.
எண் |
ஒழுங்கான வடிவம் | பொருளின் படம் | பருமன் |
| கனசதுரம் | 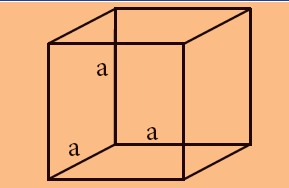 |
பக்கம் x பக்கம் x பக்கம்
a x a x a |
|
| கனசெவ்வகம் | 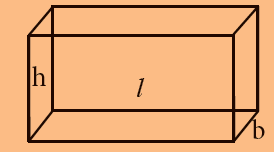 |
நீளம் x அகலம் x உயரம்
l x b x h |
|
| கோளம் | 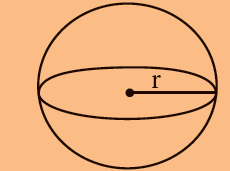 |
4/3 x ℼ x r3 (r என்பது ஆரம்) | |
| உருளை | 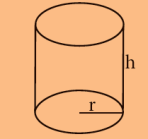 |
ℼ x r2 h ( h என்பது உயரம்) |
“கொள்ளளவு” எனப்படும். ஒரு அளவிடும் குவளையில் காட்டியுள்ளவாறு அளவீடுகள் வரையப்பட்டிருக்கும்.

அளவிடும் குவளை
திரவத்தின் கன அளவு என்பது அது கலனில் நிரப்பும் அளவைக் குறிக்கிறது என்பதே ஆகும். இதனை அளவிடும் குவளையில் வரையப்பட்டிருக்கும் அளவீடுகளிலிருந்து நேரடியாகக் குறிக்க இயலும். படத்தில் காட்டியுள்ள அளவிடும் குவளையை உற்று நோக்கும் போது, அதில் உள்ள அளவீடுகள் “ml” என்ற அலகில் குறிக்கப்பட்டுள்ளதை அறியலாம். இது மில்லி லிட்டர் என்பதைக் குறிக்கிறது. பருமனின் இந்த அலகினை புரிந்துக்கொள்ள, நாம் முதலில் லிட்டர் என்ற அலகைப் புரிந்துகொள்ள வேண்டும். ஏனெனில், லிட்டர் என்பது திரவங்களின் கனஅளவைக் குறிக்கப் பயன்படும் பொதுவான அலகாகும். ஒரு பொருளின் அளவை செ.மீ இல் குறிக்கும் போது, அதன் கனஅளவை கனசெ.மீ.இல் குறிக்க வேண்டும் என்பதை அறிவோம். இந்த கன செ.மீ என்ற அலகை பொதுவாக cc (cu-bic cm) எனக் குறிக்கிறோம் ஒரு லிட்டர் (l) என்பது 1000 cc ஆகும்.
1 லிட்டர் = 1000 cc அல்லது கன செ.மீ3 (cm3) 1000 மில்லி லிட்டர் (ml) = 1 லிட்டர்.
ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் கனஅளவு:
நாம் முன்பே விவாதித்தது போல், ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பருமனையும் சூத்திரங்களின் மூலம் காண இயலாது. இத்தகைய பொருள்களின் பருமனை ஒரு அளவிடும் குவளை மற்றும் நீரைக் கொண்டு அளக்கலாம்.
அடர்த்தி:
ஒரு முகவையில் நீரை எடுத்துக்கொண்டு, அதில் ஓர் இரும்புக் குண்டையும் ஒரு தக்கையையும் போடவும். நாம் காண்பது என்ன? இரும்புக் குண்டு மூழ்குகிறது; தக்கை மிதக்கிறது (படத்தில் காட்டியுள்ளபடி). இது ஏன் என விளக்கமுடியுமா? நமது பதில் “எடை மிகுந்த பொருள்கள் நீரில் மூழ்கும்; எடை குறைந்த பொருள்கள் நீரில் மிதக்கும்” எனில், எடை குறைந்த ஓர் உலோகக் காசு நீரில் மூழ்குவதும், எடை மிகுந்த மரக்கட்டை நீரில் மிதப்பதும் ஏன்? (படத்தில் காட்டியுள்ளபடி) நாம் அடர்த்தி பற்றிய கருத்துகளை புரிந்து கொண்டால், இக்கேள்விகளுக்கு சரியான பதில் அளிக்கலாம்.
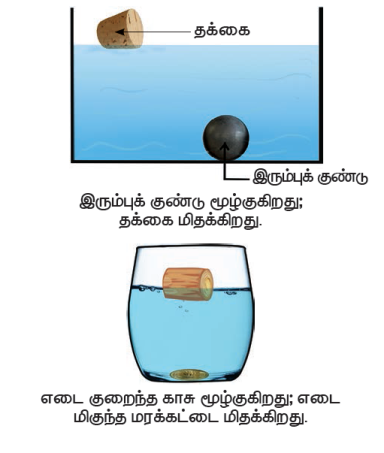
செயல்பாடு 4லிருந்து, மரத்துண்டு அதே நிறை கொண்ட இரும்புத் துண்டைவிட அதிக கனஅளவினைப் பெற்றுள்ளது என அறிகிறோம். மேலும், மரத்துண்டு அதே கனஅளவினைக் கொண்ட இரும்புத் துண்டைவிட குறைந்த நிறையைப் பெற்றுள்ளது எனவும் அறிகிறோம்.
பொருள் இலேசானதா அல்லது கனமானதா என்பதனைத் தீர்மானிக்கும் அளவு அடர்த்தி எனப்படும். சமமான கனஅளவு கொண்ட பொருள்களில் அதிக நிறை திணிக்கப்பட்டிருந்தால், அதன் அடர்த்தி அதிகம். எனவே இரும்புத்துண்டின் அடர்த்தி மரத்துண்டின் அடர்த்தியை விட அதிகமாகும்.
அடர்த்தியின் வரையறை:
ஒரு பொருளின் அடர்த்தி என்பது அதன் ஓரலகு பருமனில் (1 மீ3) அப்பொருள் பெற்றுள்ள நிறைக்குச் சமம் ஆகும்.
“m” நிறை கொண்ட ஒரு கொருளின் பருமன் “v” எனில், அதன் அடர்த்திக்கான சமன்பாடு:
அடர்த்தி (D) = நிறை (M) / பருமன்(V)
D = M/V
அடர்த்தியின் அலகு:
அடர்த்தியின் SI அலகு கிகி/மீ3. அதன் CGS அலகு கி/செ.மீ3
வெவ்வேறு பொருள்களின் அடர்த்தி:
வெவ்வேறு பொருள்கள் வெவ்வேறு அடர்த்தியைக் கொண்டிருக்கும். அதிக அடர்த்தியைக் கொண்ட பொருள்கள் “அடர்வான” அல்லது “அடர்வுமிகு” பொருள்கள் எனப்படும். குறைந்த அடர்த்தியைக் கொண்ட பொருள்கள் “தளர்வான” அல்லது “அடர்வுகுறை” பொருள்கள் எனப்படும்.
பெருமளவில் பயன்படும் சில பொருள்களின் அடர்த்தி, கீழ்காணும் அட்டவணையில் தரப்பட்டுள்ளன.
உன்னிடம் 1 கி.கி.நிறையுள்ள இரும்பு மற்றும் தங்கம் இருந்தால், அவற்றுள் எது அதிக பருமனைக் கொண்டிருக்கும்? உனது விடைக்கான காரணத்தைத் தருக.
கணக்கு 1.4:
280 கிகி நிறை கொண்ட ஒரு திட உருளையின் கனஅளவு 4 மீ3. அதன் அடர்த்தியைக் காண்க.
அட்டவணை: சில பொருள்களின் அடர்த்தி (அறை வெப்பநிலையில்)
| வ.எண் | இயல்பு | பொருள்கள் | அடர்த்தி (கிகி மீ3) |
| 1 | வாயு | காற்று | 1.2 |
| 2 | திரவம் | மண்ணெண்ணெய் | 800 |
| நீர் | 1,000 | ||
| பாதரசம் | 13,600 | ||
| 3 | திண்மம் | மரம் | 770 |
| அலுமினியம் | 2,700 | ||
| இரும்பு | 7,800 | ||
| தாமிரம் | 8,900 | ||
| வெள்ளி | 10,500 | ||
| தங்கம் | 19,300 |
தீர்வு:
உருளையின் அடர்த்தி (D) = உருளையின் நிறை (M) / உருளையின் கன அளவு (V)
= 280/4 = 70 கி.கி/மீ3
கணக்கு 1.5:
இரும்பினால் செய்யப்பட்ட ஒரு பெட்டியின் பருமன் 125 செ.மீ3. அதன் நிறையைக் காண்க. (இரும்பின் அடர்த்தி = 7.8 கி/செ.மீ3)
தீர்வு:
அடர்த்தி = நிறை/கனஅளவு
எனவே, நிறை = அடர்த்தி x கனஅளவு = 125 x 7.8 = 975 கி.
கணக்கு 1.6:
தாமிரத்தால் செய்யப்பட்ட ஒரு கோளத்தின் நிறை 3000 கி.கி. தாமிரத்தின் அடர்த்தி 8900 கி.கி/மீ3. எனில், கோளத்தின் பருமனைக் காண்க.
தீர்வு:
அடர்த்தி = நிறை/கனஅளவு
எனவே, கன அளவு = நிறை/அடர்த்தி = 3000/8900 = 0.34 மீ3
அடர்த்தி, நிறை, மற்றும் கன அளவு ஆகியவற்றுக்கிடையேயான தொடர்புகள் பின்வரும் அடர்த்தி முக்கோணத்தில் குறிக்கப்பட்டுள்ளன.
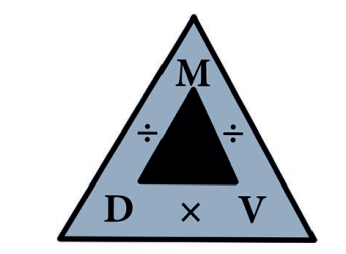
அடர்த்தி (D) = நிறை/கனஅளவு
நிறை (M) = அடர்த்தி x கனஅளவு
கனஅளவு (V) = நிறை/அடர்த்தி
அடர்த்தி, நிறை, மற்றும் கனஅளவு ஆகியவற்றுக்கிடையேயான தொடர்பு
வானியல் பொருள்களின் தொலைவினை அளத்தல்:
நாம் தினசரி வாழ்வில் அளவிடும் நீளங்களைக் குறிக்க சென்டிமீட்டர், மீட்டர் மற்றும் கிலோமீட்டர் போன்ற அலகுகளைப் பயன்படுத்துகிறோம். ஆனால், விண்வெளி ஆராய்ச்சியில், விண்வெளி ஆராய்ச்சியாளர்கள் பூமிக்கும் விண்மீனுக்கும் இடையில் உள்ள தொலைவு அல்லது இரு விண்மீன்களுக்கு இடையில் உள்ள தொலைவு போன்ற மிக நீண்ட தொலைவுகளை அளக்க வேண்டிய கட்டாயத்தில் உள்ளனர். இத்தகைய தொலைவுகளை அளவிட, கீழ்காணும் இரு அலகுகள் பயன்படுத்தப்படுகின்றன. அவை:
அ) வானியல் அலகு.
ஆ) ஒளி ஆண்டு.
வானியல் அலகு:
பூமியானது சூரியனை நீள்வட்டப்பாதையில் சுற்றுகிறது என்பது நாம் அறிந்ததே. எனவே, பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள தொலைவு ஒவ்வொரு நாளும் மாறிக்கொண்டே இருக்கும். பூமி அதன் அண்மை நிலையில் (அண்மை நிலை என்பது பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள தொலைவு மிகக்குறைவாக இருக்குபோது உள்ள நிலை) உள்ளபோது, பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள தொலைவு சுமார் 147.1 மில்லியன் கிலோமீட்டர் ஆகும். பூமியானது சூரியனிலிருந்து மிக அதிக தொலைவில் உள்ளபோது (இது சேய்மை நிலை என அழைக்கப்படும்), அவற்றிற்கிடையேயான தொலைவு சுமார் 152.1 மில்லியன் கிலோமீட்டர். (படத்தில் உள்ளவாறு) எனவே, பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள சராசரித் தொலைவு 149.6 மில்லியன் கிலோ மீட்டர் ஆகும். இத்தொலைவே “வானியல் அலகு” எனப்படுகிறது.
நெப்டியூன், சூரியனிலிருந்து 30 வானியல் அலகு தொலைவில் உள்ளது. அதாவது, நெப்டியூன் சூரியனிலிருந்து பூமி இருக்கும் தொலைவில் 30 மடங்கு தொலைவில் உள்ளது.
ஒரு வானியல் அலகு என்பது பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள சராசரித் தொலைவு ஆகும்.
1 வானியல் அலகு = 149.6 மில்லியன் கி.மீ = 149.6 x 106 கி.மீ = 1.496 x 1011 மீ.
ஓளி ஆண்டு:
நமது சூரிய குடும்பத்திற்கு மிக அருகில் அமைந்துள்ள விண்மீன் ப்ராகூமா சென்டாரி (Proxima Centauri). இதன் தொலைவு 2,68,770 வானியல் அலகாகும். இதிலிருந்து, விண்மீன்களின் தொலைவை வானியல் அலகால் குறிப்பிட்டால், அதை கையாள்வது கடினம் எனத்தெரிகிறது. எனவே, விண்வெளி ஆராய்ச்சியாளர்கள் இரு விண்மீன்களுக்கு இடையில் உள்ள தொலைவு போன்ற மிக நீண்ட தொலைவுகளை அளக்க “ஒளி ஆண்டு” என்னும் ஒரு தனித்தன்மை வாய்ந்த அலகினைப் பயன்படுத்துகின்றனர். வெற்றிடத்தில் ஒளியின் வேகம் 3 x 108 மீ/வி என்பதை நாம் அறிவோம். அதாவது, ஒளி ஒரு வினாடியில் 3 x 108 மீ தொலைவைக் கடக்கும். ஓர் ஆண்டில் (நெட்டாண்டு அல்லாத) 365 நாள்கள் உள்ளன. ஒரு நாளில் 24 மணி நேரமும், ஒரு மணி நேரத்தில் 60 நிமிடங்களும், ஒரு நிமிடத்தில் 60 வினாடிகளும் அடங்கியுள்ளன.
ஆகவே, ஓர் ஆண்டில்
உள்ள மொத்த வினாடிகளின் எண்ணிக்கை = 365 x 24 x 60 x 60
= 3.153 x 107 வினாடிகள்.
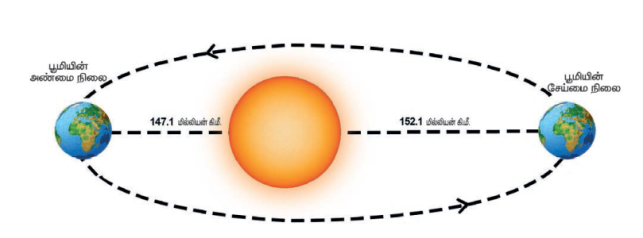
பூமியின் அண்மை மற்றும் சேய்மை நிலைகள்
ஒளியானது ஒரு வினாடியில் 3 x 108 மீ தொலைவைக் கடக்கும் எனில், ஓர் ஆண்டில் ஒளி கடக்கும் தொலைவு = 3 x 108 x 3.153 x 107 = 9.46 x 1015 மீ. இத்தொலைவே ஓர் ஒளி ஆண்டு எனப்படுகிறது.
ஒளி ஆண்டு என்பது ஒளியானது வெற்றிடத்தில் ஓர் ஆண்டில் கடக்கும் தொலைவே ஆகும்.
1 ஒளி ஆண்டு = 9.46 x 1015 மீ
ஓளி ஆண்டில் குறிக்கும்போது, ப்ராகூமா சென்டாரி (Proxima Centauri) நமது சூரிய குடும்பத்திலிருந்து (பூமியிலிருந்தும்) 4.22 ஒளி ஆண்டு தொலைவில் உள்ளது. பூமியானது அண்டத்தின் மையத்திலிருந்து 25,000 ஒளி ஆண்டு தொலைவில் உள்ளது.
நினைவில் கொள்க:
- வேறு எந்த இயற்பியல் அளவுகளாலும் குறிப்பிட இயலாத இயற்பியல் அளவுகள் அடிப்படை அளவுகள் எனப்படும். அவற்றிற்குரிய அலகுகள் அடிப்படை அலகுகள் எனப்படும்.
- அடிப்படை அளவுகளைப் பெருக்கியோ, அல்லது வகுத்தோ அளவுகள் வழி அளவுகள் எனப்படும். அவற்றிற்குரிய அலகுகள் வழி அலகுகள் எனப்படும்.
- ஒரு பொருளின் மேற்பரப்பே அதன் பரப்பளவு எனப்படும். இதன் SI அலகு சதுர மீட்டர் (அல்லது) மீ2 ஆகும்.
- ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பை ஒரு வரைபடத் தாளைப் பயன்படுத்தி காணலாம்.
- ஒரு முப்பரிமாண பொருள் வெளியில் அல்லது சூழிடத்தில் ஆக்கிரமித்துக் கொள்ளும் இடமே அப்பொருளின் கன அளவு அல்லது பருமன் எனப்படும். கன அளவின் SI அலகு கன மீட்டர் (அ) மீ3 ஆகும்.
- லிட்டர் என்பது திரவங்களின் கனஅளவைக் குறிக்கப் பயன்படும் பொதுவான ஓர் அலகாகும். ஒரு லிட்டர் = 1000 cc ஆகும்.
- ஒரு கொள்கலனில் ஊற்றக்கூடிய அதிகபட்ச திரவத்தின் பருமனே கலனின் “கொள்ளளவு” எனப்படும்.
- ஒரு பொருளின் அடர்த்தி என்பது அதன் ஓரலகு பருமனின் (1 மீ3) அப்பொருள் பெற்றுள்ள நிறை ஆகும்.
- அடர்த்தியின் SI அலகு கிகி/மீ3. அதன் CGS அலகு கி/செ.மீ3. 1 கி/செமீ3 = 103 கிகி/மீ3
- அதிக அடர்த்தியைக் கொண்ட பொருட்கள் “அடர்வான” அல்லது “அடர்வுமிகு” பொருள்கள் எனப்படும். குறைந்த அடர்த்தியைக் கொண்ட பொருள்கள் “தளர்வான” அல்லது “அடர்வுகுறை” பொருள்கள் எனப்படும்.
- ஒரு திடப்பொருளின் அடர்த்தி ஒரு திரவத்தின் அடர்த்தியை விட அதிகமானால், அது அத்திரவத்தில் மூழ்கும். ஒரு திடப்பொருளின் அடர்த்தி ஒரு திரவத்தின் அடர்த்தையை விட குறைவானால், அப்பொருள் அத்திரவத்தில் மிதக்கும்.
- அடர்த்தி = நிறை/கன அளவு.
- நிறை = அடர்த்தி x கனஅளவு.
- கன அளவு = நிறை/அடர்த்தி.
- ஒரு வானியல் அலகு என்பது பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள சராசரித் தொலைவு ஆகும். 1 வானியல் அலகு = 149.6 x 106 கி.மீ = 1.496 x 1011 மீ.
- ஓளி ஆண்டு என்பது ஒளியானது வெற்றிடத்தில் ஓர் ஆண்டில் கடக்கும் தொலைவே ஆகும். 1 ஒளி ஆண்டு = 9.46 x 1015 மீ.
உங்களுக்கு தெரியுமா?
- ஒரு சதுர மீட்டர் என்பது ஒரு மீட்டர் பக்க அளவு கொண்ட சதுரம் ஒன்றினுள் அடைப்படும் பரப்பாகும்.
- திரவங்களின் பருமனை அளக்க வேறு சில அலகுகளும் பயன்படுத்தப்படுகின்றன அவற்றுள் சில கேலன் (Gallon), அவுன்ஸ் (Ounce), மற்றும் குவார்ட் (Quart).
1 கேலன் = 3785 ml
1 அவுன்ஸ் = 30 ml
1 குவார்ட் = 1l
- சமையல் எண்ணெய் மற்றும் விளக்கெண்ணெய் போன்றவை பார்ப்பதற்கு நீரைவிட அடர்த்தி மிகுந்தவைகளாகத் தோற்றமளித்தாலும், அவற்றை விட நீர் அதிக அடர்த்தி கொண்டது. விளக்கெண்ணெயின் அடர்த்தி 961 கி.கி / மீ3. விளக்கெண்ணெய்யில் ஒரு துளி நீரை இடும்பொழுது, நீர்த்துளி மூழ்கும். ஆனால், நீரில் ஒரு துளி விளக்கெண்ணெய்யை இடும்பொழுது, அது மிதந்து நீரின் மீது ஒரு படலத்தை உருவாகும். எனினும், சில எண்ணெய் வகைகள் நீரை விட அதிக அடர்த்தி கொண்டவை.
7th Science Lesson 1 Notes in Tamil
1] அளவீட்டியல்
அறிமுகம்:
| காய்கறிகள் | துணி | பால் | நேரம் |
| லிட்டர் | மீட்டர் | விநாடி | கிலோகிராம் |
நம் அன்றாட வாழ்வில் பழங்கள், காய்கறிகள், தானியங்கள் போன்றவற்றின் எடை, திரவங்களின் கனஅளவு, பொருளின் வெப்பநிலை, வாகனங்களின் வேகம் போன்ற பலவற்றினை அளவீடு செய்கிறோம். நிறை, எடை, தொலைவு, வெப்பநிலை, கனஅளவு போன்ற அளவுகள் இயற்பியல் அளவுகள் என அழைக்கப்படுகின்றன.
இயற்பியல் அளவுகளை அளந்தறிய எண் மதிப்புகளும், அலகுகளும் பயன்படுகின்றன. எடுத்துக்காட்டாக ஒரு நிகழ்வினை கருதுவோம்: சுரேஷ் தினந்தோறும் 2 கி.மீ நடைப்பயிற்சி மேற்கொள்கிறார். இந்நிகழ்வில் 2 என்பது எண் மதிப்பாகும். கி.மீ என்பது தொலைவு என்ற இயற்பியல் அளவின் மதிப்பினை குறிப்பதற்கு பயன்படும் அலகாகும்.
அடிப்படை மற்றும் வழி அளவுகள்:
பொதுவாக இயற்பியல் அளவுகள் இரண்டு வகைப்படும்.
- அடிப்படை அளவுகள்.
- வழி அளவுகள்.
அடிப்படை அளவுகள்:
வேறு எந்த இயற்பியல் அளவுகளாலும் குறிப்பிட இயலாத இயற்பியல் அளவுகள் அடிப்படை அளவுகள் எனப்படும். எ.கா:நீளம், நிறை, அடிப்படை அளவுகளை அளந்தறியப் பயன்படும் அலகுகள் அடிப்படை அலகுகள் எனப்படும். எ.கா:நீளத்தின் அலகு மீட்டர் ஆகும். SI அலகு முறையில் ஏழு அடிப்படை அளவுகள் உள்ளன. அடிப்படை அளவுகளும் அவற்றின் அலகுகளும் கீழே அட்டவணையில் கொடுக்கப்பட்டுள்ளன.
| வ.
எண் |
அடிப்படை அளவுகள் | அடிப்படை அலகுகள் |
| நீளம் | மீட்டர் (மீ) (m) | |
| நிறை | கிலோகிராம் (கி.கி) (kg) | |
| நேரம் | வினாடி (வி) (s) | |
| வெப்பநிலை | கெல்வின் (K) | |
| மின்னோட்டம் | ஆம்பியர் (A) | |
| பொருளின் அளவு | மோல் (mol) | |
| ஓளிச்செறிவு | கேண்டிலா (cd) |
வழி அளவுகள்:
அடிப்படை அளவுகளைப் பெருக்கியோ அல்லது வகுத்தோ பெறப்படும் அளவுகள் வழி அளவுகள் எனப்படும். எ.கா: பரப்பு, கனஅளவு.
வழி அளவுகளை அளவிடப் பயன்படும் அலகுகள் வழி அலகுகள் எனப்படும். ஒரு சில வழி அளவுகளும் அவற்றின் அலகுகளும் கீழே உள்ள அட்டவணையில் தரப்பட்டுள்ளன.
சில வழி அளவுகளும் அவற்றின் அலகுகளும்
| வ.
எண் |
வழி அளவுகள் | வழி அலகுகள் |
| பரப்பு=நீளம்xஅகலம் | மீ x மீ = சதுர மீட்டர் (அ) மீ2 | |
| கனஅளவு (அ) பருமன்= நீளம்xஅகலம்xஉயரம் | மீ x மீx மீ = கனமீட்டர் (அ) மீ3 | |
| வேகம் = தூரம்/காலம் | மீ/வி (அ) மீவி-1 | |
| மின்னூட்டம் = மின்னோட்டம் x நேரம் | ஆம்பியர் வி (அ) கூலும் | |
| அடர்த்தி = நிறை /கனஅளவு | கிகி மீ3 (அ) கிகிமீ-3 |

பரப்பளவு:
பொருள் ஒன்றின் மேற்பரப்பின் அளவு அதன் பரப்பளவு எனப்படும்.
வீட்டு மனை ஒன்றின் பரப்பளவை காண அதன் நீளம் மற்றும் அகலத்தை பெருக்க வேண்டும்.
பரப்பளவு = நீளம் x அகலம்
பரப்பளவின் அலகு = மீட்டர் x மீட்டர்
= மீட்டர்2 அல்லது சதுர மீட்டர்
= மீ2 (இதனை சதுர மீட்டர் எனப்படிக்க வேண்டும்)
பரப்பளவு என்பது அடிப்படை அளவான நீளத்தினை இருமுறை பெருக்கிக் கணக்கிடப்படுவதால் பரப்பளவு வழி அளவாகும்.
கணக்கு 1.1.
ஒரு மீட்டர் பக்க அளவு கொண்ட 10 சதுரங்களை கொண்ட பொருளொன்றின் பரப்பளவு என்ன?
தீர்வு:
ஒரு சதுரத்தின் பரப்பளவு = பக்கம் x பக்கம்
= 1 மீ 1 மீ
= 1 மீ2
= 1 சதுர மீட்டர்
10 சதுரங்களை கொண்ட பொருளொன்றின் பரப்பளவு
= 1 சதுர மீட்டர் x 10
= 10 சதுர மீட்டர்
(பரப்பளவு என்பது சதுர மீட்டரில் குறிக்கப்பட்டாலும், பரப்பு சதுர வடிவமாக இருக்க வேண்டிய அவசியமில்லை)
ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவு ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பை தகுந்த சூத்திரங்களின் மூலம் கண்டறியலாம்.
ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பு
| வ.
எண் |
ஒழுங்கான வடிவம் | பொருளின் படம் | பரப்பு |
| சதுரம் |  |
பக்கம் x பக்கம் = a x a = a2 | |
| செவ்வகம் |  |
நீளம் x அகலம் = l x b = lb | |
| வட்டம் | 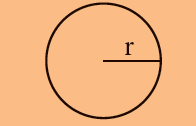 |
x r2 = x ஆரம்
x r x r r2 |
|
| முக்கோணம் |  |
(1/2) x அடிப்பக்கம் x உயரம்
½ x b x h ½ bh |
ஒரு சில ஒழுங்கான வடிவமுள்ள தள பொருள்களின் பரப்பைக் காண உதவும் சூத்திரங்கள் அட்டவணையில் தரப்பட்டுள்ளன.
கணக்கு 1.2:
கீழே தரப்பட்டுள்ள ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவைக் காணவும்: (ℼ = 22/7 எனக்கொள்க).
அ) 12 செ.மீ நீளமும் 4 செ.மீ அகலமும் கொண்ட செவ்வகம்.
ஆ) 7 செ.மீ ஆரம் கொண்ட வட்டம்.
இ) 6 செ.மீ அடிப்பக்கமும் 8 செ.மீ உயரமும் கொண்ட முக்கோணம்.
தீர்வு:
அ) செவ்வகத்தின் பரப்பு = நீளம் x அகலம் = 12 x 4 = 48 செ.மீ2
ஆ) வட்டத்தின் பரப்பு = ℼ x r2 = (22/7) x 7 x 7 = 154 செ.மீ2
இ) முக்கோணத்தின் பரப்பு = (1/2) x அடிx உயரம் = (1/2) x 6 x 8 = 24 செ.மீ2
ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவு:
நாம் நமது அன்றாட வாழ்வில் இலைகள், மலர்கள், மயில் இறகுகள் போன்ற பல ஒழுங்கற்ற வடிவமுள்ள பொருள்களைக் காண்கிறோம். இத்தகைய ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை நாம் சூத்திரத்தின் மூலம் காண இயலாது.
இத்தகைய பொருள்களின் பரப்பளவினை நாம் எவ்வாறு காணலாம்?
இது போன்ற ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை ஒரு வரைபடத் தாளைப் பயன்படுத்தி காணலாம்.
பின்வரும் செயல்பாடு ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை ஒரு வரைபடத்தாளைப் பயன்படுத்தி எவ்வாறு காணலாம் என விளக்குகிறது.
வரைபட முறையைக் கொண்டு, ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவினையும் காண முடியும். சதுர மற்றும் செவ்வக வடிவ பொருள்களின் பரப்பளவினை இம்முறையில் துல்லியமாகக் காண முடியும்.
கனஅளவு (அ) பருமன்:
ஒரு முப்பரிமாண பொருள் வெளியில் அல்லது சூழிடத்தில் ஆக்கிரமித்துக்கொள்ளும் இடமே அதன் கனஅளவு அல்லது பருமன் எனப்படும்.
கனஅளவு = அடிப்பரப்பு x உயரம்
கன அளவின் SI அலகு கன மீட்டர் (அ) மீ3 ஆகும்.
ஒழுங்கான வடிவமுள்ள பொருள்களின் கனஅளவு:
ஒழுங்கான வடிவமுள்ள பொருள்களின் கனஅளவினை அவற்றின் பரப்பளவைப் போலவே தகுந்த சூத்திரங்களின் மூலம் கண்டறியலாம். ஒரு சில ஒழுங்கான வடிவமுள்ள முப்பரிமாண பொருட்களின் கனஅளவினைக் காண உதவும் சூத்திரங்கள் தரப்பட்டுள்ளன.
கணக்கு 1.3:
அ) 3 செ.மீ பக்க அளவுள்ள கனசதுரம்.
ஆ) 3 மீ ஆரமும் 7 மீ உயரமும் கொண்ட உருளை ஆகியவற்றின் கனஅளவினைக் காணவும். ℼ = 22/7 எனக் கொள்ளவும்)
தீர்வு:
அ) கனசதுரத்தின் கனஅளவு
பக்கம் x பக்கம் x பக்கம் = 3 x 3 x 3 = 27 செ.மீ3 (அ) கன செ.மீ.
ஆ) உருளையின் கனஅளவு = ℼ x r2 x உயரம்
= (22/7) x 3 x 3 x 7 = 198 மீ3
திரவங்களின் கன அளவு:
திரவங்களும் வெளியில் அல்லது சூழிடத்தில் ஒரு குறிப்பிட்ட இடத்தை ஆக்கிரமித்துக்கொள்ளும். எனவே, திரவங்களும் ஒரு குறிப்பிட்ட பருமன் அல்லது கன அளவைக் கொண்டிருக்கும். ஆனால், திரவங்களுக்கு நிலையான வடிவம் கிடையாது. எனவே, திரவங்களின் கன அளவை திடப்பொருள்களுக்கு அளந்தது போல் அளக்க இயலாது. ஒரு திரவத்தை ஒரு கொள்கலனில் ஊற்றும்போது, திரவமானது கலனின் வடிவத்தையும் பருமனையும் பெறுகிறது. திரவத்தின் கள அளவு என்பது அது கலனில் எவ்வளவு இடத்தை நிரப்புகிறது என்பதே ஆகும். இதனை ஒரு அளவிடும் உருளை அல்லது அளவிடும் முகவை மூலம் அளக்கலாம். ஒரு கொள்கலனில் ஊற்றக்கூடிய அதிகபட்ச திரவத்தின் பருமனே கலனின்
ஒழுங்கான வடிவமுள்ள பொருள்களின் கனஅளவு
| வ.
எண் |
ஒழுங்கான வடிவம் | பொருளின் படம் | பருமன் |
| கனசதுரம் | 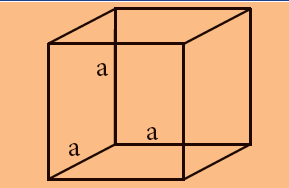 |
பக்கம் x பக்கம் x பக்கம்
a x a x a |
|
| கனசெவ்வகம் |  |
நீளம் x அகலம் x உயரம்
l x b x h |
|
| கோளம் |  |
4/3 x ℼ x r3 (r என்பது ஆரம்) | |
| உருளை |  |
ℼ x r2 h ( h என்பது உயரம்) |
“கொள்ளளவு” எனப்படும். ஒரு அளவிடும் குவளையில் காட்டியுள்ளவாறு அளவீடுகள் வரையப்பட்டிருக்கும்.

அளவிடும் குவளை
திரவத்தின் கன அளவு என்பது அது கலனில் நிரப்பும் அளவைக் குறிக்கிறது என்பதே ஆகும். இதனை அளவிடும் குவளையில் வரையப்பட்டிருக்கும் அளவீடுகளிலிருந்து நேரடியாகக் குறிக்க இயலும். படத்தில் காட்டியுள்ள அளவிடும் குவளையை உற்று நோக்கும் போது, அதில் உள்ள அளவீடுகள் “ml” என்ற அலகில் குறிக்கப்பட்டுள்ளதை அறியலாம். இது மில்லி லிட்டர் என்பதைக் குறிக்கிறது. பருமனின் இந்த அலகினை புரிந்துக்கொள்ள, நாம் முதலில் லிட்டர் என்ற அலகைப் புரிந்துகொள்ள வேண்டும். ஏனெனில், லிட்டர் என்பது திரவங்களின் கனஅளவைக் குறிக்கப் பயன்படும் பொதுவான அலகாகும். ஒரு பொருளின் அளவை செ.மீ இல் குறிக்கும் போது, அதன் கனஅளவை கனசெ.மீ.இல் குறிக்க வேண்டும் என்பதை அறிவோம். இந்த கன செ.மீ என்ற அலகை பொதுவாக cc (cu-bic cm) எனக் குறிக்கிறோம் ஒரு லிட்டர் (l) என்பது 1000 cc ஆகும்.
1 லிட்டர் = 1000 cc அல்லது கன செ.மீ3 (cm3) 1000 மில்லி லிட்டர் (ml) = 1 லிட்டர்.
ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் கனஅளவு:
நாம் முன்பே விவாதித்தது போல், ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பருமனையும் சூத்திரங்களின் மூலம் காண இயலாது. இத்தகைய பொருள்களின் பருமனை ஒரு அளவிடும் குவளை மற்றும் நீரைக் கொண்டு அளக்கலாம்.
அடர்த்தி:
ஒரு முகவையில் நீரை எடுத்துக்கொண்டு, அதில் ஓர் இரும்புக் குண்டையும் ஒரு தக்கையையும் போடவும். நாம் காண்பது என்ன? இரும்புக் குண்டு மூழ்குகிறது; தக்கை மிதக்கிறது (படத்தில் காட்டியுள்ளபடி). இது ஏன் என விளக்கமுடியுமா? நமது பதில் “எடை மிகுந்த பொருள்கள் நீரில் மூழ்கும்; எடை குறைந்த பொருள்கள் நீரில் மிதக்கும்” எனில், எடை குறைந்த ஓர் உலோகக் காசு நீரில் மூழ்குவதும், எடை மிகுந்த மரக்கட்டை நீரில் மிதப்பதும் ஏன்? (படத்தில் காட்டியுள்ளபடி) நாம் அடர்த்தி பற்றிய கருத்துகளை புரிந்து கொண்டால், இக்கேள்விகளுக்கு சரியான பதில் அளிக்கலாம்.

செயல்பாடு 4லிருந்து, மரத்துண்டு அதே நிறை கொண்ட இரும்புத் துண்டைவிட அதிக கனஅளவினைப் பெற்றுள்ளது என அறிகிறோம். மேலும், மரத்துண்டு அதே கனஅளவினைக் கொண்ட இரும்புத் துண்டைவிட குறைந்த நிறையைப் பெற்றுள்ளது எனவும் அறிகிறோம்.
பொருள் இலேசானதா அல்லது கனமானதா என்பதனைத் தீர்மானிக்கும் அளவு அடர்த்தி எனப்படும். சமமான கனஅளவு கொண்ட பொருள்களில் அதிக நிறை திணிக்கப்பட்டிருந்தால், அதன் அடர்த்தி அதிகம். எனவே இரும்புத்துண்டின் அடர்த்தி மரத்துண்டின் அடர்த்தியை விட அதிகமாகும்.
அடர்த்தியின் வரையறை:
ஒரு பொருளின் அடர்த்தி என்பது அதன் ஓரலகு பருமனில் (1 மீ3) அப்பொருள் பெற்றுள்ள நிறைக்குச் சமம் ஆகும்.
“m” நிறை கொண்ட ஒரு கொருளின் பருமன் “v” எனில், அதன் அடர்த்திக்கான சமன்பாடு:
அடர்த்தி (D) = நிறை (M) / பருமன்(V)
D = M/V
அடர்த்தியின் அலகு:
அடர்த்தியின் SI அலகு கிகி/மீ3. அதன் CGS அலகு கி/செ.மீ3
வெவ்வேறு பொருள்களின் அடர்த்தி:
வெவ்வேறு பொருள்கள் வெவ்வேறு அடர்த்தியைக் கொண்டிருக்கும். அதிக அடர்த்தியைக் கொண்ட பொருள்கள் “அடர்வான” அல்லது “அடர்வுமிகு” பொருள்கள் எனப்படும். குறைந்த அடர்த்தியைக் கொண்ட பொருள்கள் “தளர்வான” அல்லது “அடர்வுகுறை” பொருள்கள் எனப்படும்.
பெருமளவில் பயன்படும் சில பொருள்களின் அடர்த்தி, கீழ்காணும் அட்டவணையில் தரப்பட்டுள்ளன.
உன்னிடம் 1 கி.கி.நிறையுள்ள இரும்பு மற்றும் தங்கம் இருந்தால், அவற்றுள் எது அதிக பருமனைக் கொண்டிருக்கும்? உனது விடைக்கான காரணத்தைத் தருக.
கணக்கு 1.4:
280 கிகி நிறை கொண்ட ஒரு திட உருளையின் கனஅளவு 4 மீ3. அதன் அடர்த்தியைக் காண்க.
அட்டவணை: சில பொருள்களின் அடர்த்தி (அறை வெப்பநிலையில்)
| வ.எண் | இயல்பு | பொருள்கள் | அடர்த்தி (கிகி மீ3) |
| 1 | வாயு | காற்று | 1.2 |
| 2 | திரவம் | மண்ணெண்ணெய் | 800 |
| நீர் | 1,000 | ||
| பாதரசம் | 13,600 | ||
| 3 | திண்மம் | மரம் | 770 |
| அலுமினியம் | 2,700 | ||
| இரும்பு | 7,800 | ||
| தாமிரம் | 8,900 | ||
| வெள்ளி | 10,500 | ||
| தங்கம் | 19,300 |
தீர்வு:
உருளையின் அடர்த்தி (D) = உருளையின் நிறை (M) / உருளையின் கன அளவு (V)
= 280/4 = 70 கி.கி/மீ3
கணக்கு 1.5:
இரும்பினால் செய்யப்பட்ட ஒரு பெட்டியின் பருமன் 125 செ.மீ3. அதன் நிறையைக் காண்க. (இரும்பின் அடர்த்தி = 7.8 கி/செ.மீ3)
தீர்வு:
அடர்த்தி = நிறை/கனஅளவு
எனவே, நிறை = அடர்த்தி x கனஅளவு = 125 x 7.8 = 975 கி.
கணக்கு 1.6:
தாமிரத்தால் செய்யப்பட்ட ஒரு கோளத்தின் நிறை 3000 கி.கி. தாமிரத்தின் அடர்த்தி 8900 கி.கி/மீ3. எனில், கோளத்தின் பருமனைக் காண்க.
தீர்வு:
அடர்த்தி = நிறை/கனஅளவு
எனவே, கன அளவு = நிறை/அடர்த்தி = 3000/8900 = 0.34 மீ3
அடர்த்தி, நிறை, மற்றும் கன அளவு ஆகியவற்றுக்கிடையேயான தொடர்புகள் பின்வரும் அடர்த்தி முக்கோணத்தில் குறிக்கப்பட்டுள்ளன.
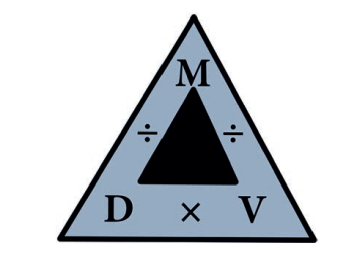
அடர்த்தி (D) = நிறை/கனஅளவு
நிறை (M) = அடர்த்தி x கனஅளவு
கனஅளவு (V) = நிறை/அடர்த்தி
அடர்த்தி, நிறை, மற்றும் கனஅளவு ஆகியவற்றுக்கிடையேயான தொடர்பு
வானியல் பொருள்களின் தொலைவினை அளத்தல்:
நாம் தினசரி வாழ்வில் அளவிடும் நீளங்களைக் குறிக்க சென்டிமீட்டர், மீட்டர் மற்றும் கிலோமீட்டர் போன்ற அலகுகளைப் பயன்படுத்துகிறோம். ஆனால், விண்வெளி ஆராய்ச்சியில், விண்வெளி ஆராய்ச்சியாளர்கள் பூமிக்கும் விண்மீனுக்கும் இடையில் உள்ள தொலைவு அல்லது இரு விண்மீன்களுக்கு இடையில் உள்ள தொலைவு போன்ற மிக நீண்ட தொலைவுகளை அளக்க வேண்டிய கட்டாயத்தில் உள்ளனர். இத்தகைய தொலைவுகளை அளவிட, கீழ்காணும் இரு அலகுகள் பயன்படுத்தப்படுகின்றன. அவை:
அ) வானியல் அலகு.
ஆ) ஒளி ஆண்டு.
வானியல் அலகு:
பூமியானது சூரியனை நீள்வட்டப்பாதையில் சுற்றுகிறது என்பது நாம் அறிந்ததே. எனவே, பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள தொலைவு ஒவ்வொரு நாளும் மாறிக்கொண்டே இருக்கும். பூமி அதன் அண்மை நிலையில் (அண்மை நிலை என்பது பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள தொலைவு மிகக்குறைவாக இருக்குபோது உள்ள நிலை) உள்ளபோது, பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள தொலைவு சுமார் 147.1 மில்லியன் கிலோமீட்டர் ஆகும். பூமியானது சூரியனிலிருந்து மிக அதிக தொலைவில் உள்ளபோது (இது சேய்மை நிலை என அழைக்கப்படும்), அவற்றிற்கிடையேயான தொலைவு சுமார் 152.1 மில்லியன் கிலோமீட்டர். (படத்தில் உள்ளவாறு) எனவே, பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள சராசரித் தொலைவு 149.6 மில்லியன் கிலோ மீட்டர் ஆகும். இத்தொலைவே “வானியல் அலகு” எனப்படுகிறது.
நெப்டியூன், சூரியனிலிருந்து 30 வானியல் அலகு தொலைவில் உள்ளது. அதாவது, நெப்டியூன் சூரியனிலிருந்து பூமி இருக்கும் தொலைவில் 30 மடங்கு தொலைவில் உள்ளது.
ஒரு வானியல் அலகு என்பது பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள சராசரித் தொலைவு ஆகும்.
1 வானியல் அலகு = 149.6 மில்லியன் கி.மீ = 149.6 x 106 கி.மீ = 1.496 x 1011 மீ.
ஓளி ஆண்டு:
நமது சூரிய குடும்பத்திற்கு மிக அருகில் அமைந்துள்ள விண்மீன் ப்ராகூமா சென்டாரி (Proxima Centauri). இதன் தொலைவு 2,68,770 வானியல் அலகாகும். இதிலிருந்து, விண்மீன்களின் தொலைவை வானியல் அலகால் குறிப்பிட்டால், அதை கையாள்வது கடினம் எனத்தெரிகிறது. எனவே, விண்வெளி ஆராய்ச்சியாளர்கள் இரு விண்மீன்களுக்கு இடையில் உள்ள தொலைவு போன்ற மிக நீண்ட தொலைவுகளை அளக்க “ஒளி ஆண்டு” என்னும் ஒரு தனித்தன்மை வாய்ந்த அலகினைப் பயன்படுத்துகின்றனர். வெற்றிடத்தில் ஒளியின் வேகம் 3 x 108 மீ/வி என்பதை நாம் அறிவோம். அதாவது, ஒளி ஒரு வினாடியில் 3 x 108 மீ தொலைவைக் கடக்கும். ஓர் ஆண்டில் (நெட்டாண்டு அல்லாத) 365 நாள்கள் உள்ளன. ஒரு நாளில் 24 மணி நேரமும், ஒரு மணி நேரத்தில் 60 நிமிடங்களும், ஒரு நிமிடத்தில் 60 வினாடிகளும் அடங்கியுள்ளன.
ஆகவே, ஓர் ஆண்டில்
உள்ள மொத்த வினாடிகளின் எண்ணிக்கை = 365 x 24 x 60 x 60
= 3.153 x 107 வினாடிகள்.
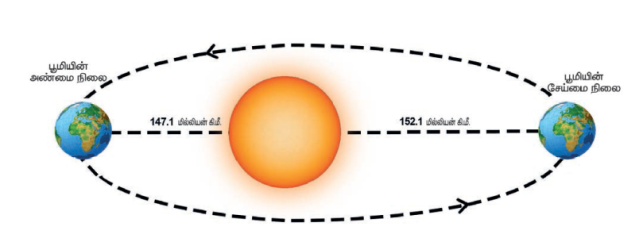
பூமியின் அண்மை மற்றும் சேய்மை நிலைகள்
ஒளியானது ஒரு வினாடியில் 3 x 108 மீ தொலைவைக் கடக்கும் எனில், ஓர் ஆண்டில் ஒளி கடக்கும் தொலைவு = 3 x 108 x 3.153 x 107 = 9.46 x 1015 மீ. இத்தொலைவே ஓர் ஒளி ஆண்டு எனப்படுகிறது.
ஒளி ஆண்டு என்பது ஒளியானது வெற்றிடத்தில் ஓர் ஆண்டில் கடக்கும் தொலைவே ஆகும்.
1 ஒளி ஆண்டு = 9.46 x 1015 மீ
ஓளி ஆண்டில் குறிக்கும்போது, ப்ராகூமா சென்டாரி (Proxima Centauri) நமது சூரிய குடும்பத்திலிருந்து (பூமியிலிருந்தும்) 4.22 ஒளி ஆண்டு தொலைவில் உள்ளது. பூமியானது அண்டத்தின் மையத்திலிருந்து 25,000 ஒளி ஆண்டு தொலைவில் உள்ளது.
நினைவில் கொள்க:
- வேறு எந்த இயற்பியல் அளவுகளாலும் குறிப்பிட இயலாத இயற்பியல் அளவுகள் அடிப்படை அளவுகள் எனப்படும். அவற்றிற்குரிய அலகுகள் அடிப்படை அலகுகள் எனப்படும்.
- அடிப்படை அளவுகளைப் பெருக்கியோ, அல்லது வகுத்தோ அளவுகள் வழி அளவுகள் எனப்படும். அவற்றிற்குரிய அலகுகள் வழி அலகுகள் எனப்படும்.
- ஒரு பொருளின் மேற்பரப்பே அதன் பரப்பளவு எனப்படும். இதன் SI அலகு சதுர மீட்டர் (அல்லது) மீ2 ஆகும்.
- ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பை ஒரு வரைபடத் தாளைப் பயன்படுத்தி காணலாம்.
- ஒரு முப்பரிமாண பொருள் வெளியில் அல்லது சூழிடத்தில் ஆக்கிரமித்துக் கொள்ளும் இடமே அப்பொருளின் கன அளவு அல்லது பருமன் எனப்படும். கன அளவின் SI அலகு கன மீட்டர் (அ) மீ3 ஆகும்.
- லிட்டர் என்பது திரவங்களின் கனஅளவைக் குறிக்கப் பயன்படும் பொதுவான ஓர் அலகாகும். ஒரு லிட்டர் = 1000 cc ஆகும்.
- ஒரு கொள்கலனில் ஊற்றக்கூடிய அதிகபட்ச திரவத்தின் பருமனே கலனின் “கொள்ளளவு” எனப்படும்.
- ஒரு பொருளின் அடர்த்தி என்பது அதன் ஓரலகு பருமனின் (1 மீ3) அப்பொருள் பெற்றுள்ள நிறை ஆகும்.
- அடர்த்தியின் SI அலகு கிகி/மீ3. அதன் CGS அலகு கி/செ.மீ3. 1 கி/செமீ3 = 103 கிகி/மீ3
- அதிக அடர்த்தியைக் கொண்ட பொருட்கள் “அடர்வான” அல்லது “அடர்வுமிகு” பொருள்கள் எனப்படும். குறைந்த அடர்த்தியைக் கொண்ட பொருள்கள் “தளர்வான” அல்லது “அடர்வுகுறை” பொருள்கள் எனப்படும்.
- ஒரு திடப்பொருளின் அடர்த்தி ஒரு திரவத்தின் அடர்த்தியை விட அதிகமானால், அது அத்திரவத்தில் மூழ்கும். ஒரு திடப்பொருளின் அடர்த்தி ஒரு திரவத்தின் அடர்த்தையை விட குறைவானால், அப்பொருள் அத்திரவத்தில் மிதக்கும்.
- அடர்த்தி = நிறை/கன அளவு.
- நிறை = அடர்த்தி x கனஅளவு.
- கன அளவு = நிறை/அடர்த்தி.
- ஒரு வானியல் அலகு என்பது பூமிக்கும் சூரியனுக்கும் இடையேயுள்ள சராசரித் தொலைவு ஆகும். 1 வானியல் அலகு = 149.6 x 106 கி.மீ = 1.496 x 1011 மீ.
- ஓளி ஆண்டு என்பது ஒளியானது வெற்றிடத்தில் ஓர் ஆண்டில் கடக்கும் தொலைவே ஆகும். 1 ஒளி ஆண்டு = 9.46 x 1015 மீ.
உங்களுக்கு தெரியுமா?
- ஒரு சதுர மீட்டர் என்பது ஒரு மீட்டர் பக்க அளவு கொண்ட சதுரம் ஒன்றினுள் அடைப்படும் பரப்பாகும்.
- திரவங்களின் பருமனை அளக்க வேறு சில அலகுகளும் பயன்படுத்தப்படுகின்றன அவற்றுள் சில கேலன் (Gallon), அவுன்ஸ் (Ounce), மற்றும் குவார்ட் (Quart).
1 கேலன் = 3785 ml
1 அவுன்ஸ் = 30 ml
1 குவார்ட் = 1l
- சமையல் எண்ணெய் மற்றும் விளக்கெண்ணெய் போன்றவை பார்ப்பதற்கு நீரைவிட அடர்த்தி மிகுந்தவைகளாகத் தோற்றமளித்தாலும், அவற்றை விட நீர் அதிக அடர்த்தி கொண்டது. விளக்கெண்ணெயின் அடர்த்தி 961 கி.கி / மீ3. விளக்கெண்ணெய்யில் ஒரு துளி நீரை இடும்பொழுது, நீர்த்துளி மூழ்கும். ஆனால், நீரில் ஒரு துளி விளக்கெண்ணெய்யை இடும்பொழுது, அது மிதந்து நீரின் மீது ஒரு படலத்தை உருவாகும். எனினும், சில எண்ணெய் வகைகள் நீரை விட அதிக அடர்த்தி கொண்டவை.